Решение:
Предварительно прологарифмируем данную функцию:
,и продифференцируем обе части полученного равенства
.
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Основные методы интегрирования
Множество первообразных функции  имеет вид :
имеет вид :
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда
,
:
.
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Свойства определенного интеграла
Значение определенного интеграла |
принадлежит промежутку : |
Решение:
Если функция |
интегрируема на |
, |
и |
, то |
|
. |
|
|
|
Согласно свойств функции  наименьшее значение функции
наименьшее значение функции  на отрезке
на отрезке  достигается при
достигается при  и равно
и равно  , а наибольшее - при
, а наибольшее - при
и равно |
. |
Следовательно, |
, |
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Предел функции
Предел равен :
1
Решение:
Данный предел можно вычислить с использованием второго замечательного предела и его следствий вида . Тогда
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Область определения функции
Область определения функции  имеет вид :
имеет вид :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]
Решение:
Данная функция определена, если определен |
|
, то есть |
, и подкоренное |
выражение в знаменателе положительно, то есть |
|
|
. Решив неравенство |
, получаем |
. Для решения неравенства |
|
|
найдем предварительно |
корни уравнения |
|
, а именно |
и |
. Тогда методом интервалов |
можем получить, что |
|
. Следовательно, область определения данной |
функции будет иметь вид |
. |
|
|
|
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Частная производная  функции
функции  имеет вид :
имеет вид :
Решение:
При вычислении частной производной |
по переменной , переменную рассматриваем |
как постоянную величину. Тогда |
|
|
. |
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Приложения дифференциального исчисления ФОП
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]
Уравнение касательной к графику функции |
в его точке с абсциссой |
имеет вид : |
|
Решение:
Уравнение касательной к графику функции |
в его точке с абсциссой |
имеет |
вид |
. Вычислим последовательно |
|
|
, |
и |
|
|
. Тогда уравнение касательной примет вид |
|
, или |
. |
|
|
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Асимптоты графика функции
Вертикальная асимптота графика функции  задается уравнением вида :
задается уравнением вида :
Решение:
|
|
|
|
Прямая |
является вертикальной асимптотой графика функции |
, если эта |
функция определена в некоторой окрестности точки |
и |
, или |
. Вертикальные асимптоты обычно сопутствуют точкам разрыва второго рода. Определим точки разрыва данной функции. Это точки, в которых знаменатель равен
нулю. То есть |
, или |
, |
. |
|
Вычислим односторонние пределы |
функции |
в точке |
: |
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]
|
|
|
. |
Аналогично и |
, то есть прямая |
не является вертикальной |
асимптотой. |
|
в точке |
: |
Вычислим односторонние пределы функции |
|
, |
|
|
|
. |
|
|
Следовательно, прямая |
будет вертикальной асимптотой. |
|
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Сетевое планирование и управление
Матрица коэффициентов прямых затрат линейной статической модели Леонтьева имеет вид
. Тогда модель межотраслевого баланса представляется системой
уравнений :
Решение:
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]
Статическая линейная модель Леонтьева в матричной форме моделируется системой
, где 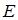 - единичная матрица. Следовательно, система линейных уравнений модели межотраслевого баланса имеет вид:
- единичная матрица. Следовательно, система линейных уравнений модели межотраслевого баланса имеет вид:
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Производственные функции
Производственная функция Леонтьевского типа с фиксированными пропорциями может иметь вид :
Решение:
Производственная функция Леонтьевского типа с фиксированными пропорциями определяется как  . Тогда правильным будет ответ:
. Тогда правильным будет ответ:  .
.
ЗАДАНИЕ N 21 сообщить об ошибке |
|
|
Тема: Функции полезности |
|
|
Функция полезности потребителя имеет вид |
, а бюджетное ограничение |
. |
Тогда оптимальный набор благ потребителя равен : |
|
|
, |
|
|
, |
|
|
, |
|
|
, |
|
|
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]
Решение:
Для вычисления оптимального набора благ потребителя необходимо решить оптимизационную задачу:
Воспользуемся методом множителей Лагранжа. Для этого построим функцию Лагранжа:
,
вычислим частные производные первого порядка и приравняем их к нулю:
Выразив из второго уравнения и подставив в первое, получим:
.
Тогда
 .
.
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Функции спроса и предложения |
|
Дана функция спроса |
, где - цена товара. Если равновесный объем спроса- |
предложения равен |
, то функция предложения |
может иметь вид : |
Решение:
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]
Вычислим равновесную цену спроса-предложения из условия |
, то есть |
. |
Решив это уравнение, получим . Тогда в качестве функции предложения можно взять возрастающую функцию, которая проходит через точку с координатами , . Этим условиям удовлетворяет, например, функция 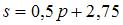 .
.
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Линейные операции над матрицами
Даны матрицы |
и |
. Если |
, то след матрицы равен : |
11
85
12
41
Решение:
Матрица находится следующим образом:
. След матрицы
равен сумме элементов главной диагонали:  .
.
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Системы линейных уравнений
Решение системы линейных уравнений  методом Крамера может иметь вид :
методом Крамера может иметь вид :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]
Решение:
Решение системы линейных уравнений с |
неизвестными определитель которой |
, |
находится по формулам Крамера |
, |
, |
, где |
- |
определитель, полученный из определителя системы заменой |
-го столбца столбцом |
|
свободных членов. То есть |
|
|
|
|
 ЗАДАНИЕ N 25 сообщить об ошибке
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Ранг матрицы |
|
Если минор второго порядка некоторой матрицы |
и все |
миноры более высокого порядка этой матрицы равны нулю, то ранг равен : |
|
2
3
0
1
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]


 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке имеет вид :
имеет вид :








 ЗАДАНИЕ N 25 сообщить об ошибке
ЗАДАНИЕ N 25 сообщить об ошибке

 наименьшее значение функции
наименьшее значение функции  на отрезке
на отрезке  достигается при
достигается при  и равно
и равно  , а наибольшее - при
, а наибольшее - при

 имеет вид :
имеет вид :
 функции
функции  имеет вид :
имеет вид :

 задается уравнением вида :
задается уравнением вида :
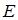 - единичная матрица. Следовательно, система линейных уравнений модели межотраслевого баланса имеет вид:
- единичная матрица. Следовательно, система линейных уравнений модели межотраслевого баланса имеет вид:
 . Тогда правильным будет ответ:
. Тогда правильным будет ответ:  .
. .
.
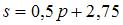 .
.
 .
.
 методом Крамера может иметь вид :
методом Крамера может иметь вид :