 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Точечные оценки параметров распределения
Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 8, 9, , 12. Если несмещенная оценка математического ожидания равна 10, то выборочная
дисперсия будет равна :
2,5
2,0
0
1,5
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Проверка статистических гипотез
Основная гипотеза имеет вид  . Тогда конкурирующей может являться гипотеза :
. Тогда конкурирующей может являться гипотеза :
Решение:
Конкурирующей (альтернативной) называют гипотезу, которая противоречит основной гипотезе. Условию  противоречит
противоречит  .
.
ЗАДАНИЕ N 25 сообщить об ошибке |
|
Тема: Статистическое распределение выборки |
|
Из генеральной совокупности извлечена выборка объема |
: |
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191841[05.04.2012 23:40:54]
34
81
47
33
 ЗАДАНИЕ N 26 сообщить об ошибке
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Характеристики вариационного ряда
Размах варьирования вариационного ряда -1, 0, 2, 3, 4, 5, 7, 8, 10, 12, 14 равен :
15
13
5
11
ЗАДАНИЕ N 27 сообщить об ошибке |
|
Тема: Линейные операции над матрицами |
|
Матрицы |
имеют одинаковую размерность. Если - единичная матрица того же размера, |
что и матрицы |
, и матрица |
, тогда верно равенство : |
 ЗАДАНИЕ N 28 сообщить об ошибке
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Системы линейных уравнений
Система |
совместна, если равно : |
1
2
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191841[05.04.2012 23:40:54]
- 1
- 2
Решение:
Система линейных уравнений совместна, если ранг основной матрицы системы равен рангу расширенной матрицы.
Расширенная матрица системы имеет вид |
Вычислим минор третьего порядка |
этой матрицы не содержащий элемент |
: |
|
Вычислим минор второго порядка этой матрицы не содержащий |
элемент : |
Ранг расширенной матрицы равен двум. Тогда ранг |
матрицы системы должен быть равен двум (определитель матрицы системы равен нулю, так как минор второго порядка не равный нулю существует). Из этого условия находим  :
:
Значит 
 ЗАДАНИЕ N 29 сообщить об ошибке
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Вычисление определителей
Разложение определителя |
по строке может иметь вид : |
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191841[05.04.2012 23:40:54]
 ЗАДАНИЕ N 30 сообщить об ошибке
ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Определение линейного пространства
Среди представленных множеств линейное пространство образует :

 множество всех векторов, принадлежащих пространству
множество всех векторов, принадлежащих пространству  множество всех векторов пространства , образующих острый угол с положительным
множество всех векторов пространства , образующих острый угол с положительным
направлением оси ординат  множество натуральных чисел
множество натуральных чисел
 множество всех отрицательных вещественных чисел
множество всех отрицательных вещественных чисел
 ЗАДАНИЕ N 31 сообщить об ошибке
ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Обратная матрица
Для матрицы
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191841[05.04.2012 23:40:54]
Преподаватель: Базайкина О.Л.
Специальность: 080104.65 - Экономика труда
Группа: ЭЭТ-091 Дисциплина: Математика
Идентификатор студента: Горбунова И.
Логин: 05ps511530
Начало тестирования: 2012-05-04 17:24:07 Завершение тестирования: 2012-05-04 17:31:33 Продолжительность тестирования: 7 мин. Заданий в тесте: 32 Кол-во правильно выполненных заданий: 4
Процент правильно выполненных заданий: 12 %
 ЗАДАНИЕ N 1 сообщить об ошибке
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Сетевое планирование и управление
Для сетевого графика, изображенного на рисунке,
длина критического пути равна 42. Тогда значение параметра равно :
8
18
0
42
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Линейное программирование: графическое задание области допустимых решений
Область допустимых решений OABC задачи линейного программирования имеет вид:
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]
Тогда максимальное значение функции |
достигается в точке : |
B |
|
D |
|
A |
|
C |
|
Решение:
Построим линию уровня и градиент целевой функции
. Тогда целевая функция будет принимать наибольшее значение в
точке <выхода> линии уровня из области допустимых решений в направлении градиента.
Из рисунка видно, что точкой максимума будет точка B как точка <выхода> линии уровня  из области допустимых решений в направлении градиента.
из области допустимых решений в направлении градиента.
 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]
Тема: Теория игр: игры с природой
Матрица рисков в игре с природой имеет вид:
Тогда средний риск игрока по критерию Байеса относительно рисков будет равен :
2,4
5
2
4,6
Решение:
Определим предварительно неизвестную вероятность |
и вычислим средние |
риски игрока: |
|
, |
|
, |
|
, |
|
. |
|
Тогда наименьший средний риск игрока будет равен 2,4. |
|
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Транспортная задача
В транспортной задаче распределение поставок задано таблицей:
Тогда значение потенциала  будет равно :
будет равно :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]
- 2
0
2
4
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Характеристики вариационного ряда
Мода вариационного ряда 3, 4, 5, 5, 5, 6, 6, 8, 10, 10, 11, 11, 11, 11, 13 равна :
11
13
15
10
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Интервальные оценки параметров распределения
Точечная оценка математического ожидания нормально распределенного количественного признака равна 0,4. Тогда его интервальная оценка может иметь вид :
Решение:
Интервальная оценка математического ожидания нормально распределенного количественного признака симметрична относительно его точечной оценки. Таким свойством обладает интервал 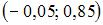 .
.
ЗАДАНИЕ N 7 сообщить об ошибке |
|
Тема: Статистическое распределение выборки |
|
Из генеральной совокупности извлечена выборка объема |
: |
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]
Тогда значение  равно :
равно :
34
81
47
33
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Проверка статистических гипотез
Основная гипотеза имеет вид  . Тогда конкурирующей может являться гипотеза :
. Тогда конкурирующей может являться гипотеза :
Решение:
Конкурирующей (альтернативной) называют гипотезу, которая противоречит основной гипотезе. Условию  противоречит
противоречит  .
.
ЗАДАНИЕ N 9 сообщить об ошибке |
|
|
Тема: Элементы корреляционного анализа |
|
|
Выборочное уравнение прямой линии регрессии на |
имеет вид |
, а выборочные |
средние квадратические отклонения равны: |
. Тогда выборочный коэффициент |
корреляции |
равен : |
|
|
Решение:
Выборочный коэффициент корреляции можно вычислить из соотношения .
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]
Тогда  .
.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Точечные оценки параметров распределения
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 3,6; 3,8; 4,3. Тогда несмещенная оценка дисперсии равна :
0,13
0,065
3,9
0,7
Решение:
Несмещенная оценка дисперсии вычисляется по формуле:
, где |
. Вычислив предварительно |
, |
получаем |
|
|
|
. |
|
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Производные первого порядка
Производная функции  равна :
равна :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511530[11.05.2012 0:05:04]


 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке . Тогда конкурирующей может являться гипотеза :
. Тогда конкурирующей может являться гипотеза : противоречит
противоречит  .
.


 ЗАДАНИЕ N 30 сообщить об ошибке
ЗАДАНИЕ N 30 сообщить об ошибке
 множество всех векторов, принадлежащих пространству
множество всех векторов, принадлежащих пространству  множество всех векторов пространства , образующих острый угол с положительным
множество всех векторов пространства , образующих острый угол с положительным множество натуральных чисел
множество натуральных чисел множество всех отрицательных вещественных чисел
множество всех отрицательных вещественных чисел ЗАДАНИЕ N 31 сообщить об ошибке
ЗАДАНИЕ N 31 сообщить об ошибке








 :
:



 из области допустимых решений в направлении градиента.
из области допустимых решений в направлении градиента.

 будет равно :
будет равно :

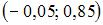 .
. равно :
равно :
 . Тогда конкурирующей может являться гипотеза :
. Тогда конкурирующей может являться гипотеза : противоречит
противоречит  .
. .
.

 равна :
равна :