3
.pdf
Тогда значение a равно …
38 
39
76 
37
Решение:
Так как объем выборки вычисляется как 
, где 
, то 
.
Преподаватель: Базайкина О.Л.
Специальность: 080104.65 - Экономика труда
Группа: ЭЭТ-091 Дисциплина: Математика
Идентификатор студента: Сапегина К.
Логин: 05ps28789
Начало тестирования: 2012-03-06 11:23:41 Завершение тестирования: 2012-03-06 12:14:36 Продолжительность тестирования: 50 мин. Заданий в тесте: 32 Кол-во правильно выполненных заданий: 20
Процент правильно выполненных заданий: 62 %
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии 
на 
имеет вид
. Тогда выборочное среднее признака 
равно …
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Точечные оценки параметров распределения
Проведено четыре измерения (без систематических ошибок) некоторой
случайной величины (в мм): 8, 9, 
, 12. Если несмещенная оценка математического ожидания равна 10, то выборочная дисперсия будет равна …
2,5 
2,0
0 
1,5
Решение:
Вычислим предварительно значение 
. Так как несмещенная оценка
математического ожидания вычисляется по формуле: 
, то
. Следовательно, 
.
Для вычисления выборочной дисперсии применим формулу 
.
Тогда 
.
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема 
, гистограмма частот которой имеет вид:
Тогда значение a равно …
38 
39
76 
37
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Интервальные оценки параметров распределения
Дан доверительный интервал 
для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении надежности (доверительной вероятности) оценки доверительный интервал может принять вид …
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Проверка статистических гипотез
Соотношением вида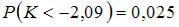 
можно определить …
левостороннюю критическую область 
правостороннюю критическую область
двустороннюю критическую область 
область принятия гипотезы
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Характеристики вариационного ряда
Размах варьирования вариационного ряда 2, 3, 4, 5, 5, 7, 9, 10, 12, 14, 
равен
15. Тогда значение 
равно … 
17
13
15 
11
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Сетевое планирование и управление
Сетевой график изображен на рисунке
Тогда полный резерв времени работы |
равен … |
3 
8
0 
11
Решение:
Выделим полные пути: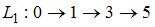 
,
,
,
, вычислим их длины: 
, 
, 
,
. Тогда критическим будет путь 
с наибольшей длиной 
. Полный резерв времени работы 
равен разности между 
и наибольшей длиной (
) пути, проходящей
через эту работу. Следовательно, 
.
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Транспортная задача
В транспортных задачах A)
B)
оптимальное распределение поставок …
имеет задача B 
имеет задача A
имеет и задача A и задача B 
не имеет ни одна из задач
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Теория игр: игры с природой
Дерево решений в игре с природой имеет вид:
Тогда ожидаемая денежная оценка по критерию Байеса будет равна …
2150 
12500
– 800 
3787,5
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Линейное программирование: графическое задание области допустимых решений
Область допустимых решений ABCDE задачи линейного программирования имеет вид:
Тогда максимальное значение функции 
достигается в точке …
D
C
B
точки максимума не существует
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Линейные операции над матрицами
Матрицы 
имеют одинаковую размерность. Если 
– единичная матрица
того же размера, что и матрицы 
, и матрица 
, тогда верно равенство …
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Обратная матрица
Для матрицы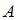 
существует обратная, если ее определитель …
=0
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Системы линейных уравнений
Решение системы линейных уравнений 
методом Крамера может иметь вид …
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Определение линейного пространства
Среди представленных множеств линейное пространство не образует …
множество всех матриц размерностью m×n, содержащих только положительные числа
множество всех векторов, принадлежащих пространству 
множество всех матриц размерностью m×n
множество всех векторов, принадлежащих пространству 
Решение:
Множество 
образует линейное пространство, если для любых 2-х его
элементов 
определены операции сложения 
и умножения на действительное число 
; 
со свойствами:
1. 
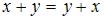
2. 
3. 
4. 
5. 
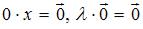
6. 
При проверке аксиом получим, что множество всех матриц размерностью m´n, содержащих только положительные числа, не образуют линейного пространства, т.к. умножение на отрицательное число получаем матрицу с отрицательными числами и не выполняется шестая аксиома.
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Вычисление определителей
Разложение определителя 
по строке может иметь вид …
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Ранг матрицы
Ранг матрицы 
равен …
1 
2
3 
0
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина 
задана законом распределения вероятностей:
Тогда значения a и b могут быть равны …
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Числовые характеристики случайных величин
Дискретная случайная величина X задана законом распределения вероятностей:
Тогда ее дисперсия равна …
7,56 
3,2
3,36 
6,0
Решение:
Дисперсию дискретной случайной величины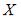 
можно вычислить по формуле
. Тогда
.
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Вероятность поражения цели первым стрелком равна 0,9, а вторым – 0,85. Оба стрелка стреляют одновременно. Тогда вероятность поражения цели, равна …
0,985 
0,775
0,875 
1,75
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Определение вероятности
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – семь, а разность – три, равна …
0
Решение:
Для вычисления события 
(сумма выпавших очков будет равна семи, а
разность – трем) воспользуемся формулой 
, где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае
возможны 
элементарных исходов испытания, из которых благоприятствующими являются исходы вида 
и 
, то есть 
.
Следовательно, 
.
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Сетевое планирование и управление