3

Значение выборочного коэффициента корреляции, во-первых, принадлежит промежутку

, а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение .

ЗАДАНИЕ N 5 сообщить об ошибке

Тема: Интервальные оценки параметров распределения

Точечная оценка математического ожидания нормально распределенного количественного признака равна 0,4. Тогда его интервальная оценка может иметь вид :

Решение:

Интервальная оценка математического ожидания нормально распределенного количественного признака симметрична относительно его точечной оценки. Таким свойством обладает интервал .

Тогда относительная частота варианты равна :

0,25

0,75

0,24

0,04

ЗАДАНИЕ N 7 сообщить об ошибке

Тема: Теоремы сложения и умножения вероятностей

http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191840[05.04.2012 23:48:10]

Из урны, в которой лежат 3 белых и 7 черных шара, наудачу по одному извлекают два шара без

возвращения. Тогда вероятность того, что только один из извлеченных шаров будет белым, равна

:

Решение:

Введем обозначения событий: - k-ый вынутый шар будет белым, A - только один из

.

ЗАДАНИЕ N 8 сообщить об ошибке

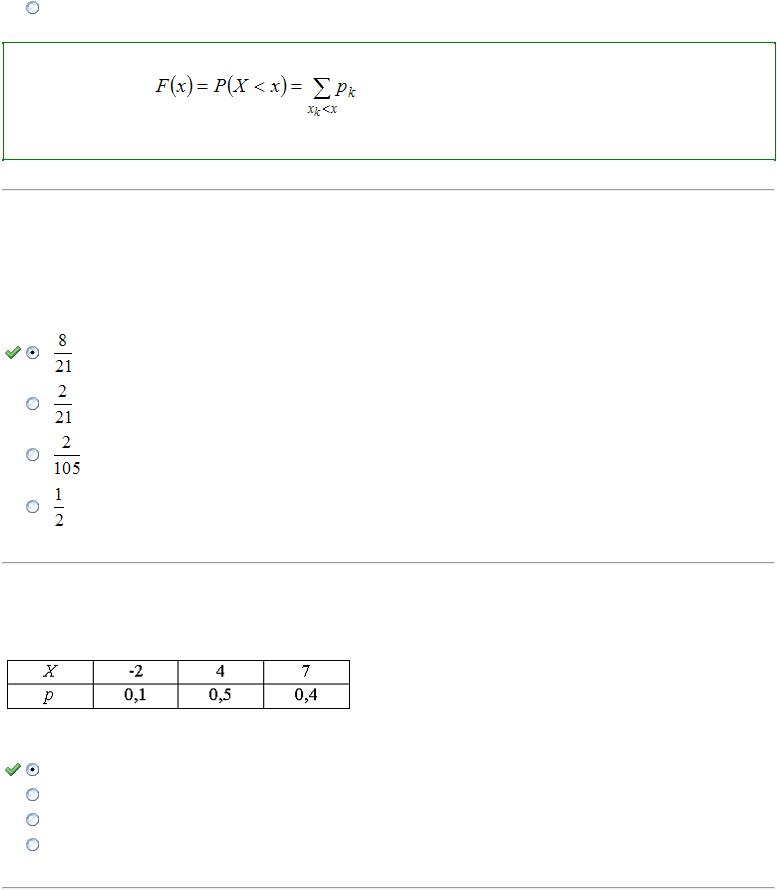
Тема: Законы распределения вероятностей дискретных случайных величин

Для дискретной случайной величины :

функция распределения вероятностей имеет вид:

Тогда значение параметра может быть равно :

0,655

1

0,25

http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191840[05.04.2012 23:48:10]

0,45

Решение:

По определению . Следовательно, и . Этим условиям удовлетворяет, например, значение .

ЗАДАНИЕ N 9 сообщить об ошибке

Тема: Определение вероятности

Из урны, в которой находятся 6 белых шаров и 4 черных шара, вынимают одновременно 4 шара. Тогда вероятность того, что среди отобранных 3 шара будут белыми, равна :

ЗАДАНИЕ N 10 сообщить об ошибке

Тема: Числовые характеристики случайных величин

Дискретная случайная величина X задана законом распределения вероятностей:

Тогда ее математическое ожидание равно :

4,6

5,0

3,0

4,9

ЗАДАНИЕ N 11 сообщить об ошибке

Тема: Функции спроса и предложения

http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191840[05.04.2012 23:48:10]

, и <точка> равновесия . Если значение параметра

уменьшится, то :

равновесная цена и равновесный объем спроса-предложения уменьшатся

равновесная цена и равновесный объем спроса-предложения увеличатся

равновесная цена спроса-предложения уменьшится, а равновесный объем увеличится равновесная цена спроса-предложения увеличится, а равновесный объем уменьшится

ЗАДАНИЕ N 12 сообщить об ошибке

Тема: Производственные функции

Производственная функция с постоянной эластичностью замены (CES) может иметь вид :

ЗАДАНИЕ N 13 сообщить об ошибке

Тема: Сетевое планирование и управление

Статическая линейная модель Леонтьева многоотраслевой экономики продуктивна. Тогда матрица коэффициентов прямых затрат может иметь вид :

http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191840[05.04.2012 23:48:10]

ЗАДАНИЕ N 15 сообщить об ошибке

Тема: Производные первого порядка

порядка функции по переменной имеет вид :

Решение:

.

ЗАДАНИЕ N 16 сообщить об ошибке

Тема: Предел функции

Предел равен :

0

1

Решение:

http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191840[05.04.2012 23:48:10]

Для раскрытия этой неопределенности умножим числитель и знаменатель на выражение, сопряженное числителю, то есть на :

ЗАДАНИЕ N 17 сообщить об ошибке

Тема: Дифференциальное исчисление ФНП

Значение частной производной функции в точке равно :

Решение:

http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191840[05.04.2012 23:48:10]

Решение:

То есть , следовательно, .

ЗАДАНИЕ N 19 сообщить об ошибке

Тема: Основные методы интегрирования

Множество первообразных функции имеет вид :

Решение:

http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191840[05.04.2012 23:48:10]

Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой

функции. Тогда

.

ЗАДАНИЕ N 20 сообщить об ошибке

Решение:

http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191840[05.04.2012 23:48:10]

ЗАДАНИЕ N 22 сообщить об ошибке

Тема: Асимптоты графика функции

Вертикальная асимптота графика функции задается уравнением вида :

ЗАДАНИЕ N 23 сообщить об ошибке

Тема: Линейные операции над матрицами

http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191840[05.04.2012 23:48:10]