3
.pdf
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина 
задана законом распределения вероятностей:
Тогда вероятность |
равна … |
0,5 
0,8
0,7 
0,1
Решение:
.
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Определение вероятности
В круг радиуса 8 помещен меньший круг радиуса 5. Тогда вероятность того, что точка, наудачу брошенная в больший круг, попадет также и в меньший круг, равна …
Решение:
Для вычисления вероятности искомого события воспользуемся формулой 
, где 
– площадь меньшего круга, а 
– площадь большего круга. Следовательно, 
.
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
В электрическую цепь последовательно включены два элемента, работающие независимо друг от друга. Вероятности отказов элементов равны соответственно 0,1 и 0,15. Тогда вероятность того, что тока в цепи не будет, равна …
0,235 
0,765
0,22 
0,015
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Линейное программирование: графическое задание области допустимых решений
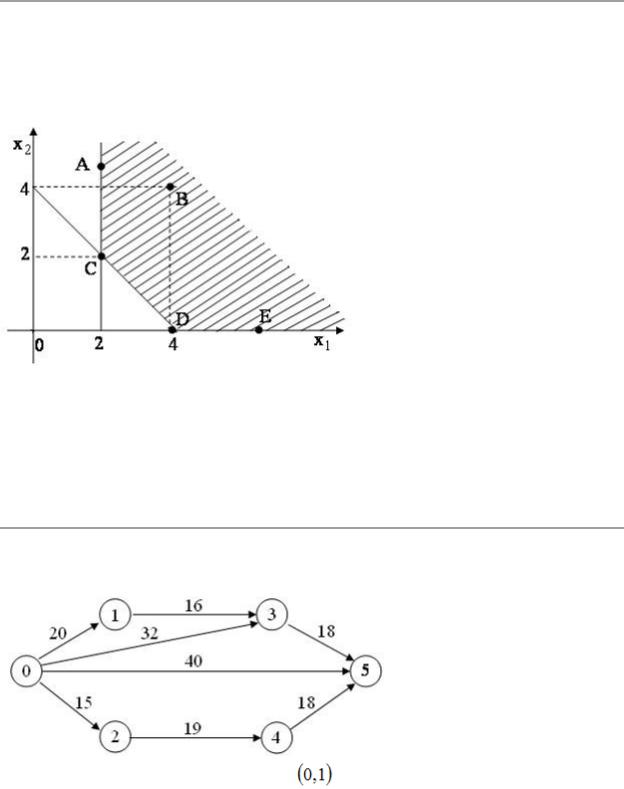
Область допустимых решений ABCDE задачи линейного программирования имеет вид:
Тогда максимальное значение функции 
равно …
– 4
– 12
0 
4
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Сетевое планирование и управление
Сетевой график изображен на рисунке
Тогда полный резерв времени работы |
равен … |
0 
4
34 
20
Решение:
Выделим полные пути: 
, 
, 
, 
,
вычислим их длины: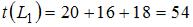 
, 
, 
, 
. Тогда критическим будет путь 
с
наибольшей длиной 
. Так как работа 
располагается на критическом пути, то ее резервы равны нулю, то есть 
.
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Теория игр: игры с природой
Матрица выигрышей в игре с природой имеет вид:
Тогда соответствующая ей матрица рисков будет иметь вид …
Решение:
Определим предварительно показатели благоприятности
и 
и вычислим соответствующие риски игрока, как разности между показателями благоприятности и соответствующими элементами матрицы выигрышей:
, 
, 
, 
,
, 
, 
, 
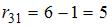. Тогда матрица рисков примет вид:
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Транспортная задача
Транспортная задача
будет закрытой, если …
, 
, 
, 
, 
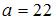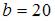
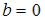
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Область определения функции
Область определения вида 
соответствует функции …
Решение:
Решим уравнение 
, то есть 
и 
. Тогда область определения:
функции 
имеет вид 
; функции 
имеет вид 
; функции 
имеет вид 
; функции 
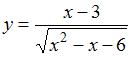имеет вид 
.
То есть правильным будет ответ: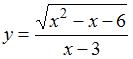 
.
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Асимптоты графика функции
Вертикальная асимптота графика функции 
задается уравнением вида …
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Основные методы интегрирования
Множество первообразных функции 
имеет вид …
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда
.
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Свойства определенного интеграла
Если функция 
непрерывна на отрезке 
, то интеграл 
можно представить в виде …
Решение:
Если функция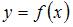 
непрерывна на отрезке 
и 
, то справедливо следующее свойство определенного интеграла:
.
Тогда 
.
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Частная производная 
функции 
имеет вид …
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Приложения дифференциального исчисления ФОП
Наибольшее значение функции
на отрезке 
равно …
– 1
0
Решение:
Вычислим производную первого порядка
и решим уравнение 
, а
именно 
. Тогда 
. Так как 
, а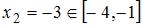 
, то вычислим
, 
, 
. Тогда наибольшее значение данной функции равно 
.
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Предел функции
Предел 
равен …
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Производные первого порядка
Производная функции 
равна …
Решение:
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Проверка статистических гипотез
Соотношением вида 
можно определить …
левостороннюю критическую область 
правостороннюю критическую область
двустороннюю критическую область 
область принятия гипотезы
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Характеристики вариационного ряда
Медиана вариационного ряда 11, 13, 13, 14, 15, 
, 18, 19, 21, 24, 25, 25 равна 17. Тогда значение варианты 
равно …
16 
17
18 
15
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Интервальные оценки параметров распределения
Дан доверительный интервал 
для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении объема выборки этот доверительный интервал может принять вид
…
Решение:
Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде
симметричного интервала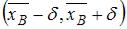 
, где точечная оценка
математического ожидания 
, а точность оценки 
. В случае
увеличения объема выборки точность оценки улучшается, то есть значение 
будет меньше 1,14.
ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Элементы корреляционного анализа
При построении выборочного уравнения парной регрессии вычислены выборочный коэффициент корреляции 
и выборочные средние
квадратические отклонения 
. Тогда выборочный коэффициент регрессии Y на X равен …
ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Точечные оценки параметров распределения
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна …
11,25 
19,5
15 
21,25
Решение:
Выборочная дисперсия вычисляется по формуле
, где 
. Вычислив предварительно
, получаем
.
ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема 
, гистограмма частот которой имеет вид: