3
.pdf
Решение:
В оптимальном распределении сумма потенциалов для свободных клеток
должна быть меньше или равна тарифу: 
. Этим условиям соответствует распределение, имеющее вид:
Действительно, 
, 
, 
,
.
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Теория игр: игры с природой
Матрица выигрышей в игре с природой имеет вид:
Тогда соответствующая ей матрица рисков будет иметь вид …
Решение:
Определим предварительно показатели благоприятности
и 
и вычислим соответствующие риски игрока, как разности между показателями благоприятности и соответствующими элементами матрицы выигрышей:
, 
, 
, 
,
, 
, 
, 
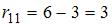. Тогда матрица рисков примет вид:
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Сетевое планирование и управление
Для сетевого графика, изображенного на рисунке,
длина критического пути равна 42. Тогда значение параметра 
равно …
8 
18
0 
42
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Вычисление определителей
Корень уравнения 
равен …
– 3 
0
3
– 9
Решение:
Определитель третьего порядка можно вычислить, например, разложением по элементам первой строки:
. По условию задачи определитель должен равняться 
, то есть 
. Следовательно, 
.
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Обратная матрица
Обратной для матрицы 
является матрица …
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Определение линейного пространства
На линейном пространстве 
задана операция …
, для любых 
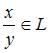, для любых 
, для любых 
, для любых 
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Ранг матрицы
Ранг матрицы 
равен …
1 
2
3 
0
Решение:
Ранг матрицы не изменяется при её элементарных преобразованиях, поэтому столбцы и строки матрицы можно менять местами, складывать, вычитать, умножать на числа, отличные от 0, с целью приведения её к диагональному виду. Число ненулевых элементов главной диагонали будет равно рангу
матрицы. В данном случае сначала удобнее обнулить элементы первого столбца
под первым элементом первой строки и т.д.: 
Только один диагональный элемент ненулевой, поэтому ранг матрицы 
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Линейные операции над матрицами
Дана матрица 
. Если матрица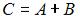 
является диагональной, то матрица 
может иметь вид …
Решение:
При сложении или вычитании матриц одинаковой размерности соответствующие элементы матриц складываются или вычитаются друг из друга.
Так как матрица C является диагональной, то она должна иметь вид:
.
Тогда
.
Например,
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Системы линейных уравнений
Базисное решение системы 
может иметь вид …
Решение:
По методу Гаусса приведем матрицу системы с помощью элементарных преобразований строк к трапецеидальной или треугольной форме. Запишем
расширенную матрицу системы и преобразуем ее: 
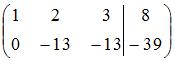
. Следовательно, система может быть
записана в виде 
, где 
– свободная переменная, а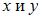 
– базисные. Общее решение будет иметь вид:
. Базисным решением называется всякое решение системы, в котором свободные переменные имеют нулевые значения. Значит 
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина 
задана законом распределения вероятностей:
Тогда значения a и b могут быть равны …
Решение:
Так как сумма вероятностей возможных значений 
равна 1, то 
. Этому условию удовлетворяет ответ:
.
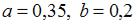ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Определение вероятности
Из урны, в которой находятся 6 белых шаров и 4 черных шара, вынимают одновременно 4 шара. Тогда вероятность того, что среди отобранных 3 шара будут белыми, равна …
Решение:
Для вычисления события 
(среди отобранных шаров три шара будут белыми)
воспользуемся формулой 
, где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно
извлечь четыре шара из десяти имеющихся, то есть 
. А общее число благоприятствующих исходов равно числу способов, которыми можно извлечь
три белых шара из шести и один черный шар из четырех, то есть 
.
Следовательно, 
ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Числовые характеристики случайных величин
Математическое ожидание дискретной случайной величины 
, заданной законом распределения вероятностей:
равно 4,4. Тогда значение вероятности 
равно …
0,7 
0,3
0,6 
0,4
Решение:
Математическое ожидание дискретной случайной величины вычисляется по
формуле 
. Тогда 
. А с учетом условия 
получаем систему уравнений:
решение которой имеет вид: 
, 
.
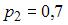ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
В электрическую цепь последовательно включены два элемента, работающие независимо друг от друга. Вероятности отказов элементов равны соответственно 0,1 и 0,15. Тогда вероятность того, что тока в цепи не будет, равна …
0,235 
0,765
0,22
0,015
Решение:
Введем обозначения событий: 
(откажет k-ый элемент), 
(тока в цепи не будет).
Тогда
Преподаватель: Базайкина О.Л.
Специальность: 080104.65 - Экономика труда
Группа: ЭЭТ-091 Дисциплина: Математика
Идентификатор студента: Макушенко Р.
Логин: 05ps28812
Начало тестирования: 2012-03-10 08:49:21 Завершение тестирования: 2012-03-10 09:23:38 Продолжительность тестирования: 34 мин. Заданий в тесте: 32 Кол-во правильно выполненных заданий: 10
Процент правильно выполненных заданий: 31 %
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Линейное программирование: графическое задание области допустимых решений
Область допустимых решений ABCDE задачи линейного программирования имеет вид:
Тогда минимальное значение функции 
равно …
6 
0
18
12
Решение:
Построим линию уровня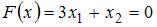 
и градиент целевой функции
. Тогда целевая функция будет принимать наименьшее значение в точке «входа» линии уровня в область допустимых
решений в направлении градиента. Это точка 
.
Следовательно, |
. |
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Теория игр: игры с природой
Матрица выигрышей в игре с природой имеет вид:
Тогда оптимальной по критерию пессимизма-оптимизма Гурвица относительно выигрышей с показателем пессимизма 
будет стратегия …
Решение:
Показателем эффективности стратегии 
по этому критерию является величина 
, а оптимальной будет стратегия, которой соответствует: 
. Вычислим значения 
:
,
,