3

4

Решение:

Сумма потенциалов для занятых клеток должна быть равна тарифу. Следовательно, , то есть . , то есть .

, то есть .

ЗАДАНИЕ N 13 сообщить об ошибке

Тема: Производственные функции

Задана производственная функция . Тогда предельный продукт капитала при , равен …

Решение:

Предельный продукт капитала вычисляется по формуле . Тогда

. А в точке

.

ЗАДАНИЕ N 14 сообщить об ошибке

Тема: Сетевое планирование и управление

В линейной статической модели Леонтьева объемы конечного продукта

представлены вектором , объемы валовых выпусков – вектором . Тогда объемы промежуточной продукции можно представить матрицей …

Решение:

В модели Леонтьева валовой выпуск , конечный продукт и промежуточное потребление связаны системой уравнений:

Тогда объемы промежуточной продукции можно представить матрицей:

.

ЗАДАНИЕ N 15 сообщить об ошибке

Тема: Функции спроса и предложения

Дана функция предложения , где – цена товара. Если равновесный объем спроса-предложения равен , то функция спроса

может иметь вид …

Решение:

Вычислим равновесную цену спроса-предложения из условия , то есть

. Решив это уравнение, получим . Тогда в качестве функции спроса можно взять убывающую функцию, которая проходит через точку с координатами , . Этим условиям удовлетворяет,

например, функция .

ЗАДАНИЕ N 16 сообщить об ошибке

Тема: Функции полезности

В теории потребления предполагается, что функция полезности потребителя обладает свойством …

ЗАДАНИЕ N 17 сообщить об ошибке

Тема: Законы распределения вероятностей дискретных случайных величин

Для дискретной случайной величины :

функция распределения вероятностей имеет вид:

Тогда значение параметра может быть равно …

0,7

1

0,85

0,6

ЗАДАНИЕ N 18 сообщить об ошибке

Тема: Теоремы сложения и умножения вероятностей

В урну, в которой лежат 6 белых и 5 черных шаров добавляют два черных шара. После этого наудачу по одному извлекают три шара без возвращения. Тогда вероятность того, что хотя бы один шар будет белым, равна …

Решение:

Введем обозначения событий: – -ый вынутый шар будет белым, A – хотя бы один шар будет белым. Тогда , где – -ый

вынутый шар не будет белым. Так как по условию задачи события , и 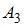зависимы, то

.

ЗАДАНИЕ N 19 сообщить об ошибке

Тема: Числовые характеристики случайных величин

Дискретная случайная величина X задана законом распределения вероятностей:

Тогда ее математическое ожидание равно …

4,6

5,0

3,0

4,9

Решение:

Математическое ожидание дискретной случайной величины вычисляется по формуле . Тогда .

ЗАДАНИЕ N 20 сообщить об ошибке

Тема: Определение вероятности

При наборе телефонного номера абонент забыл две последние цифры и набрал их наудачу, помня только, что эти цифры нечетные и разные. Тогда вероятность того, что номер набран правильно, равна …

Решение:

Для вычисления события (сумма выпавших очков будет равна десяти)

воспользуемся формулой , где – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A.

Вычислим общее число элементарных исходов испытания. Предпоследний

номер можно набрать пятью способами , а последний – четырьмя, так как набранные цифры должны быть разными. Тогда по правилу произведения

28

63

42

35

Решение:

Вычислим предварительно относительную частоту варианты как . Тогда из определения относительной

частоты , получаем, что .

ЗАДАНИЕ N 23 сообщить об ошибке

Тема: Точечные оценки параметров распределения

Из генеральной совокупности извлечена выборка объема :

Тогда выборочное среднее квадратическое отклонение равно …

Решение:

Выборочное среднее квадратическое отклонение вычисляется как , где

. Тогда

,

и

ЗАДАНИЕ N 24 сообщить об ошибке

Тема: Интервальные оценки параметров распределения

Точечная оценка вероятности биномиально распределенного количественного признака равна 0,38. Тогда его интервальная оценка может иметь вид …