
3. Подобие объектов управления
.pdf3 ИССЛЕДОВАНИЕ СОВМЕСТНОГО ПОДОБИЯ ОБЪЕКТОВ
УПРАВЛЕНИЯ И ВНЕШНИХ ВОЗДЕЙСТВИЙ
Значения показателей эффективности систем управления любой структуры существенно зависят как от динамических свойств каналов преобразования изменений входных воздействий управляемых объектов, так и от характеристик самих этих воздействий, в том числе и неконтролируемых возмущений. Поэтому одной из важных задач подобия систем управления, как это отмечено в [1], является определение совместного подобия входных воздействий и динамических свойств каналов их преобразования в объекте управления. В [1] сформулированы утверждения 3 и 4, которые определяют условия такого подобия, при этом неконтролируемые возмущения рекомендуется приводить к одному из управляющих входов. Условие совместного подобия объектов и входных, в том числе и неконтролируемых, воздействий на конечном интервале времени сформулированы в виде соотношений, отражающих в общем виде приближенное равенство эффектов влияния изменений входных воздействий на изменения выходных воздействий объекта управления.
Поэтому важными являются исследования, направленные на выявление условий, при которых в зависимости от конкретных характеристик и свойств внешних воздействий и каналов их преобразования выполняется такое совместное подобие.
Далее будет приведена постановка задачи исследования совместного подобия объектов управления и внешних воздействий, схема и результаты ее решения,
полученные с помощью аналитического и численного методов. Основные условия постановки задачи были сформулированы таким образом, чтобы ее решение можно было бы получить известными аналитическими и численными методами. Во-первых,
полученный результат аналитического решения может отражать реально существующие взаимосвязи между характеристиками непосредственно или косвенно оцененных внешних воздействий и каналов их преобразования в объекте, что в дальнейшем может помочь выбрать структуру показателя (критерия) совместного

подобия объекта и входных воздействий. Во-вторых, он (результат) может быть использован при проверке качества функционирования алгоритма численного решения поставленной задачи.
3.1 Постановка задачи исследования подобия объектов, представленных
моделью инерционного звена первого порядка с запаздыванием
Дано:
1. Структура объекта управления
uпр(s) |
u(s) |
|
|
|
y(s) |
|
|
|
|
||||
uо(s) |
+ |
|
|
|
||
|
|
|
|
|||
|
φτ(s) |
|
φо(s) |
|
||
|
+ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Рисунок 3.1 – Структура объекта управления |
||||||
|
|
y(s) o u(s) ; |
(3.1) |
|||
u(s) uo |
(s) uпр |
(s); |
(3.2) |
|
|
|
На рисунке 3.1 приняты следующие обозначения:
uo(s) – опорный уровень управляющего воздействия;
uпр(s) – приведенное к управляющему входу эквивалентное возмущение; u(s) – управляющее воздействие;
y(s) – выходное воздействие объекта управления;
φτ(s) – оператор звена запаздывания;
φо(s) – оператор объекта управления без запаздывания.
2. Математическая модель объекта управления, представленная в операторной форме с помощью последовательно соединенных инерционного звена первого
порядка и звена запаздывания: |
|
|
|
|
(s) |
k |
e s |
|
|
|
|
|
||
Ts 1 |
|
|||
|
, |
(3.3) |
||
|
|
|
||
где k – коэффициент передачи объекта, T – время инерции, τ – запаздывание.

3. Приведенные к управляющему входу объекта управления воздействия представляют собой стационарный временной ряд с экспоненциально спадающей нормированной автокорреляционной функцией (АКФ)
rпр ( ) пр2 e ,
где пр2 – дисперсия приведенного возмущения, – коэффициент спада АКФ,
время сдвига между сечениями ряда приведенных возмущений.
4.Условием подобия является неравенство следующего вида:
yн1 yн2 0,05
(3.4)
θ –
(3.5)
где yн1 и yн2 – нормированные значения среднеквадратических отклонений выходных переменных объектов, подобие которых оценивается.
Среднеквадратическое отклонение (СКО) выходной переменной объекта как
оценка эффектов влияния входных воздействий на выходные для численных исследований равна:
2 = |
1 |
|
|
|
|
√(( ) − ̅)2 |
(3.6) |
||||
|
|||||
|
−1 |
|
|||
|
|
||||
5. Начальные условия |
|
|
|
|
|
y(0) = 0; u0(0) = 0; uпр(0) = 0; |
(3.7) |
||||
6. Ограничение по времени спада θs нормированной АКФ приведенного |
|||||
возмущения определяется соотношением |
|
||||
θs= θ при r(θ) = 0,2. |
(3.8) |
||||
Требуется
1.Сформировать условия или возможный показатель (критерий) для оценки подобия.
2.Проверить полученный показатель на натурно-модельных данных.
3.Исследовать влияние изменений характеристик Т (постоянная времени инерции), α (коэффициент спада АКФ), σпр (дисперсия приведенного возмущения), ш
(запаздывание), k (коэффициент передачи объекта) на изменения СКО выходного
воздействия.
Решение поставленной задачи
Для линейного объекта дисперсия выходного воздействия y2 оценивается следующим выражением [15]
y2 |
1 |
Gyy ( )d , |
|
|
2 |
|
(3.9) |
||
|
|
|
||
|
|
|
|
|
спектр мощности выходного воздействия G уу ( ) определяется как |
|
|||
Gyy ( ) W ( j ) 2 |
Gпр ( ), |
(3.10) |
||
где Gпр ( ) – спектр мощности приведенного |
возмущения, W ( j ) |
– частотная |
||
характеристика объекта управления.
Оценивания спектр мощности приведенного возмущения Gпр ( ) с учетом (3.4),
а частотную характеристику объекта управления W ( j ) с учетом (3.3), получим с использованием (3.9) и (3.10) следующее выражение для дисперсии выходных
воздействий:
y2 |
|
k 2 пр2 |
|
||
|
|
|
|||
1 T . |
(3.11) |
||||
|
|
||||
Для вычисления значений |
дисперсии (3.11) использовали |
систему |
|||
компьютерной алгебры MathCAD. Вычисления проводили при выполнении следующих условий:
1) значения характеристик динамического ряда приведенных ко входу
возмущений находились в пределах: 1 пр 30 ; 0,01 0,1. Значение параметра σпр
меняли с шагом Δσпр = 1; α – с шагом Δα = 0,01; 2) диапазон исследования характеристик объекта:
1 T 500 , с шагом дискретизации |
T = 1; |
|
|
||
|
|
|
1 |
|
|
1 k 10 , с шагом дискретизации |
k = 1; |
|
= |
|
. |
|
|
||||
|
|
|
10 |
||
Для реализации численных исследований |
использовали моделирующий |
||||
комплекс [11] и алгоритм формирования случайных сигналов с коррекцией по обратной связи [12]. При этом кроме условий 1) и 2) выполняли дополнительно следующие условия:
3)интервал моделирования I = 25000 c. Шаг дискретизации по времени ∆t=1c;
4)заданная точность отклонения результатов аналитических уа и численных
уч решений должна быть не более 5%, т.е.
|
y |
|
а ч |
0,05 |
|
|
|
|
y |
y |
|
(3.12) |
|
|
|
|
|
|
|
|
Анализ результатов
В процессе исследовании были проведены серии аналитических расчетов и численных экспериментов при зафиксированных условиях (1)−(4). Результаты
аналитических расчетов уа сравнивались с результатами численных исследований
уч по выражению (3.12). Обобщенные результаты исследования отражены в таблице
3.1, где приведены лишь минимальные |
ум ин |
усред |
, срединные |
и максимальные |
ум акс значения отклонений (3.12) для условий, приведенных в каждой строке левого столбца этой таблицы.
Таблица 3.1 – Отклонения между аналитическими и численными значениями для модели объекта в виде инерционного звена первого порядка
Диапазон изменения параметров |
мин |
сред |
макс |
|
|
|
y ,% |
y , % |
y , % |
|
|
|
|
|
1 пр 30 |
, Δσпр = 1 |
1,04 |
1,26 |
2,13 |
|
||||
|
|
|
|
|
0,01 0,1, Δα = 0,01 |
0,13 |
0,94 |
2,60 |
|
1 T 500 , |
T = 1 |
0,32 |
1,03 |
2,38 |
1 k 10 , |
k = 1 |
0,96 |
1,35 |
2,25 |
Как видно из таблицы 3.1, значения среднеквадратических отклонений,
полученных аналитически по выражению (3.11) и численного моделирования,
различаются не более, чем на 3% для всего диапазона исследования, что соответствует заданной инженерную точности, равной 5%. Полученные результаты

подтверждают работоспособность программного модуля для исследования совместного подобия объектов управления и действующих на них возмущений для имитационного моделирующего комплекса по исследованию подобия систем управления [11].
Таким образом, для оценивания совместного подобия двух комплексов
«объект−воздействия» целесообразно использовать следующее соотношение
k 2 |
|
2 |
|
|
k |
2 |
|
2 |
|
|
|
1 |
|
пр1 |
|
|
2 |
|
пр2 |
|
. 0,05 |
||
1 T |
|
1 T |
|
||||||||
|
|
|
(3.13) |
||||||||
|
1 |
|
1 |
|
|
|
2 |
|
2 |
||
|
|
|
|
|
|
|
|
||||
Поскольку значения времени запаздывания не вошло в условие (3.13), то оно в дальнейшем не учитывалось.
Натурно-модельные исследования
Для проверки соотношения (3.13) в условиях, близких к натурным, были проведены натурно-модельные исследования, для реализации которых в качестве исходных были использованы данные, характеризующие работу двух установок сжигания водоугольного топлива, характеристики которых приведены в [12, 16]. Там были получены следующие значения параметров объектов управления по каналу преобразования «изменения расхода водоугольного топлива – изменения температуры в топке печи» (« Qт → T°C»)
k1=5,4 л/ч; Т1=182 с;
(3.14)
k2=5,9 л/ч; Т2=135 с.
Подстрочные индексы 1 и 2 параметров выражения (3.14) соответствуют принадлежности к первой и второй установкам сжигания водоугольного топлива.
Оценки среднеквадратических отклонений приведенных ко входу возмущений для первого σвх1 и второго σвх2 объектов управления приведены ниже
σвх1=23,5 л/ч; σвх2=19,0 л/ч. |
(3.15) |
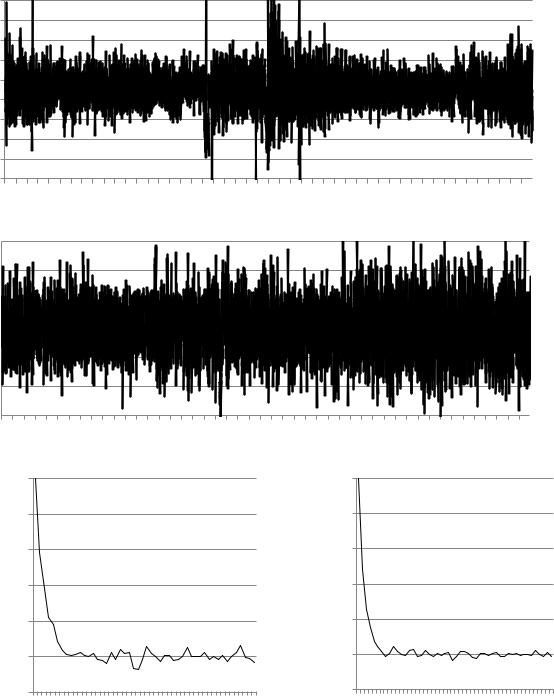
На рисунках 3.2 а, б представлены приведенные ко входу объектов возмущения |
||||||||||
и их нормированные АКФ на рисунках 3.2 в, г соответственно. |
|
|
||||||||
90 |
uпр, л/ч |
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
-10 |
|
|
|
|
|
|
|
|
|
|
-30 |
|
|
|
|
|
|
|
|
|
|
-50 |
|
|
|
|
|
|
|
|
|
|
-70 |
|
|
|
|
|
|
|
|
|
i, с |
-90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
0 |
500 |
1000 |
1500 |
2000 |
2500 |
3000 |
3500 |
4000 |
4500 |
|
|
|
|
|
|
|
|
|
|
|
60 |
|
uпр, л/ч |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-20 |
|
|
|
|
|
|
|
|
|
|
-40 |
|
|
|
|
|
|
|
|
|
|
i, c
|
-60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
0 |
500 |
|
1000 |
|
1500 |
|
2000 |
2500 |
3000 |
|
|
3500 |
4000 |
4500 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
rпр(θ) |
|
|
|
|
|
|
|
|
1 |
rпр(θ) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0,8 |
|
|
|
|
|
|
|
|
|
|
0,8 |
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
-0,2 |
|
|
|
|
|
|
|
|
θ, с |
|
-0,2 |
|
|
|
|
θ, с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) |
1 |
6 |
11 |
16 |
21 |
26 |
31 |
36 |
41 |
46 |
г) |
|
1 |
6 |
11 16 21 26 31 36 41 46 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Рисунок 3.2 – Реализации приведенных к входу возмущений |
||||||||||||||||
|
|
для первого (а) и второго (б) объектов управления и |
|
||||||||||||||
|
|
|
их нормированные АКФ соответственно (в, г) |
|
|||||||||||||
Представленным выше АКФ натурно-модельных рядов данных соответствуют значения следующие параметра α:
α1=0,500; α1=0,524. |
(3.16) |
Для параметров (3.14) – (3.16) условие совместного подобия (3.12) натурно-
модельного объекта и действующих на него приведенных к управляющему входу
возмущений выполняется (значение в процентах модуля разности
среднеквадратических отклонений Δσу=2,4%), что говорит о совместном подобии приведенных возмущений и каналов их преобразования в объекте управления. Первая строка таблицы 3.2 содержит значения параметров натурных объектов (3.14) и
натурно-модельных данных, представленных на рисунке 3.2 и уравнениями (3.15) – (3.16).
В процессе исследования была проведена серия аналогичных натурно-
модельных экспериментов, некоторые результаты которых для примера
представлены в других строках таблицы 3.2.
Таблица 3.2– Значения параметров моделей объекта и воздействий
|
Объект 1 |
|
|
Объект 2 |
|
|
|
||
№ |
α,с-1 |
σпр, |
k,л/ч |
T, с |
α, с-1 |
σпр, |
k, л/ч |
T, с |
Δσy, % |
|
л/ч |
л/ч |
|
||||||
|
|
|
|
|
|
|
|
||
1 |
0,500 |
23,5 |
5,4 |
182,0 |
0,524 |
19,0 |
5,9 |
135,0 |
1,4 |
2 |
0,700 |
23,5 |
5,4 |
182,0 |
0,735 |
19,0 |
5,9 |
135,0 |
2,4 |
3 |
0,500 |
23,5 |
5,4 |
182,0 |
0,500 |
18,6 |
5,9 |
135,0 |
1,1 |
4 |
0,500 |
23,5 |
5,4 |
182,0 |
0,700 |
19,0 |
6,8 |
135,0 |
1,2 |
5 |
0,500 |
23,5 |
5,4 |
182,0 |
0,700 |
19,0 |
5,9 |
101,1 |
2,3 |
Исследование влияния изменений параметров модели объекта управления
и свойств приведенных возмущений на изменения среднеквадратического
отклонения выходного воздействия
Были проведены исследования влияния изменений свойств модели объекта управления (время инерции T, коэффициент передачи k) и статистических характеристик приведенного возмущения (коэффициент спада АКФ ш, дисперсия
σ2пр) на изменения СКО σy, результаты которых представлены на рисунках 3.3 – 3.6 в
виде зависимостей изменения СКО выходного воздействия от изменения указанных параметров.
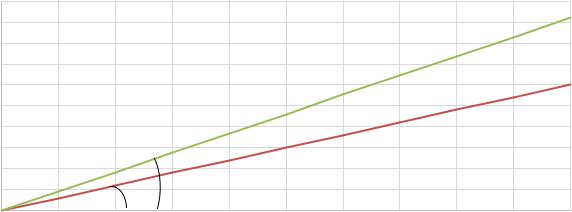
На рисунке 3.3 показано влияние изменения коэффициента передачи на СКО объекта управления. Значение σy прямо пропорционально коэффициенту передачи объекта k. Угол ш зависит от параметров σпр, α, T, таким образом, φ=f(σпр, α, T). Углы
φ1 – φ2 соответствуют следующим условиям моделирования: φ1 : σпр = 2; α=0,1; T = 100; φ2: σпр = 2; α=0,1; T = 200.
10 |
|
|
|
|
|
|
|
|
|
|
|
9 |
σy,усл.ед. |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
φ1 |
φ2 |
|
|
|
|
|
k, усл. ед. |
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Рисунок 3.3 – Влияние коэффициента передачи k на СКО выходного |
|
|||||||||
|
|
|
|
воздействия σy объекта |
|
|
|
|
|||
Влияние изменения величины СКО приведенного возмущения на СКО выходного воздействия объекта представлено на рисунке 3.4. Угол γ зависит от параметров k, α, T, таким образом, γ =f(k, α, T). Углы γ 1 - γ 4 соответствуют следующим условиям моделирования: γ1: k = 1; α=0,1; T = 200; γ2 : k = 1; α=0,05; T = 200; γ3
: k = 1; α=0,05; T = 100; γ4 : k = 2; α=0,05; T = 200. Изменения значение σy прямо пропорционально изменению СКО приведенного возмущения.
30 |
|
|
|
|
|
|
|
|
|
σy,усл.ед. |
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
0 |
|
γ |
γ |
γ |
3 |
γ |
4 |
σпр, усл. ед. |
|
1 |
2 |
|
|
|
|||
0 |
5 |
10 |
15 |
|
|
20 |
25 |
30 |
|
Рисунок 3.4 – Влияние изменения СКО приведенного возмущения |
|||||||
|
|
σпр на СКО выходного воздействия σy объекта |
|
|
||||
0,7 |
|
|
|
|
|
|
|
|
σy,усл.ед. |
Т=100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6 |
|
|
Т=150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
Т=300 |
|
|
|
|
|
|
|
|
|
Т=500 |
|
|
0,4 |
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
α, с-1 |
|
|
|
|
|
|
|
|
|
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
0,1 |
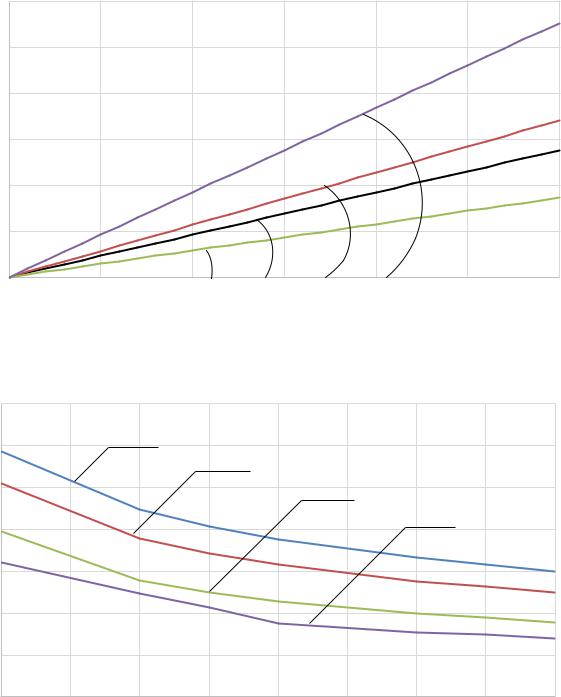
Рисунок 3.5 – Влияние изменения коэффициента спада АКФ приведенного |
||||||||
возмущения α на СКО выходного воздействия σy объекта (k=1, σпр=1) |
|
|||||||
Зависимость изменения σy объекта от изменения параметра спада АКФ α возмущения носит спадающий экспоненциальный характер.
