
4 работа
.pdf
Естественнонаучный
факультет
Кафедра графики и начертательной геометрии
Построение проекций сквозных отверстий в поверхностях вращения
Новокузнецк
2010
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования “Сибирский государственный индустриальный университет”
Кафедра графики и начертательной геометрии
Построение проекций сквозных отверстий в поверхностях вращения
Методические указания к выполнению задания по курсу «Инженерная графика»
Новокузнецк
2010
УДК 514.18 (07) П 637
Рецензент к.т.н., профессор СибГИУ
А.Н. Савельев
П 637 Построение проекций сквозных отверстий в поверхностях вращения (методические указания для студентов первого курса) / Сост.: Л.С. Тропина, Г.И. Живаго, З.В. Шадрина: СибГИУ. – Ново-
кузнецк, 2010. – 19 с., ил.
В методических указаниях указаны цель, назначение и содержание задания, порядок его выполнения. Изложены основы построения проекций сквозных отверстий в поверхностях вращения: цилиндре, конусе, сфере. Приведены примеры выполнения заданий.
Методические указания предназначены для студентов первого курса.
Цель задания − изучение правил построения точек на поверхностях вращения (цилиндрической, конической и сферической) и линий пересечения этих поверхностей плоскостями.
Содержаниеиоформлениезадания
Задание по теме "Построение проекций сквозных отверстий в поверхностях вращения " выполняется по индивидуальным вариантам и включает всебя следующие задачи:
•построение проекций линий сквозного отверстия в цилинд-
ре;
•построение проекций линий сквозного отверстия в конусе;
•построение проекций линий сквозного отверстия в сфере. Каждая задача вычерчивается в трех проекциях на листе фор-
мата A3 в масштабе 1:1. Размеры не проставляются. В нижнем правом углу вычерчивают габаритные размеры основной надписи (форма 1), где указывают Ф.И.О. игруппустудента.
На чертеже сохраняются все построения и обозначения точек и плоскостей. Характерные точки обозначают прописными буквами латинского алфавита, промежуточные точки − цифрами; плоскости − прописными буквами греческого алфавита.
Примеры выполнения задач приведены в приложениях А, Б, В.
Список рекомендуемой литературы
1.Чекмарёв А.А. Начертательная геометрия и черчение: Учебник для студ. высш. учеб. заведений / А.А. Чекмарев – 2-е изд. перераб. и доп. – М.: Высшее образование, 2008. – 471с.: ил.
2.Нартова Л.Г. Начертательная геометрия: Учеб. для вузов/Л.Г. Нартова. В.И. Якунин. – М.: Дрофа, 2008 –304с.: ил.
3.Гордон В.О. Курс начертательной геометрии: Учебное пособие для вузов/ В.О. Гордон, М.А. Семенцов – Огиевский; Под ред. В.О. Гордона. – 29-е изд., стер. – М: Высшая школа, 2009. – 272с.: ил.
3.Лагерь А.И. Инженерная графика: Учебник для втузов / А.И. Лагерь. – 6-е изд., стер. – М.: Высшая школа, 2009 – 336с.: ил.
4.Инженерная графика: учебник для вузов / Н.П. Сорокин и др. – 3-е
изд., стер. – Спб.: «Лань», 2008. – 391с.: ил.
3
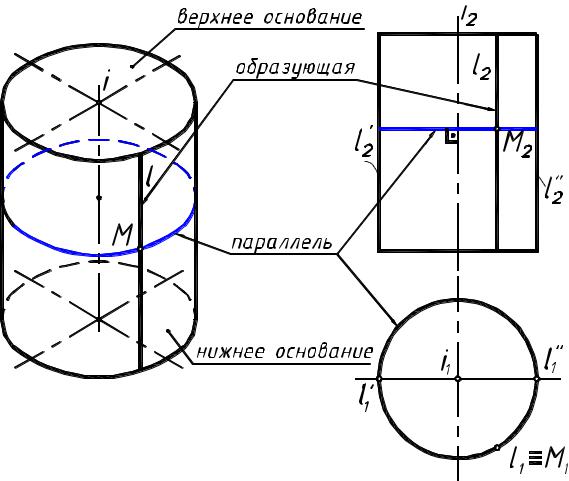
Цилиндрвращения
Цилиндрическая поверхность вращения образуется при враще-
нии прямолинейной образующей l вокруг неподвижной оси i, параллельнойобразующей(рисунок1).
Каждая точка М образующей l при вращении описывает окружность с центром на оси i. Эти окружности называются параллелями. При изображении цилиндра вращения на комплексном чертеже обычно его располагают так, чтобы ось i была перпендикулярна к плоскости проекций. На рисунке 1 ось i перпендикулярна горизонтальной плоскости проекций П1, в этом случае все параллели проецируются на горизонтальную плоскость проекций П1 без искажения и определяют горизонтальный очерк цилиндра. Образующие, ограничивающие цилиндр на фронтальной плоскости проекций П2 называются очерковыми образующими (l' и l'').
Рисунок 1 4
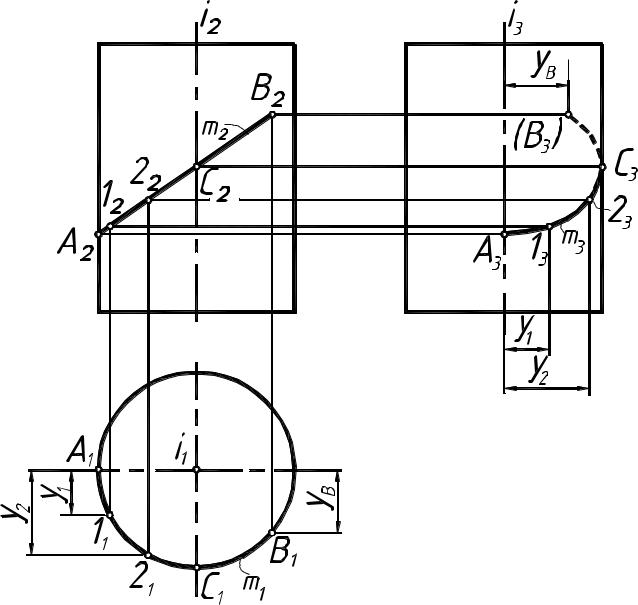
Видимостьэлементовцилиндра
Нагоризонтальнойплоскости П1 видимойбудетплоскость верхнего основания цилиндра. На фронтальной плоскости видима передняя часть цилиндрической поверхности. Проекции очерковых образующих l' и l'' (рисунок 1) отделяют видимую часть цилиндра от невидимой. На профильной плоскости видима левая часть цилиндра (рисунок 2).
Рисунок 2
5
Построениелинии, лежащейнаповерхностицилиндра
Задана фронтальная проекция линии m(m2), лежащей на цилиндрической поверхности (рисунок2).
Отмечаем характерные точки этой линии A, B, C: А, В − экстремальные (низшая и высшая) точки; А, С − точки, принадлежащие очерковым образующим. Точки 1 и 2 − промежуточные (случайные) точки. Горизонтальные проекции всех точек совпадают с окружностью, которая является горизонтальной проекцией цилиндрической поверхности. Координатным способом определяем профильные проекции точек и соединяем их плавной кривой. Часть профильной проекции кривой m(m3) − B3С3 не видима, так как она лежит за очерковыми образующими на поверхности цилиндра.
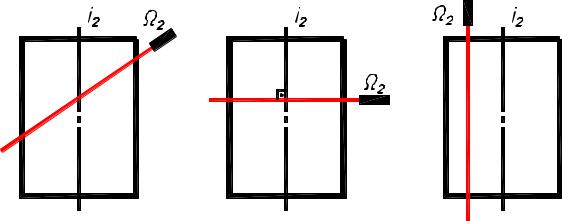
Линии пересечения цилиндрической поверхности вращения плоскостями
Цилиндр вращения пересекается плоскостью в общем случае по эллипсу (рисунок 3, а). Если секущая плоскость перпендикулярна или параллельна оси вращения цилиндра, то в сечении получается соответ-
ственно окружность (рисунок 3, б) или две образующие (рису-
нок3, в).
а |
б |
в |
Рисунок3
6
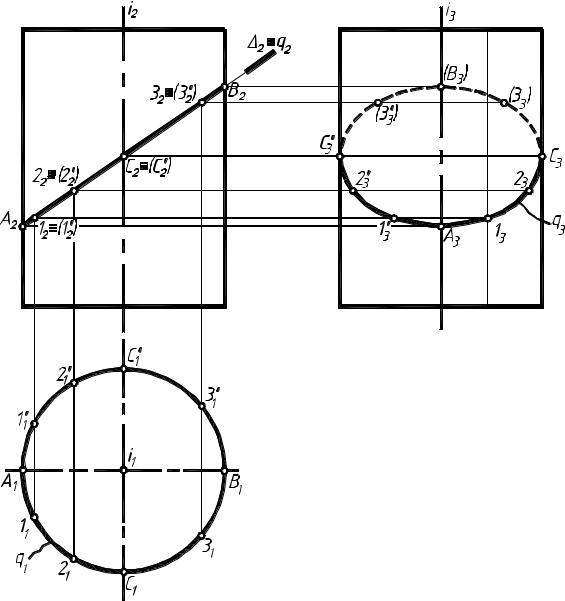
Построениелиниипересеченияцилиндра фронтально-проецирующей плоскостью
При пересечении цилиндра плоскостью ∆ (рисунок 4) получается линия q − эллипс, так как секущая плоскость пересекает все образующие цилиндра. БольшойосьюэллипсаявляетсяотрезокАВ(А2В2), амалой − отрезок СС' (С1С'1) , т.е. диаметр цилиндра. Точки А, В, С, С' являются характерными, а лежащие между ними 1, 1', 2, 2', 3, 3' – промежуточными. Построения линии пересечения необходимо начинать с характерных точек.
Рисунок4 7
Фронтальная проекция линии пересечения q (q2) − отрезок │А2В2│, а горизонтальная проекция линии пересечения q (q1) проецируется на плоскость П1 в окружность. Профильная проекция линии пересечения q (q3) − эллипс, большаяось(С3С'3) котороговданномслучае равна диаметру цилиндра, а малая (А3В3) − профильная проекция отрезка АВ.
Для построения профильных проекций точек проводят горизонтальные линии связи до пересечения с профильными проекциями соответствующих образующих. Профильные проекции точек В(В3), 3(33), 3'(3'3) на плоскости П3 − не видимы.
Полученные проекции точек соединяют плавной линией при помощи лекала с учетом видимости.
Конусвращения(прямой круговой конус)
Коническая поверхность вращения образуется вращением прямолинейной образующей l вокруг пересекающейся с ней осью i (рисунок 5). Точка пересечения образующей l и оси i называется вершиной конуса S.
На конусе имеются следующие группы линий:
образующие − линии, которые лежат на поверхности конуса в плоскостях, проходящих через вершину S;
параллели − окружности, лежащие на поверхности конуса в плоскостях, перпендикулярных оси вращения.
Видимость элементов конуса
Видимость элементов конуса рассматривается на примере конуса с горизонтально-проецирующей осью (рисунок 5).
На горизонтальной плоскости проекций П1 видимой будет вся боковая поверхность конуса. На фронтальной плоскости проекций П2 видимость определяется при помощи крайних образующих AS и BS, так как эти образующие являются очерковыми образующими по отношению к плоскости проекций П2. На фронтальной плоскости проекций П2 видима передняя часть конической поверхности. На профильной плоскости проекций П3 видима левая часть конуса, ограниченная проекциями образующих CS и DS. Эти образующие являются очерковыми образующими по отношению к плоскости проекций П3.
8
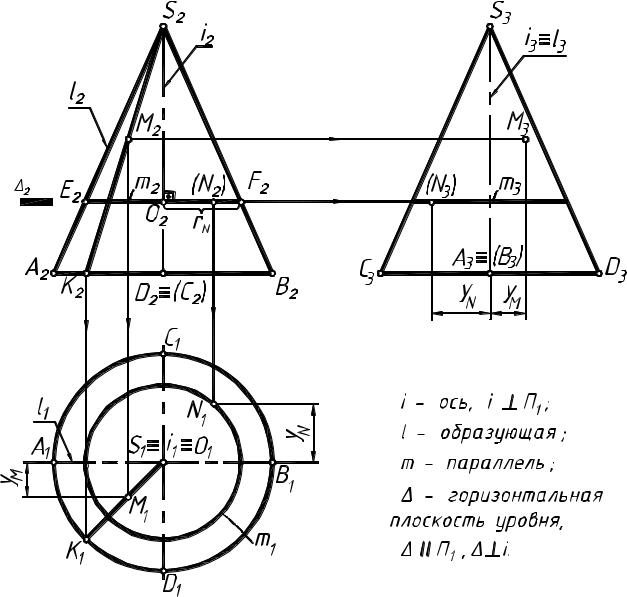
Рисунок 5
Построение проекций точек, лежащих на поверхности конуса
Точка принадлежит поверхности конуса, если она лежит на ка- кой-либо линии, принадлежащей этой поверхности. В качестве вспомогательных линий используют образующие или параллели.
На рисунке 5 показано построение двух произвольных точек М (М1, М2, М3) и N (N1, N2, N3), принадлежащих поверхности конуса.
9
