
- •1)Применение 1-го начала термодинамики к адиабатному процессу.
- •2)Электроемкость.
- •1)Работа и кинетическая энергия
- •2)Напряженность электростатического поля.
- •1)Ускорение произвольного движения
- •2)Цикл Карно
- •2)Типы диэлектриков. Их поляризация.
- •1)Цикл Карно(см.Билет 4 вопрос 2)
- •1)Теплоёмкости. Внутренняя энергия газа
- •2)Основной закон динамики вращения
- •1)Работа газа при расширении.
- •2)Закон сохранения момента импульса
- •1)Закон сохранения механической энергии
- •2)Второе начало термодинамики
- •1)Применение 1-го начала к изотермическому процессу
- •2)Энергия заряженного проводника
- •1)Скорость произвольного движения
- •2)Напряженность электрического поля между двумя бесконечными равномерно-заряженными плоскостями
- •1)Основные параметры динамики поступательного движения
- •2)Применение уравнения состояния идеального газа для изопроцессов
- •1)Закон сохранения момента импульса(см билет 8,вопрос 2)
- •2)Напряженность электростатического поля от бесконечной равномерно-заряженной плоскости.
- •1)Применение первого начала к изобарному процессу
- •2)Вектор электрического смещения . Теорема Остроградского-Гаусса.
2)Закон сохранения момента импульса
Моментом
импульса (количества движения) материальной
точки А относительно неподвижной точки
О называется физическая величина,
определяемая векторным произведением:
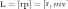
где r - радиус-вектор, проведенный из точки О в точку A, p=mv – импульс материальной точки
При
вращении абсолютно твердого тела вокруг
неподвижной оси z каждая точка тела
движется по окружности постоянного
радиуса riсо
скоростью vi .
Скорость vi и
импульс mivi перпендикулярны
этому радиусу, т. е. радиус является
плечом вектора mivi .
Значит, мы можем записать, что момент
импульса отдельной частицы равен
 (1)
и
направлен по оси в сторону, определяемую
правилом правого винта.
Монет
импульса твердого тела относительно
оси есть сумма моментов импульса
отдельных частиц:
(1)
и
направлен по оси в сторону, определяемую
правилом правого винта.
Монет
импульса твердого тела относительно
оси есть сумма моментов импульса
отдельных частиц: Используя
формулу vi =
ωri,
получим
Используя
формулу vi =
ωri,
получим
 т.
е.
т.
е. 2)
Таким
образом, момент импульса твердого тела
относительно оси равен моменту инерции
тела относительно той же оси, умноженному
на угловую скорость. Продифференцируем
уравнение (2) по времени:
2)
Таким
образом, момент импульса твердого тела
относительно оси равен моменту инерции
тела относительно той же оси, умноженному
на угловую скорость. Продифференцируем
уравнение (2) по времени: т.
е.
т.
е. Эта
формула - еще одна формауравнения
динамики вращательного движения твердого
тела относительно
неподвижной оси: производная момента
импульса твердого тела относительно
оси равна моменту сил относительно той
же оси.
Можно показать, что имеет
место векторное равенство
Эта
формула - еще одна формауравнения
динамики вращательного движения твердого
тела относительно
неподвижной оси: производная момента
импульса твердого тела относительно
оси равна моменту сил относительно той
же оси.
Можно показать, что имеет
место векторное равенство
 (3)
В
замкнутой системе момент внешних
сил
(3)
В
замкнутой системе момент внешних
сил и
и откуда
откуда (4)
Выражение
(4) представляет собойзакон
сохранения момента импульса:
момент импульса замкнутой системы
сохраняется, т. е. не изменяется с течением
времени.
(4)
Выражение
(4) представляет собойзакон
сохранения момента импульса:
момент импульса замкнутой системы
сохраняется, т. е. не изменяется с течением
времени.
Здесь мы продемонстрируем закон сохранения момента импульса с помощью скамьи Жуковского. Человек, сидящий на скамье, вращающаяся вокруг вертикальной оси, и держащий в вытянутых руках гантели (рис. 2), вращается внешним механизмом с угловой скоростью ω1. Если человек прижмет гантели к телу, то момент инерции системы уменьшится. Но момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость вращения ω2 увеличивается. Аналогичным образом, гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, с целью уменьшить свой момент инерции и тем самым увеличить угловую скорость вращения.

Билет № 9
1)Закон сохранения механической энергии
Рассмотрим процесс изменения состояния тела, поднятого на высоту h. При этом его потенциальная энергия

Тело
начало свободно падать 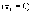 .
Из кинематики известно, что момент
достижения поверхности земли оно будет
иметь скорость
.
Из кинематики известно, что момент
достижения поверхности земли оно будет
иметь скорость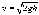 икинетическую
энергию:
икинетическую
энергию:

Кинетическая энергия тела, упавшего с высоты h, оказалась равной его потенциальной энергии, которую оно имело до начала падения. Следовательно:

На
поверхности Земли h=0 и потенциальная
энергия 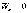 ,
а
,
а -максимальна.
В начале падения
-максимальна.
В начале падения ,
а
,
а т.е.
потенциальная энергия переходит
(превращается) в кинетическую. Таким
образом, при падении тела в системе
тело-Земля кинетическая энергия
возрастает и, следовательно, ее
изменение
т.е.
потенциальная энергия переходит
(превращается) в кинетическую. Таким
образом, при падении тела в системе
тело-Земля кинетическая энергия
возрастает и, следовательно, ее
изменение равное
работе
равное
работе ,
имеет положительный знак, т.е.
,
имеет положительный знак, т.е.
|
|
(4.12) |
Потенциальная энергия - уменьшается, и, следовательно, ее изменение имеет знак минус. Поэтому можем записать:
|
|
(4.13) |
Сложив (4.12) и (4.13), получим

или 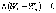
Сумма 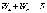 представляет
собой полную энергию, и, следовательно,
представляет
собой полную энергию, и, следовательно,
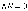 ,
а
,
а
|
|
(4.14) |
Таким образом, энергия замкнутой консервативной системы остается постоянной при всех, происходящих в ней процессах и превращениях. Энергия может переходить из одних видов в другие (механические, тепловые, и т.д.), но общее ее количество остается постоянным. Данное положение называют законом сохранения и превращения энергии.



