
- •В.Ю. Островлянчик
- •Краткие сведения по истории развития теории автоматического управления (тау)
- •Глава 1. Основные принципы построения систем автоматического управления
- •Основные понятия и определения теории автоматического управления
- •Графическое изображение сау
- •Принципы автоматического управления
- •Принцип разомкнутого управления.
- •Принцип управления по отклонению (Принцип Ползунова-Уатта).
- •Принцип управления по возмущению.
- •Принцип комбинированного управления.
- •Принцип адаптации.
- •Принципы классификации сау
- •Глава 2. Методы математического описания и характеристики линейных сау
- •2.1 Математическое описание линейных сау
- •2.2 Уравнения звеньев системы. Линеаризация
- •2.3 Основные свойства преобразования Лапласа. Понятие о передаточной функции
- •2.4 Примеры составления передаточных функций и структурных схем сау
- •Типовые воздействия и временные характеристики систем (элементов) автоматического управления
- •Единичная ступенчатая функция 1(t).
- •Единичная импульсная функция δ(t).
- •Гармоническое воздействие.
- •Временные характеристики сау.
- •Логарифмические частотные характеристики
- •Глава 3. Характеристики и модели типовых динамических систем управления
- •Общая характеристика линейных динамических звеньев
- •Пропорциональное безинерционное (масштабное) звено
- •Интегрирующее звено
- •Дифференцирующее звено
- •Инерционное (апериодическое) звено
- •Реальное дифференцирующее звено (инерционно-дифференцирующее звено)
- •3.7 Форсирующее звено
- •Общее понятие о колебательном звене
- •Неминимально-фазовые звенья
- •Звенья с запаздыванием
- •Глава 4. Характеристики разомкнутых и замкнутых сау
- •Соединение линейных звеньев
- •Последовательное соединение звеньев.
- •Параллельное соединение звеньев.
- •Передаточные функции замкнутых систем. Встречно-параллельное включение звеньев.
- •Правила преобразования структурных схем
- •Перенос точки приложения возмущающего воздействия.
- •Перенос точки съема внутренних обратных связей.
- •Перемещение суммирующего узла через узел разветвления.
- •Передаточные функции разомкнутых и замкнутых сау
- •Построение частотных характеристик системы по частотным характеристикам звеньев
- •Построение логарифмических частотных характеристик разомкнутой одноконтурной системы
- •Глава 5. Статические режимы сау
- •Понятие статики в теории автоматического управления
- •2 Астатическое регулирование
- •Глава 6. Устойчивость систем автоматического управления
- •1 Понятие об устойчивости
- •Критерий устойчивости Рауса - Гурвица
- •Критерий устойчивости Михайлова
- •Критерий устойчивости Найквиста
- •Влияние на устойчивость параметров и структуры сау
- •Влияние на устойчивость последовательного включения апериодического звена.
- •Включение последовательно со статической сар двухкратноинтегрирующих звеньев.
- •Запас устойчивости сау
- •Суждение об устойчивости по амплитудным и фазовым характеристикам
- •Суждение об устойчивости по логарифмическим амплитудным и фазовым характеристикам
- •Влияние параметров системы на ее устойчивость. Исследование сар построением областей устойчивости (d-разбиения)
- •Построение области устойчивости в плоскости двух параметров
- •Глава 7. Оценка качества управления
- •Понятие о качестве переходных процессов
- •Частотные критерии качества переходного процесса
- •Оценка качества переходного процесса по высокочастотной характеристике замкнутой системы
- •Корневые критерии качества переходного процесса
- •Интегральные оценки качества
- •Глава 8. Коррекция динамических свойств сау
- •Понятие о коррекции динамических свойств сау
- •Последовательные корректирующие звенья в контуре сау
- •Коррекция с помощью интегрирующих звеньев.
- •Коррекция с помощью интегро-дифференцирующих устройств.
- •Параллельные корректирующие звенья. Жесткие корректирующие обратные связи
- •Гибкие обратные связи
- •Идеальная гибкая обратная связь.
- •Гибкая обратная связь по ускорению.
- •Гибкая инерционная обратная связь.
- •Охват обратной связью пропорционального звена с большим kо
- •Глава 9. Синтез корректирующих устройств
- •9.1 Синтез последовательных корректирующих устройств по логарифмическим характеристикам
- •9.2 Синтез параллельной коррекции по обратным афчх
- •9.3 Синтез параллельных корректирующих устройств по лах разомкнутой системы
- •9.4 Понятие о параметрическом синтезе систем автоматического управления
- •Общие принципы синтеза алгоритмической структуры системы управления
- •Осуществление инвариантности в стабилизирующих и следящих системах
- •Глава 10. Построение кривой переходного процесса
- •10.1 Общие соображения
- •10.2 Аналитические методы
- •10.3 Графические методы
- •10.4. Метод математического моделирования на аналоговых вычислительных машинах
- •Глава 11. Математическое моделирование систем автоматического управления на эвм
- •Основы построения цифровых моделей
- •Обзор методов моделирования
- •Методы цифрового моделирования систем автоматического управления электроприводами постоянного тока
- •Список рекомендуемой литературы Основная
- •Дополнительная
- •Содержание
Параллельные корректирующие звенья. Жесткие корректирующие обратные связи

Рисунок 8.10 Эквивалентная алгоритмическая схема параллельной коррекции
Корректирующие обратные связи делятся на отрицательные и положительные, на жесткие и гибкие.
Жесткая обратная связь осуществляется усилительным звеном, т.е. Wос(0)0 при p=0.
Гибкая обратная связь осуществляется дифференцирующим звеном, т.е. Wос(0)=0.
В статике сигнал гибкой обратной связи отсутствует. Она действует только в динамике.
Идеальная жесткая обратная связь Wос=kос.
Рассмотрим охват такой обратной связью
простого статического звена с![]() :
:
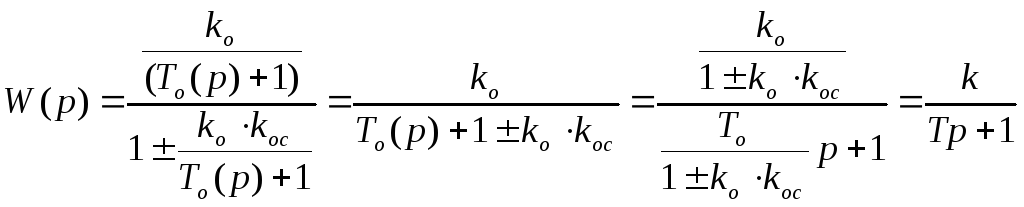 (8.9)
(8.9)
![]() (8.10)
(8.10)
Охват статического звена жесткой обратной связью изменяет kиТ в(1kokoc) раз, т.е. они уменьшаются при отрицательной обратной связи и увеличиваются при положительной обратной связи.
Покажем, как изменяется переходная функция h(t)при отрицательной обратной связи (рисунок 8.11).
Для кривой
![]() - величина на входе звенаWо
Xвх(t)имеет всплеск. За
счет этого всплеска и происходит
форсировка на входе, что дает ускорение
переходного процесса.
- величина на входе звенаWо
Xвх(t)имеет всплеск. За
счет этого всплеска и происходит
форсировка на входе, что дает ускорение
переходного процесса.
Для коррекции переходных процессов, т.е. для уменьшения инерционности, в основном применяется отрицательная обратная связь. Кроме этого отрицательная обратная связь:
Уменьшает нелинейность статической характеристики звена.
Уменьшает нестабильность параметров звена во времени.
Уменьшает величину шумов на выходе.
Повышает устойчивость.

Рисунок 8.11 Переходная функция в случае отрицательной обратной связи
Также действует жесткая обратная связь и на звено более высокого порядка.
Интересен случай охвата жесткой обратной
связью интегрирующего звена с
![]() .
.
 , (8.11)
, (8.11)
т.е. получили статическое звено, где
![]() ;
;![]() .
.
При охвате интегрирующего звена жесткой обратной связью оно превращается в апериодическое звено. Практически важна здесь отрицательная обратная связь. Эта связь широко применяется для снижения порядка статизма и для улучшения устойчивости и качества переходного процесса.
Гибкие обратные связи
Идеальная гибкая обратная связь.
В качестве корректирующего звена выберем идеальное дифференцирующее звено.
![]() .
.
Пусть охваченное звено имеет:
![]() ,
,
тогда:
 .
(8.12)
.
(8.12)
Гибкая обратная связь не влияет на коэффициент передачи охватываемого звена и изменяет коэффициент при рв знаменателе передаточной функцииW.
Рассмотрим пример 1:
![]()
![]()
где
![]() .
.
Постоянная времени Т изменилась на kokoc.
При отрицательной обратной связи Т увеличивается.
При положительной обратной связи Т уменьшается.
Таким образом, гибкая обратная связь изменяет быстродействие без изменения коэффициента передачи звена.
В звене второго порядка гибкая обратная связь сильно уменьшает коэффициент передачи.
Положительная гибкая обратная связь форсирует переходный процесс, как при возрастании, так и при снижении выходного сигнала САР.
Рассмотрим пример 2:
Охват дифференцирующей связью с
![]() интегрирующего звена с
интегрирующего звена с![]() .
.
 , (8.13)
, (8.13)
где
![]() .
.
Гибкая обратная связь изменяет коэффициент передачи, не меняя типа звена.
Гибкая обратная связь по ускорению.
![]() (8.14)
(8.14)
 . (8.15)
. (8.15)
Такая обратная связь изменяет коэффициент при p2. Эта связь применяется для систем 2-го и более высокого порядка.
Гибкая инерционная обратная связь.
Реальное дифференцирующее звено:
![]() .
(8.16)
.
(8.16)
Если такой обратной связью охватить интегрирующее звено, то процесс действия обратной связи можно объяснить так.
Начало переходного процесса. Скорость
изменения y(t)велика и в Wосможно пренебречь,![]() .
.
В начале переходного процесса гибкая инерционная обратная связь ведет себя как жесткая обратная связь, а охваченное ей интегрирующее звено превращается в апериодическое.
При этом можно повысить быстродействие в начале переходного процесса увеличением коэффициента передачи.
Вторая половина переходного процесса. Постепенно по мере замедления переходного процесса Хосспадает до нуля (действует числительWос) и интегрирующее звено начинает вести себя как звено без обратной связи. В статике обеспечивается астатизм системы (ошибка = 0).
