
- •Содержание
- •Логические основы компьютера
- •Цель работы
- •Логические основы компьютера Понятие логического высказывания
- •Основные логические операции и таблицы истинности
- •Логическое отрицание
- •Логическое умножение
- •Логическое сложение
- •Импликация
- •Эквивалентность
- •Строгая дизъюнкция
- •Логические формулы и функции Логическая формула
- •Определение логической (булевой) функции
- •Законы логики
- •Упрощение логических выражений
- •Построение логических функций на основе математических выражений
- •Методы решения логических задач
- •Решение логических задач средствами алгебры логики
- •Решение логических задач табличным способом
- •Решение логических задач с помощью рассуждений
- •Логические элементы компьютера Понятие вентиля
- •Построение логических схем
- •Вопросы для самоконтроля
- •Задачи и упражнения
- •Рекомендуемая литература
- •Логические основы компьютера
- •654007, Г. Новокузнецк, ул. Кирова,42
Упрощение логических выражений
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Под упрощением формулы понимают равносильное преобразование, приводящее к формуле, которая либо не содержит операций импликации, эквиваленции и строгой дизъюнкции, либо содержит по сравнению с исходной меньшее число операций конъюнкции, дизъюнкции и инверсий, либо содержит меньшее число переменных.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул.
В этом примере применены законы противоречия (11) и исключения констант (7).
В этом примере применён закон противоречия (11) и определение операции «Логического сложения».
В примере 3 применены законы противоречия (11) и исключения констант (7).
В примере (4) применён закон противоречия (11) и определение операции «Логического умножения».
Законы алгебры логики в этом примере применяются в следующей последовательности: правило де Моргана (14), сочетательный закон (6), закон противоречия (11) и правило операций с константами (7).
Законы алгебры логики в этом примере применяется в таком порядке: правило де Моргана (14), выносится за скобки общий множитель (закон дистрибутивности (8)), закон противоречия (11).
В этом примере к отрицаниям неэлементарных формул применяется правило де Моргана ((14) и (15)); сочетательный закон (6), используются законы двойного отрицания (13) и определение операции «Логического сложения».
Часто для упрощения логических выражений применяют следующие тождества:
![]()
Использование этих формул означает, что любое выражение можно умножить на единицу или к любому выражению добавить нуль. Пример:
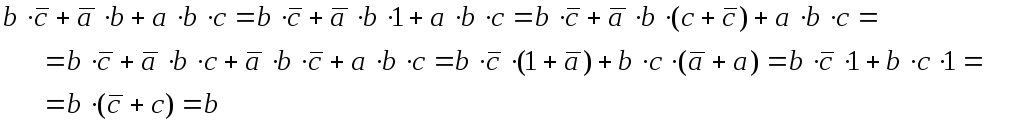
Из этих примеров видно, что при упрощении логических формул не всегда очевидно, какой из законов алгебры логики следует применить на том или ином шаге. Навыки приходят с опытом.
Построение логических функций на основе математических выражений
Логические функции часто формируют на основе математических выражений. Математическое выражение, как известно, содержит переменные, константы и функции, соединённые знаками математических операций. Но для создания логической функции обязательно использование операций отношения: <, >, ≤, ≥, =, ≠. Результат любой из этих операций является «истина» или «ложь», которые мы условились обозначать 1 или 0. Таким образом, каждая операция отношения создаёт одно простое высказывание.
Например, выражение X >Y принимает значение 0 или 1 в зависимости от конкретных значений X и Y. Таким образом, можно сформировать логическую функцию f от действительных переменных X и Y, которая будет истинной, если выполняется указанное выше условие. Записывается это так:
f(X, Y) = X > Y.
Другой пример. Сформировать логическую функцию, которая будет истинной, если переменные x и y кратны трём; x, y – переменные целого типа.
Решение. Заметим, что целое число а будет кратно целому числу b, если остаток от целочисленного деления а на b будет равен нулю:
a mod b = 0.
Здесь запись mod означает операцию вычисления остатка при целочисленном делении а на b.
В условии задачи легко выделить два простых высказывания: x кратно трём и y кратно трём. Между этими высказываниями стоит союз «и». Следовательно, это сложное высказывание содержит операцию логического умножения, а математически это высказывание можно записать так:
f(x, y) = (x mod 3 = 0)∙(y mod 3 = 0).
Рассмотрим ещё один пример. Сформировать логическую функцию, которая будет истинной, если сумма a и b – положительна, а величины a или b - отрицательны. a и b – переменные действительного типа.
Решение. В этом примере также можно выделить несколько простых высказываний:
сумма a и b – положительна;
величина a - отрицательна;
величина b - отрицательна.
Первое высказывание с двумя другими связывается союзом «а», что означает между ними операцию логического умножения. Далее, второе и третье простые высказывания соединены союзом «или», что означает между ними операцию логического сложения. Таким образом, мы получаем следующую функцию:
f(a, b) = ((a + b) > 0) ∙ ((a < 0) + (b < 0)).
Скобки в этом выражении изменяют порядок выполнения операций. Это необходимо, так как операции отношения имеют самый низкий приоритет.
Ещё один класс операций отношения связан с координатной плоскостью. Приведём простой пример: сформировать логическую функцию, которая будет истинной, если точка принадлежит заштрихованной области (смотри рис. 1).
Решение. Согласно рисунку, точка должна быть внутри окружности радиуса 1 с одной стороны, а с другой – быть в верхней полуплоскости. Уравнение окружности радиуса 1 имеет вид:
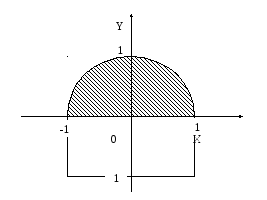
Рис. 1
X2 + Y2 = 1,
где X и Y – координаты точки, принадлежащей окружности. Точка будет внутри этой окружности, если её координаты удовлетворяют условию:
X2 + Y2 ≤ 1.
Чтобы точка была в верхней полуплоскости необходимо выполнение условия Y ≥ 0. Оба эти условия должны выполняться одновременно, что возможно только для операции логического умножения. Таким образом, искомая функция имеет вид:
f(X, Y) = (X2 + Y2 ≤ 1) ∙ (Y ≥ 0).
