Импликация
Импликация или логическое следование соответствует обороту «если..., то...», обозначается A→ B. Таблица истинности импликации имеет вид:
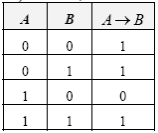
Высказывание A→ B ложно в том и только в том случае, когда условие (первое высказывание A) истинно, а следствие (второе высказывание B) ложно.
Пример:
A = «Завтра будет хорошая погода»
В = «Я пойду гулять»
A→ B = «Если завтра будет хорошая погода, я пойду гулять»
Другой пример сложного высказывания: «Если поезд прибывает на данный путь, то подается сигнал, что путь закрыт».
A= « Поезд прибывает на данный путь»
В= «Подается сигнал, что путь закрыт»
Рассматриваемое сложное высказывание истинно, если:
1) поезд прибывает, сигнал «закрыт» (1, 1, 1);
2) поезд не прибывает, сигнал «свободен» (0, 0, 1);
3) поезд не пребывает, сигнал «закрыт» (0, 0, 1) - если поезд не пребывает, безопасен любой сигнал.
Высказывание ложно (безопасность не обеспечивается) только в том случае, если поезд прибывает, а сигнал «свободен» (1, 0, 0).
Операция импликации в русском языке является самой «загадочной». Ей соответствую также следующие речевые обороты: «из А следует В»; «В только в случае А»; «А влечет В»; «А достаточно для В»; «В необходимо для А».
В обычной речи связка "если ..., то…" описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается. Рассматривается только их истинность или ложность. Поэтому не надо смущаться "бессмысленностью" импликаций, образованных высказываниями, совершенно не связанными по содержанию. Например, такими: "если президент США — демократ, то в Африке водятся жирафы", "если арбуз — ягода, то в бензоколонке есть бензин".
Эквивалентность
Эквивалентность (равноценность или равнозначность) соответствует оборотам речи «тогда и только тогда», «в том и только в том случае», «... равносильно ...» и обозначается A↔B , или A≡B.
Таблица истинности эквивалентности имеет вид:
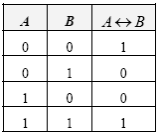
Выражение A↔B истинно в том и только в том случае, когда оба исходных высказывания одновременно истинны или одновременно ложны.
Пример эквивалентности: «Петя выучит уроки тогда и только тогда, когда Пете поставят хорошую отметку».
В русском языке операции эквивалентности также соответствует речевой оборот «A необходимо и достаточно B».
Строгая дизъюнкция
Строгая
дизъюнкция или
«исключающее или», соответствует
оборотам речи «или...,
или...»
или «либо...,
либо...»,
и обозначается A
B
.
Таблица истинности эквивалентности имеет вид:
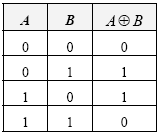
Выражение
A
B
истинно
в том и только в том случае, когда исходные
высказывания A
и
B
не
равны между собой.
Это определение можно обобщить для любого количества логических переменных, объединенных строгой дизъюнкцией. Например,
A
B
C = 1,
(3)
только если одно из трёх высказываний A, B, C истинно.
Логические формулы и функции Логическая формула
С помощью логических переменных и символов логических операций любое сложное (составное) высказывание можно записать в виде логической формулы. Её определение:
Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") — формулы.
Если А и В — формулы, то
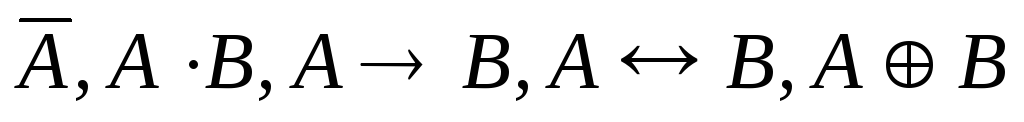- тоже формулы.Никаких других формул в алгебре высказываний нет.
Значение логической формулы определяется заданными значениями входящих в формулу переменных. Тем самым каждая формула может рассматриваться как способ задания функции в алгебре высказываний.