1.6.2. Построение графиков функций одной переменной

Часто возникает необходимость в построении графиков некоторых функциональных зависимостей y=f(x). Пока остановимся на графиках функций одной переменной, напримерx. Пустьexpr- некоторое выражение, зависящее отx, напримерx²— квадратичная зависимость, sin(x) — синусоидальная зависимость и т. д.

Пример 1.6.Построить график функцииf(x):=sin(x)³, задав изменениеxот -10 до 10 с шагом 0,1. Для этого:

1. введите функцию пользователя, набрав выражение f(x):=sin(x)^3;

2. введите ранжированную переменную x:=-10, -9.9 .. 10;

3. в панели математических знаков щелкните на кнопке с изображением графика — на экране появится палитра графиков;

4. в палитре графиков щелкните на кнопке с изображением двумерного графика — на экране появится шаблон графика с уже введенной по оси Y функцией;

5. введите в место ввода у оси x имя независимого аргумента — x;

6. щелкните вне пределов графика левой кнопкой мыши — график будет построен;

7. введите в область графика курсор мыши и дважды щелкните левой клавишей мыши. В появившейся панели форматирования графика задайте его параметры (тип осей, цвет линии и ее тип) так, чтобы получить график, представленный на рис. 1.8.

Рис. 1.8. График функции одной переменной и

панель его форматирования

Заметьте, что вы можете «ухватиться» курсором мыши за рамку выделенного графика и перенести его в любое удобное место в окне документа. Вы можете также растягивать график по вертикали, горизонтали и диагонали, «цепляясь» курсором мыши за соответствующие темные прямоугольники на линиях выделения графика.

Обратите внимание: когда график находится в рамке, на нем в характерных черных уголках появляются числа, идентифицирующие масштаб графика по оси Y и по оси X. По умолчанию по оси X график строится на отрезке изменения аргумента xот –10 до +10. Масштаб по оси Y Mathcad устанавливает по умолчанию автоматически. Изменив эти числа, можно задать свой масштаб графика.

Пример 1.7.Построить на одном рисунке графики двух функций:sin(x)², sin(x)/x иcos(x). Для этого их надо просто перечислить после первой функции в месте ввода возле оси Y, отделяя выражения для функций запятыми. Полученный график представлен на рис. 1.9.

Рис. 1.9.Двумерный график с тремя кривыми

Обратите внимание на то, что Mathcad автоматически отображает каждую кривую своим стилем и своим цветом. И делает это весьма недурно — редко кто из пользователей вмешивается в решение системы. Но форматированием графиков их вид можно менять, например, для изменения стиля и цвета линий, нанесения на график масштабной сетки, изменения фона, нанесения у координатных осей надписей и так далее.

1.6.3. Построение графиков поверхностей

Построение графиков поверхностей (их называют также трехмерными или 3D-графиками) – сложная задача. Связано это с тем, что такие графики даже в простейшем случае требуют создания матрицы точек (аппликат) зависимости z(x,y), то есть функции двух переменных. Создание такой матрицы – нетривиальная задача, что приводило не только к усложнению построений, но и к потере их наглядности.

Однако в новейших версиях Mathcad 2000/2001/2001i/11 эта трудность блестяще преодолена. Теперь трехмерный график построить даже проще, чем двумерный (см. пример ниже).

Пример 1.8. Построить график параболической поверхности (x² + y²). Для этого надо выполнить представленные ниже действия.

1. Определите функцию z(x,y) двух переменных x и y. В качестве примера рассмотрим график функции суммы квадратов(x² + y²). Тогда определение функции будет выглядеть следующим образом:

z(x,y) := x² + y².

2. Используя палитру графики, введите шаблон трехмерного графика.

3. На единственное место ввода под шаблоном введите имя функции — z.

4. Выведите указатель мыши за пределы графика и щелкните левой кнопкой мыши — будет построен график в виде «проволочного каркаса».

5. Растяните (или сожмите) график и поместите его в нужное место экрана (рис. 1.10).

6. Поместив в окно графика курсор мыши и нажав и удерживая левую клавишу мыши, попробуйте вращать график перемещением мыши. Тем самым вы можете менять углы обзора графика и даже заставить график вращаться в заданном направлении автоматически.

Р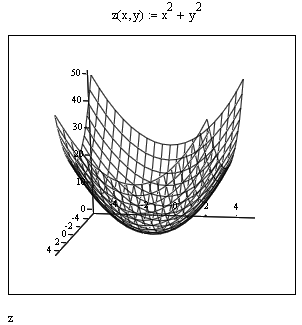ис. 1.10. График поверхности в виде «проволочного каркаса»

Обратите внимание на то, что в этом примере мы впервые задали функцию пользователя как функцию двух переменных x и y. Наша функция пользователя имеет простое имя z и список параметров (x, y), т. е. переменных x и y, от которых зависят значения z. С помощью функций пользователя мы можем пополнять набор функций, встроенных в систему.

График в виде «проволочного каркаса» не слишком эстетичен, хотя иногда и полезен, поскольку сквозь каркас видны обычно невидимые детали. Для изменения вида графиков трехмерных поверхностей используется их форматирование. Окно форматирования имеет множество возможностей, включая изменение типа графиков.

Пример 1.9.Отформатировать представленный в предыдущем примере график с тем, что бы он представлял поверхность в виде контурных линий (рис. 1.11). Такие линии образуются при пересечении поверхности рядом параллельных плоскостей, расположенных на одинаковом расстоянии друг от друга.

Рис. 1.11. Контурный график поверхности с функциональной окраской и оцифровкой контурных линий

Новые версии Mathcad дают возможность построения на одном графике ряда поверхностей. Это делается предельно просто: определите ряд функций двух переменных, описывающих поверхности, и введите через запятую имена этих функций в месте ввода шаблона трехмерного графика.

Пример 1.10.Построить две объемные параболы, пересекающиеся в пространстве, и отформатировать их для придания наглядности рисунку. Зададим уравнения парабол функциями пользователя:

z1(x,y) := x² + y² - 20 z2(x,y) := -(x² + y²) + 20

Укажем их имена в шаблоне поверхности и, используя окно форматирования, выберем построение поверхностей с функциональной окраской. Заметим, что каждая поверхность может форматироваться отдельно. Полученный рисунок представлен на рис. 1.12.

Рис. 1.12. Построение двух пересекающихся в пространстве объемных парабол (вращая график мышью, можно рассмотреть его с разных сторон), а в окне форматирования графика выбрать разные схемы освещения

Окно форматирования трехмерной графики позволяет строить графики в нескольких системах координат, например, в сферической и цилиндрической системах координат. Сферическая система координат применяется в картографии, например, при построении карт на шаре - глобусе. Вид трехмерных графиков очень сильно зависит от того, в каких координатах строится график.

Для более детального знакомства с обширными возможностями визуализации геометрических понятий и результатов математических вычислений рекомендуется ознакомиться с литературой [5, 7] и примерами из справки по системе Mathcad.