Н.Г. Розенко Взаимозаменяемость, стандартизация и технические изменения
.pdf
20
Схемы расположения полей допусков для обычных гладких цилиндрических сопряжений приведены на рис. 13б и 14б.
а - для сопряжения вала с внутренним кольцом подшипника; б - для сопряжения вала с обычным основным отверстием
а - для сопряжения отверстия с наружным кольцом подшипника; б - для сопряжения отверстия с обычным основным валом
Подшипниковые посадки и соответствующие им посадки обычных гладких цилиндрических деталей различаются получающимися в сопряжении зазорами и натягами (табл. 2).
Анализ табл. 2 показывает, что замена поля допуска внутреннего кольца подшипника на поле допуска основного отверстия для обычных гладких цилиндрических сопряжений приводит к изменению характера
посадки: подшипниковая посадка k5 - с натягом, а посадка Hk 55 - пере-
ходная. Замена поля допуска наружного кольца подшипника на поле допуска обычного основного вала приводит к изменению характеристик посадки ( в данном случае - величины зазоров).
21
Таблица 2 Зазоры и натяги в сопряжениях с подшипниками качения и для обыч-
ных гладких цилиндрических деталей
|
|
|
|
|
|
|
|
|
|
|
До- |
Обозначение по- |
Характер |
Зазоры, мкм |
|
Натяги, мкм |
|
пус- |
|||||
садки |
посадки |
|
|
|
|
|
|
ки |
|||
|
|
|
|
|
|
|
|
|
|
|
по- |
|
|
|
|
|
|
|
|
|
|
|
сад- |
|
|
|
|
|
|
|
|
|
|
|
ки |
|
|
|
|
|
|
|
|
|
|
|
TS |
|
|
|
|
|
|
|
|
|
|
|
(TN), |
|
|
|
|
|
Smax |
Smin |
Sm |
Nmax |
Nmin |
Nm |
мкм |
|
|
|
к5 |
с натягом |
--- |
--- |
--- |
21 |
2 |
11,5 |
19 |
(подшипниковая) |
|
|
|
|
|
|
|
|
|||
|
H 5 |
переход- |
9 |
--- |
--- |
13 |
--- |
2 |
22 |
||
|
|
|
(обычная) |
ная |
|
|
|
|
|
|
|
|
k 5 |
|
|
|
|
|
|
|
|||
|
|
|
G6 |
с зазором |
44 |
12 |
28 |
--- |
--- |
--- |
32 |
(подшипниковая) |
|
|
|
|
|
|
|
|
|||
|
G6 |
с зазором |
56 |
12 |
34 |
--- |
--- |
--- |
44 |
||
|
|
(обычная) |
|
|
|
|
|
|
|
|
|
|
h6 |
|
|
|
|
|
|
|
|
||
Задача № 5
1.Изобразить графически поля допусков болта и гайки для метрической резьбы.
2.Найти по стандарту номинальные размеры трех диаметров резьбы, предельные отклонения и указать их на графическом изображении. Подсчитать предельные размеры диаметров, допуски диаметров.
3.Построить схему проверки резьбы болта и гайки предельными рабочими резьбовыми и гладкими калибрами. На схеме указать:
а) профиль болта и отдельно профиль гайки с полями допусков по трем диаметрам;
б) контуры профиля рабочих калибров с расположением их на границе контролируемого элемента резьбы;
в) предельные размеры диаметров заданной резьбы, контролируемые каждым калибром.
Методические указания к задаче № 5 1. Предельные контуры резьбового соединения с полями допусков
H
его элементов для скользящей посадки h показаны на рис. 15.
22
Рис. 15. Предельные контуры резьбового соединения метрической резьбы
2. По ГОСТ 24705-81 (СТ СЭВ 182-75) в зависимости от нормального диаметра и шага определить значения наружного d ( D) , среднего d 2( D2) , внутреннего d1( D1) диаметров резьбы, указать их на графиче-
ском изображении резьбового сопряжения.
По ГОСТ 16093-81 (СТ СЭВ 640-77) определить предельные отклонения трех диаметров и указать их на графическом изображении резьбового соединения.
Подсчитать предельные размеры и допуски трех диаметров по известным формулам
D2(D1) max = D2(D1) + ESD2(D1); |
(26) |
D2( D.D1 )min = D2( D.D1 ) + EJ D 2( D.D1) ; |
(27) |
d 2(d,d1) max = d 2(d,d1) +esd 2(d , d1); |
(28) |
d 2(d) min = d 2(d) + eid 2(d ); |
(29) |
TD2(TD1) = ESD2( D1) − EJD2(D1); |
(30) |
Td 2(Td ) = esd 2(d ) −eid 2(d ). |
(31) |
Величины ESD,eid1, D, d1min,TD,Td1 не нормируются.
3. Схема проверки резьбы болта и гайки предельными рабочими резьбовыми и гладкими калибрами изображена на рис. 16.
|
|
|
23 |
|
|
|
4 H 5H |
Пример |
|
Для резьбы |
M 20 |
p=2,5 мм выполнить действия, предусмот- |
||
6h |
||||
|
|
|
ренные в задаче № 5.
Для заданного резьбового соединения строим графическое изображение полей допусков (рис. 15).
Рис. 16. Схема проверки резьбы калибрами: а - болта; б - гайки
По ГОСТ 24705-81 (СТ СЭВ 182-75) выписываем значения параметров заданной резьбы:
d(D) = 20мм, d 2(D2) =18,376мм, d1(D1) =17,294мм.
Указываем их на схеме расположения полей допусков (рис.15).
По ГОСТ 16093-81 (СТ СЭВ 640-77) выписываем предельные отклонения диаметров резьбы (табл. 3) и указываем их на схеме расположения полей допусков (рис. 15).
Рассчитываем предельные размеры и допуски диаметров по форму-
лам (26) и (31).
24
Таблица 3 Предельные отклонения деталей резьбового соединения
Наименование |
Предельные отклонения |
Предельные отклонения |
||||
отклонения |
диаметров гайки, мкм |
диаметров болта, мкм |
||||
|
D |
D2 |
D1 |
d |
d2 |
d1 |
Верхнее |
--- |
+140 |
+355 |
0 |
0 |
0 |
Нижнее |
0 |
0 |
0 |
-335 |
-170 |
--- |
D2 max = D2 + ESD2 =18,376 +0,140 =18,516мм, D2 min = D2 + EJD2 =18,376 +0 =18,376мм,
D1 max = D1 + ESD1 =17,294 +0,355 =17,649мм, D1 min = D1 + EJD1 =17,294 +0 =17,294мм,
D min = D + EJD = 20,0 +0 = 20,0мм,
D max - не нормируется,
d 2 max = d 2 +esd 2 =18,376 +0 =18,376мм,
d 2 min = d 2 +eid 2 =18,376 +(−0,170) =18,206мм, d max = d +esd = 20,0 +0 = 20,0мм,
d min = d +eid = 20,0 +(−0,335) =19,665мм, d1 max = d1 +esd1 =17,294 +0 =17,294мм,
d1 min - нормируется,
TD2 = ESD2 − EJD2 = 0,140 −0 = 0,140мм, TD1 = ESD1 − EJD1 = 0,355 −0 = 0,355мм,
TD - не нормируется,
Td1 = esd 2 −eid 2 = 0 −(−0,170) = 0,170мм,
Td = esd −eid = 0 −(−0,355) = 0,355мм,
Td1 - не нормируется.
Схему проверки деталей (болта и гайки) заданного резьбового соединения изобразить, руководствуясь рис. 16. На схеме указать конкретные значения параметров заданной резьбы.
Задача № 6 Студенты, имеющие зачетные книжки, номера которых оканчива-
ются на цифры от 00 до 49, по заданным отклонениям замыкающего звена определяют отклонения составляющих звеньев (прямая задача), а студенты, зачетные книжки которых оканчиваются на цифры от 50 до
25
99, по заданным отклонениям составляющих звеньев определяют отклонения замыкающего звена (обратная задача).
Методические указания к задаче № 6
Прямая задача При решении прямой задачи целью расчета является определение
допусков и предельных отклонений составляющих размеров по заданным номинальным размерам замыкающего звена.
Порядок расчета следующий:
1. Определяется среднее число единиц допуска. При решении методом максимума-минимума
am = |
|
TA∆ |
, |
(32) |
|
m=1 |
|
|
|||
|
∑(0,453 |
D +0,001D) |
|
||
|
|
|
|||
j=1
где TA∆ - допуск замыкающего звена, мкм; m - общее число звеньев размерной цепи.
При решении теоретико-вероятностным методом
am = |
TA∆ |
. |
(33) |
|
D + 0,001D) λ2 j |
||||
m=1 |
|
|||
t∆ ∑(0,453 |
|
|
||
j =1 |
|
|
|
В знаменателе формул (32) и (33) приведена сумма единиц допусков составляющих размеров. Значения единиц допуска для размеров до 500 мм приведены в литературе [2, с.256].
Коэффициент риска t∆ выбирается в зависимости от принятого риска Ряд значений коэффициента Р, приведен ниже.
Риск, Р% 32,00 10,00 4,50 1,00 0,27 0,110 0,01 Коэффициент 1,00 1,65 2,00 2,57 3,00 3,29 3,89
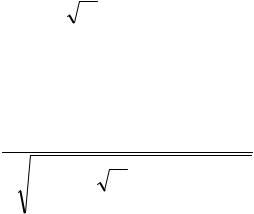
При нормальном законе распределения коэффициента λ2 j =1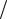
9, при законе распределения Симпсона (треугольника) λ2 j =1
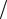5 при законе равной вероятности λ2 j =1
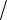3.
2.В зависимости от am выбирается ближайший квалитет [с.4,43,
табл. 18].
3.По ГОСТ 25346-89 (СТ СЭВ 145-88) находятся допуски состав-
26
ляющих звеньев. Для увеличивающих размеров отклонения назначаются как для основных отверстий, для уменьшающих - как для основных валов.
Правильность решения прямой задачи проверяют решением обратной задачи - для назначенных допусков должны выполняться следующие соотношения:
а) при решении методом максимума-минимума
m=1 |
|
∑TAj ≤TA∆, |
(34) |
j=1 |
|
б) при решении теоретико-вероятностным методом |
|
m=1 |
|
t∆ ∑λ2 j TA2 j ≤TA∆. |
(35) |
j=1 |
|
Пример Для сборочной единицы (рис.17) по заданным номинальным значе-
ниям составляющих звеньев цепи и параметрам замыкающего звена
A1=130 мм, A2=90 мм, A3=15 мм, A4=189 мм, A ∆=1±0,128 мм.
Определить допуски составляющих звеньев.
Допуск замыкающего звена исходя из заданных предельных отклонений
TA∆ = 0,56 мм = 560 мкм.
Определяем среднее число единиц допуска:
а) при решении методом максимума-минимума по формуле (32)
am = |
560 |
=57,4; |
2,56 +2,17 +2 1,08 +2,90 |
б) при решении теоретико-вероятностным методом по формуле (33) принимаем Р =0,27%, для которого t∆ =3,00 ; закон распределения составляющих звеньев - нормальный, в этом случае
am = |
|
|
|
|
560 |
|
|
|
|
=119,9. |
||
1 |
|
|
2 |
|
2 |
|
|
2 |
|
2 |
||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
3 |
|
|
2,52 |
|
+ 2,17 |
|
+ 2 |
1,08 |
|
+ 2,98 |
|
|
9 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27
Рис 17. Схема размерной цепи
Найденное число единиц допуска находится между 9-м и 10-м квалитетами при решении методом максимума-минимума и между 11-м и 12-м квалитетами при решении теоретико-вероятностным методом. Поэтому часть допусков назначается по более грубому квалитету, а часть - по более точному, но так, чтобы выполнялись соотношения (34) и (35). Результаты расчетов приведены в табл. 4.
Суммирование назначенных допусков составляющих размеров по формулам (34) и (35) и сравнение с заданным допуском замыкающего размера показывают правильность решения задачи:
m−1
∑TAj =160 +140 + 2 70 +115 = 555 < TA∆ = 560;
j =1
t∆ |
m∑−1(λ2 j TA2 j )=3 |
1 |
(2502 |
+3502 +2 1102 +2902 )=542 ≤TA∆ =560. |
|
j=1 |
9 |
|
|
Из анализа табл. 4 видно, что применение теоретиковероятностного метода расчета размерных цепей позволяет значительно расширить допуски на составляющие звенья при ничтожно малом риске выхода размеров замыкающего звена за допустимые пределы.
28
Обратная задача Решением обратной задачи проверяется степень рациональности
простановки размеров на чертеже, а также правильность назначения допусков и предельных отклонений составляющих размеров при решении прямой задачи.
При решении задачи методом максимума-минимума порядок расчетов следующий:
1) определяется нормальный размер замыкающего звена
n |
n+p |
|
A∆ = ∑AjYB − ∑AjYM; |
(36) |
|
j=1 |
j=n+1 |
|
где n - число увеличивающих размеров; p - число уменьшающих размеров;
2) определяются предельные размеры замыкающего звена
n |
n+p |
|
A∆ max = ∑AjYB.max − ∑AjYM.min; |
(37) |
|
j=1 |
n+1 |
|
n |
n+p |
|
A∆ min = ∑AjYB.min − ∑AjYM .max; |
(38) |
|
j=1 |
n+1 |
|
3) определяются предельные отклонения замыкающего звена |
|
|
ES (A∆)= A∆ max − A∆; |
|
(39) |
Ei(A∆)= A∆ min − A∆; |
|
(40) |
4) определяется допуск замыкающего звена |
|
|
n−1 |
|
|
TA∆ = ∑TAj. |
|
(41) |
j=1
При решении задачи теоретико-вероятностным методом порядок расчетов следующий:
1)расчет нормального размера замыкающего звена производится по формуле (36);
2)определяются координаты середин полей допусков составляющих звеньев
Ec( Aj) = |
1 |
[ES(Aj )+ EJ (Aj )]; |
(42) |
|
2 |
|
|
3) определяется координата середины поля допуска замыкающего звена
29
n |
n+ p |
|
Ec( A∆) = ∑Ec(Aj )YB − |
∑Ec(Aj )YM ; |
(43) |
j=1 |
j=n+1 |
|
4) определяется допуск замыкающего звена |
|
|
m−1 |
|
|
TA∆ = t∆ ∑λ2 j TAj ; |
|
(44) |
j=1
5)определяются предельные отклонения замыкающего звена
ES(A∆)= Ec(A∆)+ |
TA∆ |
; |
(45) |
||
|
|
||||
2 |
|
|
|
||
EJ (A∆)= Ec(A∆)− |
TA∆ |
|
; |
(46) |
|
|
|||||
2 |
|
|
|
||
6) определяются предельные размеры замыкающего звена |
|
||||
A∆ max = A∆ + ES (A∆); |
|
(47) |
|||
A∆ min = A∆ + EJ (A∆). |
|
(48) |
|||
После решения обратной задачи расчета размерных цепей сравнивают полученные в результате вычисления предельные размеры и допуск замыкающего звена с заданными их значениями исходя из функционального назначения сборочной единицы, машины или механизма и делают выводы о правильности назначения допусков составляющих звеньев.
Пример
Определить предельные значения и допуск замыкающего звена A∆ (рис. 17) по заданным предельным размерам составляющих звеньев:
A1 =130H8, A2 = 60H12, A3 =15e9, A4 =159h8.
Звенья A1 и A2 - увеличивающие, а звенья A3 и A4 - уменьшающие. Определяем номинальный размер замыкающего звена по формуле
(35)
A∆ = (130 +60)−(215 +159)=1мм.
По ГОСТ 25347-82 (СТ СЭВ 144-75) находим предельные отклонения составляющих звеньев:
A1 =130+0,063 , A 2 = 60 +0 , 300 , |
A3 |
=15−0,032 |
, |
A4 =159 |
. |
|
|
−0,075 |
|
|
−0,063 |
Решение задачи методом максимума-минимума
Предельные размеры замыкающего звена определяем по формулам
(37) и (38):