
В.А. Тесля Многоэтажные промышленные здания
.pdf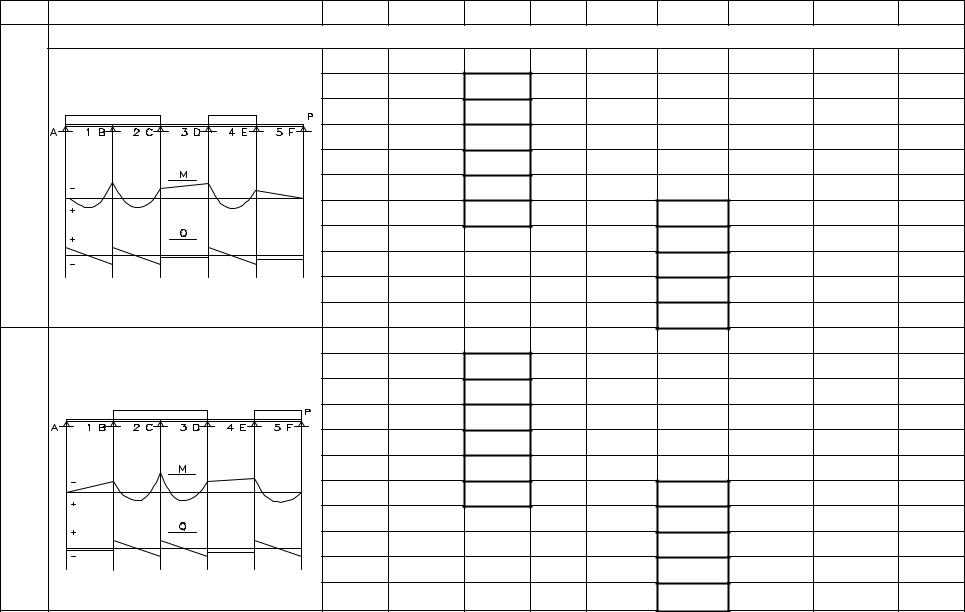
Продолжение табл.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
Отыскание максимальных отрицательных моментов |
|
|
|
|||||
|
|
МА |
0 |
0 |
|
|
|
|
|
|
|
|
М1 |
+0,065 |
106,704 |
|
|
|
+106,704 |
|
|
Загружение |
|
МВ |
-0,120 |
-196,992 |
|
|
|
-196,992 |
|
|
|
М2 |
+0,054 |
88,646 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
МС |
-0,022 -134,611 |
|
|
|
|
|
|
|
|
|
М3 |
-0,033 |
-54,173 |
|
|
|
|
|
|
4 |
|
МD |
-0,044 |
-72,230 |
QA |
+0,380 |
103,968 |
|
|
|
|
|
|
|
QВ1 |
-0,620 |
-169,632 |
|
-169,632 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
QВ2 |
0,598 |
163,613 |
|
+163,613 |
|
|
|
|
|
|
QС2 |
-0,402 -109,987 |
|
|
|
|
|
|
|
|
|
QС3 |
-0,196 |
-53,626 |
|
|
|
|
|
МА |
0 |
0 |
|
|
|
|
|
|
|
|
М1 |
-0,0175 |
-28,728 |
|
|
|
|
|
|
|
|
МВ |
-0,035 |
-57,456 |
|
|
|
|
|
|
Загружение5 |
|
М2 |
+0,052 |
85,363 |
|
|
|
|
|
|
|
МС |
-0,111 -182,218 |
|
|
|
-182,218 |
|
|
||
|
|
|
|
|
|
|
||||
|
|
М3 |
+0,0595 |
97,675 |
|
|
|
+97,675 |
|
|
|
|
MD |
-0,020 |
-32,832 |
QA |
-0,035 |
-9,576 |
|
|
|
|
|
|
|
|
QВ1 |
-0,035 |
-9,576 |
|
|
|
|
|
|
|
|
QВ2 |
+0,424 |
116,006 |
|
|
|
|
|
|
|
|
QС2 |
-0,576 |
-157,594 |
|
-157,594 |
|
|
|
|
|
|
QС3 |
0,591 |
161,698 |
|
+161,698 |
|
31
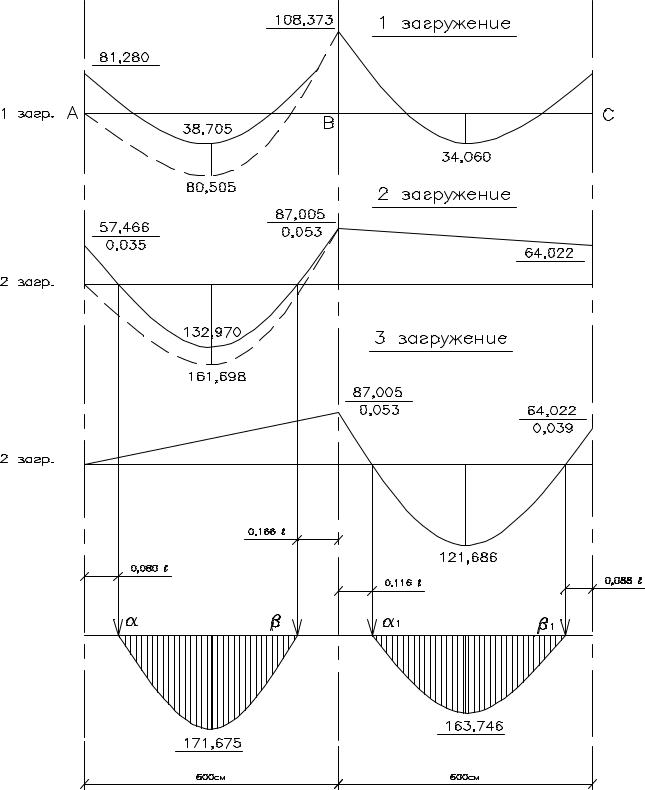
Суммирование ординат эпюр при отыскании максимальных положительных моментов приведено на рис. 16.
Рис.16. Суммирование эпюр положительных моментов
32
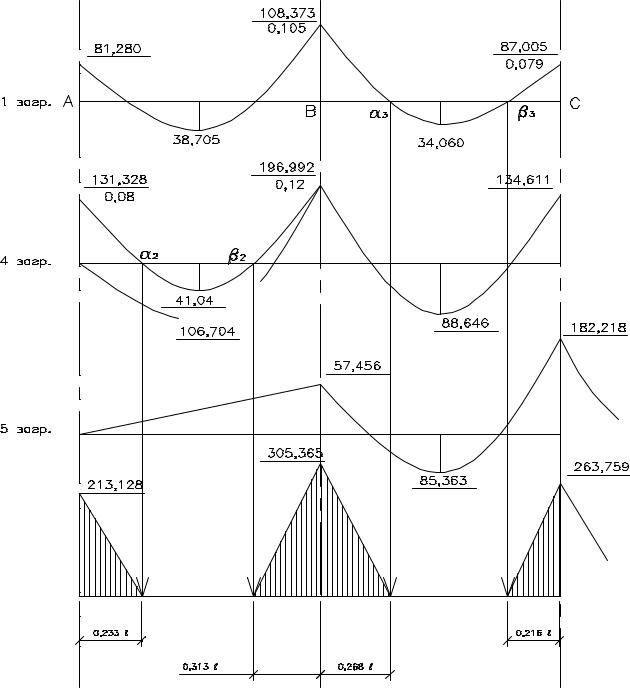
Суммирование ординат эпюр при отыскании максимальных отрицательных моментов приведено на рис. 17.
Рис.17. Суммирование эпюр отрицательных моментов
При построении эпюр как максимальных положительных, так и отрицательных моментов потребуется определение точек с нулевыми значениями моментов. На рис. 16 и 17 эти точки обозначены a, a1 и a2, а
33
также b, b1 и b2. Для отыскания положения точек составляется аналитическое выражение изменения моментов по длине балки. Это
|
p l |
|
|
x |
|
2 |
|
p x2 |
|
|
|
выражение имеет вид: |
|
x− ki ± |
ki+ 1 |
|
|
p l |
|
− |
|
= |
0. Перед вторым |
2 |
|
|
2 |
||||||||
|
|
|
l |
|
|
|
|
|
|||
слагаемым выражение в скобках принимает знак “+” при “возрастающем” моменте на правой опоре и “–“ при “убывающем”. Коэффициент ki+1 принимается как разница между предыдущим и последующим значениями коэффициентов. Так, для отыскания положений точек a и b по второму загружению, выражение после сокращения на “p” будет иметь вид:
lx − |
|
+ |
|
x |
2 |
− |
|
2 |
= 0. |
|
2 0,035 |
0,018 |
|
l |
|
x |
|
||||
|
|
|
||||||||
|
|
|
|
l |
|
|
|
|
|
|
Решение дает значения: x1 = 0,884l, x2 = 0,080l. Таким образом, расстояние от левой опоры до точки a будет равно 0,080l, а до точки b от правой опоры (1− 0,884)l = 0,166 l. В скобках принят знак “+”, т.к. на правой опоре kпр= 0,053 (момент возрастает по сравнению с левой опорой) – kлв= 0,035. А величина 0,018 = 0,053 – 0,035. Подобным образом определены все остальные расстояния.
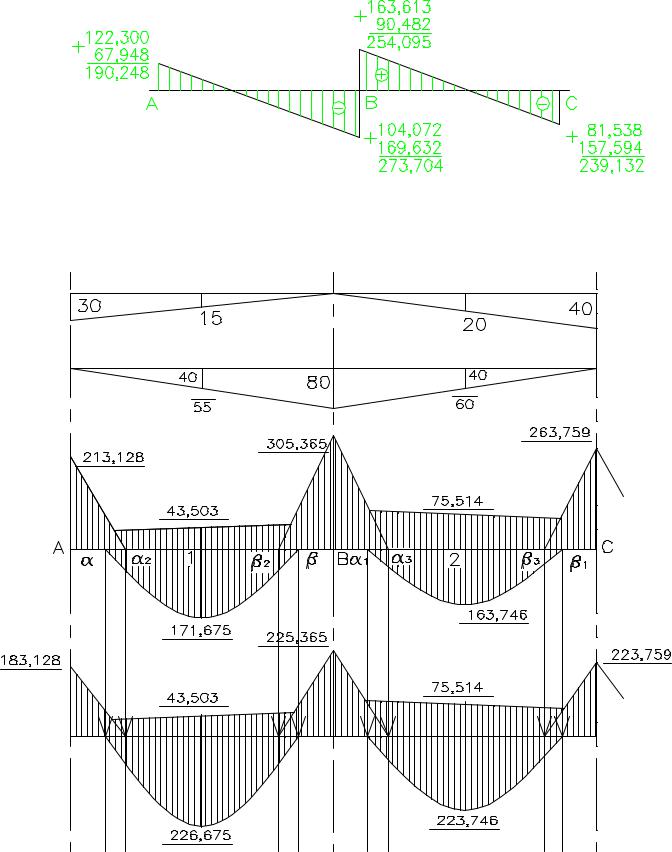
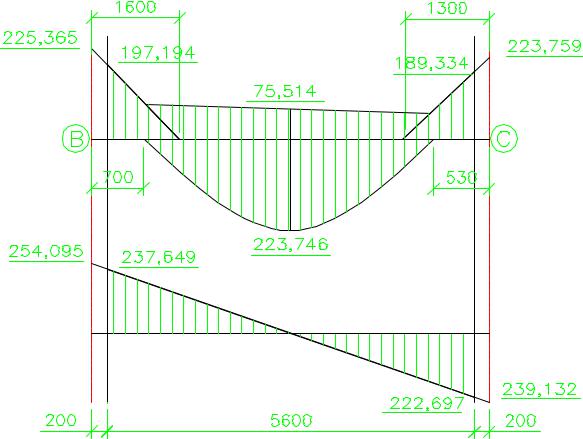
После построения эпюр с максимальными значениями +Мmax и –Mmax необходимо произвести выравнивание их значений. Для этого к найденным величинам прибавляют дополнительные треугольные эпюры положительных моментов таких значений, чтобы опорные и пролетные моменты по своей величине были примерно равны и составляли не менее 70% их максимальных значений, определенных ранее по упругой схеме. Это решение показано на рис. 19, где снижение моментов составляет на опоре А – 14%, на опоре В – 16% и на опоре С – 15%, что ниже допустимой величины 30%. Условие удовлетворяется. Отыскание максимальных значений поперечных сил производится обычным суммированием значений от действия постоянной нагрузки и одного из максимальных значений от временной нагрузки, как это показано на рис. 18.
34
Рис.18. Отыскание максимальных значений поперечных сил
Рис.19. Расчетная огибающая эпюра моментов ригеля
35
5.4. Расчет и конструирование ригеля второго пролета. Расчетные усилия М и Q для второго пролета приведены на рис. 20. Так как определение усилий производилось по величине пролета, равного расстоянию между осями – 6 м, что не соответствует истинной длине ригеля, определяем усилия по внутренним граням колонн.
Рис.20. Расчетные усилия М и Q
Конструирование стыка ригеля с колонной и расчет стыковых соединений с армированием ригеля в опорной части при бетоне В30 (gb2 = = 0,9) производится в следующем порядке:
1.Принимается конструктивное решение узлового соединения ригеля с колонной.
2.Определяется усилие в соединительных стержнях узла и по усилию подбирается их диаметр.
3.Расчетом определяются размеры закладной детали соединения ригеля с консолью колонны, см. рис. 21.
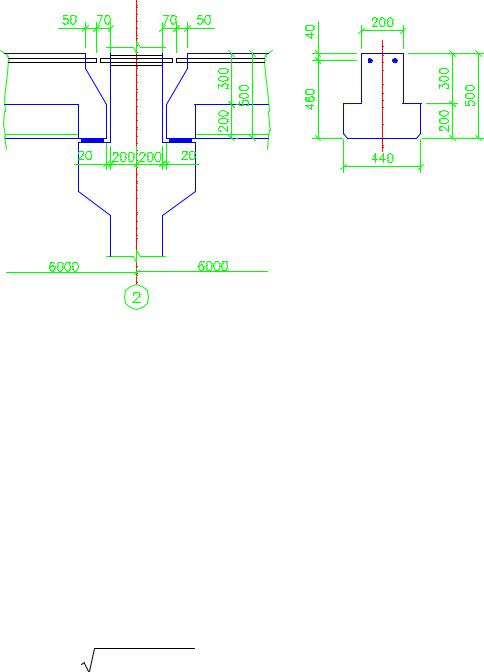
36
Рис.21. Узловое соединение ригеля с колонной
Решение:
1. Определяем усилие NS = M / z = 197,194 / 0,46 = 428,683 кН .
2.Подбираем диаметр соединительных стержней из арматуры класса АIII (RS = 365МПа) . Площадь поперечного сечения арматуры составит
A = |
N |
S |
/ R |
S |
= 428683/ 365 (100) = 11,74 см2. Принимаем 2 28, |
тогда |
S |
|
|
|
|
||
AS , fact = 12,32 см2. |
|
|||||
3. Размеры |
опорной закладной детали определим из условия смятия |
|||||
Q ≤ ψ |
Rb,los |
Alos1– формула (194)[3].Принимаем ψ = 0,75, Rb,los = α |
ϕ b Rb , |
|||
здесь α = 1, ϕ b = 3 Alos2 / Alos1 , где Alos2 – площадь консоли подошвы (40× 20) см, а Аlos1 – площадка смятия (размер площадки нашей
закладной) (20× 12) см. Для нашего случая, см. п. 3,94 [3] |
ϕ b = 1, т.к. |
принимается Alos2 = Alos1. Тогда выражение ψ Rb,los Alos1 = |
0,75 15,5× |
× (100)240 = 279000 Н, что больше Q fact = 237649 Н . Условие удовлетворяется.
Подбор арматуры ригеля и конструирование каркасов.
37
Определяем арматуру в середине пролета ригеля, сначала по величине положительного момента М = 223,746 кН м, потом по отрицательному моменту М = 75,514 кН м. В последнем случае ширина сечения принима-
ется равной b f = |
|
44 см. Решение производим в следующем порядке. |
|
|||||
Бетон– В30, |
γ |
b2 |
= 0,9, R |
= 15,5 МПа, R |
= 1,10 МПа , E |
b |
= 29 103 |
МПа |
|
|
b |
bt |
|
|
|
||
и α R = 0,413. |
При расчете по второй группе предельных состояний |
|||||||
Rb,ser = 22 МПа, Rbt ,ser = 1,80 МПа.Рабочая продольная арматура класса АIII, Rs = 365 МПа, Es = 200 103 МПа,поперечную арматуру из условий свариваемости с продольной арматурой диаметром 28 мм (см. расчет опорного
узла) принимаем диаметром не меньше 8 мм АIII, |
с Rsw = |
285 МПа . |
||||||||||
Коэффициент α = |
Es / Eb = 6,97 . |
|
|
|
|
|
||||||
Определяем требуемое количество арматуры по М = 223,746 кН м. На- |
||||||||||||
ходим: α |
m |
= M / R |
b h2 |
= 223,746 105 /15,5 (100) 20 452 |
= 0,052< α |
R |
= 0,413. |
|||||
|
|
|
b |
0 |
|
= |
|
|
|
|
||
По α |
m из табл. 21 [3] находим η |
0,768. Тогда потребное количество арма- |
||||||||||
туры |
будет |
равно: |
A = M / R |
h η = 223,746 105 / |
365 (100) 45 0,768= |
|||||||
|
|
|
|
|
|
s |
s |
0 |
|
|
|
|
= 17,74 см2 . По сортаменту принимаем 4 25 с A |
= |
19,63 см2 |
. Процент |
|||||||||
|
|
|
|
|
|
|
|
s,fact |
|
|
|
|
армирования µ |
= As,fact / b h0 = |
0,0218 или 2,18% < 2,5%, условие удовлетво- |
||||||||||
ряется.
Определяем требуемое количество арматуры по М = 75,514 кН м. Зна-
чение α |
m = 75,514 105 / 15,5 (100) 44 462 = 0,052< α |
R = 0,413. По am нахо- |
дим η = |
0,973. Тогда потребное количество арматуры As = M / Rs h0 η = |
|
= 4,62 см2 . По сортаменту принимаем 2 18 с A |
= 5,09 см2, что состав- |
|
|
s,fact |
|
ляет 0,25% армирования.
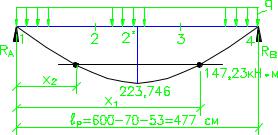
Конструируем каркас ригеля К–1, для чего потребуется определить длину дополнительного верхнего стержня при двухрядном армировании, см. рис. 22.
38
q = |
8 M = |
8 223,746 |
= |
78,67 кН/м |
||
|
|
l2p |
|
4,772 |
|
|
RA = RB = |
|
q l p |
= |
78,67 4,77 |
= 187,63 кН |
|
|
2 |
2 |
|
|||
Рис.22. Определение положения точек, где М = 147,23 кН м
|
Определяем величину момента при армировании ригеля 2 |
25 |
с |
||||||||||
A = |
9,82 |
см2. Находим ξ |
= µ |
Rs |
= |
9,82 |
365 = 0,246. По табл. 21 [3] при |
||||||
|
|
||||||||||||
s |
|
|
|
|
|
Rb |
20,47 15,5 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
ξ = |
0,246 значение α |
m |
= 0,215. Тогда момент будет равен M = R |
b h2 |
α |
m |
= |
||||||
|
|
|
|
|
|
|
|
b |
0 |
|
|
||
= 15,5 (100) 20 472 0,215= |
14722985 Н см = 147,23 кН м. Составляем урав- |
||||||||||||
нение q l |
x − q x2 = 147,23 |
кН м. При l = 4,77 м и q = 78,67 кН/м значения x1 |
|||||||||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
= 3,781 м, x2 = 0,989 м. Таким образом, длина дополнительного стержня будет равна x1 − x2 + 2 laн , где lан – длина зоны анкеровки, определяется по
формуле |
laн = (ω |
ан Rs / Rb + |
∆ λ ан) d , но не менее λ |
ан d = 20 d = 20 25= |
||||||
=500 мм, |
табл. 44 [3]. Табличные |
коэффициенты ω |
ан = |
0,70, ∆ λ ан = 11, |
||||||
λ |
ан = 20, |
при помощи |
которых |
определяем |
длину |
анкеровки lан = |
||||
= |
(0,70 365 / 15,5+ |
11) 25= |
687 мм, что больше |
λ ан d = |
500 мм . Условие |
|||||
удовлетворяется. |
Длина |
дополнительного |
стержня |
определяется |
||||||
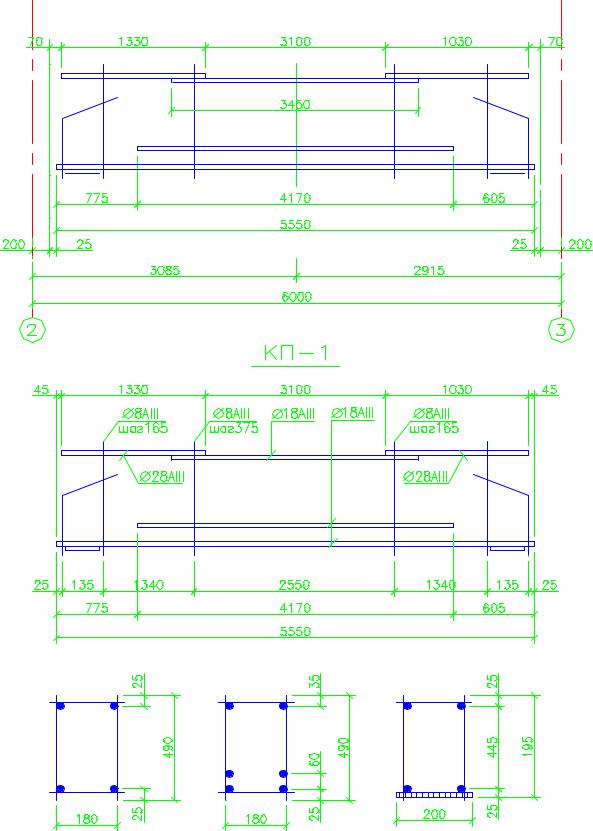
3781− 989 + 2 687 = 4166 мм . Принимаем длину дополнительного стержня 4170 мм. Все диаметры стержней их длины определены, можно конструировать каркас. Наглядность конструирования каркаса можно легко проследить на рис. 23.
39
Рис.23. Проектирование каркаса ригеля КП–1
