
ДМ_тест-экзамен
.pdf
|
|
|
|
тест |
|
|
|
Студент |
|
|
|
|
|||
|
|
|
|
Данные теста |
|
|
|
|
|
|
|
|
|
|
|
|
Автор |
Абатуров В.А., к.т.н. |
|
|
|
||
|
Заглавие |
Дискретная математика (Прикладная информатика 5 лет, 2 |
|||||
|
|
|
|
семестр (экзамен)) |
|
|
|
|
Выходные данные |
|
|
|
|
||
|
Количество вопросов |
36 |
|
|
|
||
|
Плановое время тестирования |
90 мин. |
|
|
|
||
|
Начало тестирования |
|
|
|
|
||
|
Окончание тестирования |
|
|
|
|
||
|
Фактическое время тестирования |
|
|
|
|
||
|
Попытка |
|
|
|
|
||
|
Результат |
баллов |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Вопросы теста |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
Выберите все правильные ответы |
|
|
|
|
|
|
Направление математики, изучающее свойства и отношения дискретных структур называют |
||||
|
|
|
|
|
|
|
|
|
|
|
|
Ответ |
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
дифференциальным исчислением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
непрерывной математикой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дискретной математикой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
финитной математикой |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
|
|
Выберите один правильный ответ |
|
|
|
Математическая теория наиболее общих свойств и отношений конечных и бесконечных совокупностей объектов, элиминирующая (игнорирующая) свойства самих объектов, называется
|
|
|
Ответ |
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
теорией алгоритмов |
|
|
|
|
|
|
|
|
|
|
|
|
|
теорией игр |
|
|
|
|
|
|
|
|
|
|
|
|
|
теорией кодирования |
|
|
|
|
|
|
|
|
|
|
|
|
|
теорией множеств |
|
|
|
|
|
|
|
|
|
|
|
|
|
теорией автоматов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
3 |
|
Выберите один правильный ответ |
|
|
|
|
|
|
Агрегатная точка зрения на первичное понятие «множество», |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ |
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
по аналогии с атрибутивной, является логически несостоятельной в том |
|
|
|
|
|
|
смысле, что она приводит к парадоксам (антиномиям) типа Рассела и |
|
|
|
|
|
|
Кантора. |
|
|
|
|
|
|
|
|
|
|
|
|
|
в отличие от атрибутивной, является логически несостоятельной в том |
|
|
|
|
|
|
смысле, что она приводит к парадоксам (антиномиям) типа Рассела и |
|
|
|
|
|
|
Кантора. |
|
|
|
|
|
|
|
|
|
|
|
|
|
по аналогии с атрибутивной, является логически состоятельной в том |
|
|
|
|
|
|
смысле, что она не приводит к парадоксам (антиномиям) типа Рассела и |
|
|
|
|
|
|
Кантора. |
|
|
|
|
|
|
|
|
|
|
|
|
|
в отличие от атрибутивной, является логически состоятельной в том |
|
|
|
|
|
|
смысле, что она не приводит к парадоксам (антиномиям) типа Рассела и |
|
|
|
|
|
|
Кантора. |
|
|
|
|
|
|
|
|
|
|
|
|
|
по аналогии с атрибутивной, является логически состоятельной в том |
|
|
|
|
|
|
смысле, что она не приводит к парадоксам (антиномиям) типа Рассела и |
|
|
|
|
|
|
Кантора. |
|
|
|
|
|
|
в отличие от атрибутивной, является логически состоятельной в том |
|
|
|
|
|
|
смысле, что она приводит к парадоксам (антиномиям) типа Рассела и |
|
|
|
|
|
|
Кантора. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
4 |
|
Выберите один правильный ответ |
|
|
|

|
Даны |
множества |
А |
{x |
С | x2 |
1 |
0}, |
В |
{x |
С | x4 |
1 |
0}, где С – множество |
||
комплексных чисел. Найти множество F такое, что |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
F |
В \ А |
|
|
|
|
|
|
|
|
|
|
|
Ответ |
|
|
|
|
|
|
Студента |
|
F |
{ |
j | j |
1} |
|
|
|
|
|
|
|
|
|
|
|
F |
{ j, |
j | j |
1} |
|
|
|
|
|
|
|
|
|
|
|
F |
{1, |
1, j | j |
1} |
|
|
|
|
|
|
|
|
|
|
|
F |
{1, |
1, j, |
j | j |
1} |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
Выберите один правильный ответ |
|
|
|||||
Определению «Множество А, каждый элемент которого является элементом другого множества М, |
||||||||||||||
называется подмножеством данного множества М» соответствует следующая символическая запись: |
||||||||||||||
|
|
|
|
|
Ответ |
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
|
(А М) ~ ((х А) (х М)) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
(А М) ~ ((х А) (х М)) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
(А М) ~ ((х А) (х М)) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
(А М) ~ ((х А) (х М)) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
Выберите все правильные ответы |
|
|
|
Графической интерпретацией множества А (надмножеством) может быть:
|
|
|
|
|
Ответ |
|
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
символическая запись А |
|
М |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
диаграмма Эйлера-Венна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
характеристическая функция (индикатор) fA(x): M |
{0,1} |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
В берите один правильный ответ |
|
|||
Индикатор (характеристическая функция) четкого отношения включения элементов множества А в элементы множества М fA(x): M {0,1} задается соотношением
Ответ |
|
Студента |
|
|
|
|
|
|
fA(x)= |
0, |
если x |
A |
|
|
|
|
|
|
|
|
|
|
|
0,1 , если x |
A |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
fA(x)= |
0,1 , если x |
A |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0, если x |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
fA(x)= |
0, если x |
A |
|
|
|
|
|
||
|
|
|
|
|
1, если x |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
fA(x)= |
1, если x |
A |
|
|
|
|
|
||
|
|
|
|
|
0, если x |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
Выберите один правильный ответ |
|
|||
|
|
|
Дано |
множество А = {x |
Z |
0 < x 12}, |
где Z – множество целых чисел. Найти множество В |
|
||||
|
|
|
такое, |
что В |
А и В = {x x делится на 4}. |
|
||||||
|
|
|
|
|
|
|
|
Ответ |
|
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
В = {2, 4, 6, 8, 10, 12} |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
В = {1, 3, 5, 7, 9, 11} |
|
|
|
|
|
|
|||
|
|
|
В = {0, 1, 2, 3, 5, 8} |
|
|
|
|
|
|
|||
|
|
|
В = {0, 4, 8, 12} |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
В = {4, 8, 12} |
|
|
|
|
|
|
|
||
|
|
|
В = {0, 4, 8} |
|
|
|
|
|
|
|
||
|
|
|
В = {4, 8} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 В = Ø
В = Ø
9 |
Выберите один правильный ответ |
|
Функция, переменные которой принимают значения из некоторого множества М, а сама функция |
|
принимает два значения: И (истина) и Л (ложь), т.е. |
|
|
|
|
|
|
|
|
|
|
P(x , x |
2 |
,..., x |
n |
) : M n |
{И , Л} |
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
называется |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Ответ |
|
|
|
|
|
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
высказыванием |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
квантором существования |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
квантором общности |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
предикатом |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
Выберите один правильный ответ |
|
|||||||
|
|
|
Квантором общности называется высказывание … |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ |
|
|
|
|
|
|
Студента |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
истинное, когда Р(х) истинно для каждого элемента х из множества М, и |
|
|
|
|||||||||||
|
|
|
|
ложное – в противном случае, и которое обозначается ( х)Р(х). |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
ложное, когда Р(х) истинно для каждого элемента х из множества М, и |
|
|
|
|||||||||||
|
|
|
|
истинное – в противном случае, и которое обозначается ( х)Р(х). |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
истинное, когда существует элемент из множества М, для которого Р(х) |
|
|
|
|||||||||||
|
|
|
|
истинно, и ложное в противном случае, и которое обозначается ( х)Р(х). . |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
ложное, когда существует элемент из множества М, для которого Р(х) |
|
|
|
|||||||||||
|
|
|
|
истинно, и истинное в противном случае, и которое обозначается ( х)Р(х). |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
Расставьте соответствие между ответами |
|
|||||||
|
|
|
Укажите соответствие |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Ответ |
|
|
|
|
|
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
перенос квантора через отрицание |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
вынесение квантора за скобки |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
перестановка одноименных кванторов |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
( x)(A(x) & B) ( x)A(x) & B; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
( y)( x)A(x,y) |
( |
x)( |
y)A(x,y); |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
( х)(А(х) & B) ( x)A(x) & B; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
( x)A(x) |
( x) A(x); |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
( y)( |
x)A(x,y) |
( |
x)( |
y)A(x,y); |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
Выберите один неправильный ответ |
|
|||||||
|
|
|
Какими бы ни были формулы А и В для них справедливы следующие аксиомы |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
Ответ |
|
|
|
|
|
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
(B |
A); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(A |
(B |
C)) |
|
((A |
B) |
(A C)); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( B |
A) |
(( |
B |
A) |
B); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
( xi)A(xi) |
A(xj), где формула А(хi) не содержит переменной xi. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
A(xi) |
( xj)A(xj), где формула А(хi) содержит переменную xi. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
Расставьте соответствие между ответами |
|
|||||||
|
|
|
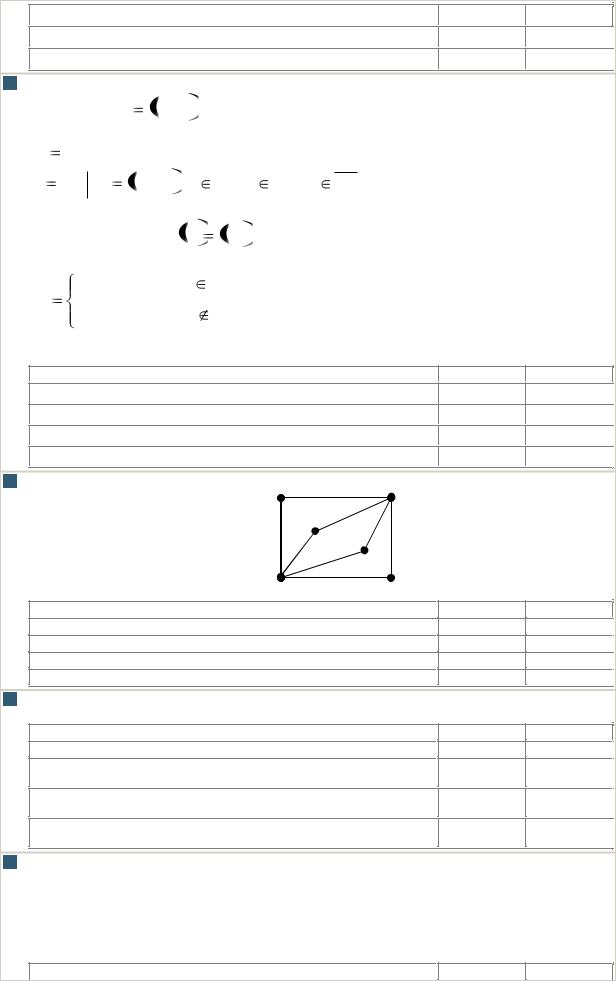
Даны булевы функции X1= {1, 1, 0, 0}и X2={1, 0, 1, 0}. Укажите соответствие между логическими |
|
||||||||||||||
|
|
|
операциями и их значениями |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ |
|
|
|
|
|
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1&X2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 X2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 |
X2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 |
X2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{0, 0, 1, 1} |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
{1, 0, 0, 0} |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{1, 0, 0, 1} |
|
|
|
|
|
||
{1, 0, 1, 1} |
|
|
|
|
|
||
{1, 1, 1, 0} |
|
|
|
|
|
||
14 |
|
|
|
|
Выберите один правильный ответ |
||
Задан орграф |
D |
Х , A , который представляет собой совокупность множества вершин |
|||||
Х |
{x1 |
, x2 , , xр } и упорядоченного множества пар вершин |
|||||
|
|
|
|
|
|
|
|
А {аij |
аij |
|
xi , x j , xi |
X , x j |
X , i, j 1, p} . |
||
|
|
|
|
|
|
порядка р , у которой |
|
Квадратичная матрица А D |
аij |
||||||
aij |
1, |
если (хi , х j ) |
А |
|
|
||
0, |
если (хi , х j ) |
А |
|
|
|||
|
|
|
|||||
называется |
|
|
|
|
|
||
|
|
|
|
|
Ответ |
|
Студента |
матрицей смежности вершин орграфа D |
|
|
|||||
матрицей инцидентности орграфа D |
|
|
|||||
матрицей смежности дуг орграфа D |
|
|
|||||
матрицей достижимости орграфа D |
|
|
|||||
15 |
|
|
|
|
Выберите все неправильные ответы |
||
В графе |
|
|
|
|
|
|
|
|
|
|
|
|
Ответ |
|
Студента |
есть и эйлеров и гамильтонов циклы |
|
|
|||||
есть эйлеров цикл, но нет гамильтонова |
|
|
|||||
есть гамильтонов, но нет эйлерова цикла |
|
|
|||||
нет ни эйлерова, ни гамильтонова цикла |
|
|
|||||
16 |
|
|
|
|
Выберите все правильные ответы |
||
Укажите все логические высказываниями, принимающие значение «истинно» |
|||||||
|
|
|
|
|
Ответ |
|
Студента |
Граф G называется деревом, если он является связным и не имеет циклов. |
|||||||
Граф G, все компоненты связности которого являются деревьями, |
|||||||
называется лесом. |
|
|
|
|
|||
У графа, который является деревом, число ребер на единицу больше |
|||||||
числа вершин |
|
|
|
|
|
||
Дерево содержит циклы, любые две его вершины нельзя соединить |
|||||||
единственной простой цепью |
|
|
|
||||
17 |
|
|
|
|
Выберите один правильный ответ |
||
Укажите, в каком случае логическое высказывание |
|||||||
«... – совокупность символов, указывающих операцию и значения, либо местонахождение, ее |
|||||||
элементов» |
|
|
|
|
|
||
принимает значение «истинно». |
|
|
|
||||
|
|
|
|
|
Ответ |
|
Студента |

|
|
|
|
|
Оператор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Программа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Директива |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Алгоритм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
Введите правильный ответ в каждую позицию |
|
|
|
||
|
|
|
|
После выполнения операторов |
|
|
|
|||||
|
|
|
|
const n=10; |
|
|
|
|
|
|
||
|
|
|
|
a:array[1..n]of byte=(2,1,0,3,5,0,4,3,5,7); |
|
|
|
|||||
|
|
|
|
var k,i:byte; |
|
|
|
|
|
|
||
|
|
|
|
begin |
|
|
|
|
|
|
||
|
|
|
|
k:=0; |
|
|
|
|
|
|
||
|
|
|
|
for i:=1 to n do |
|
|
|
|
|
|
||
|
|
|
|
if a[i]mod 3=2 then k:=k+a[i]; |
|
|
|
|
|
|
||
|
|
|
|
writeln(k); |
|
|
|
|
|
|
||
|
|
|
|
end. |
|
|
|
|
|
|
||
|
|
|
|
значение переменной К равно |
|
|
|
|||||
|
|
|
|
|
Ответ |
|
|
|
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
#1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.19 |
|
|
|
|
Выберите все правильные ответы |
|
|
|
|||
|
|
|
|
Для измерения информации вводятся показатели: |
|
|
|
|||||
|
|
|
|
|
|
|
Ответ |
|
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
количество информации; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
объем данных; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
длина сообщения; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
количество символов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
Выберите один правильный ответ |
|
|
|
||
Взаимно-однозначное соответствие при котором в двух системах, рассматриваемых отвлеченно от природы составляющих их элементов, справедливо, что каждому элементу первой системы соответствуют лишь один элемент второй и каждой связи в одной системе соответствует связь в другой, и обратно,
называется … |
|
|
Ответ |
|
Студента |
|
|
|
изоморфным |
|
|
|
|
|
гомоморфным |
|
|
|
|
|
эндоморфизмом алгебраической системы
Мономорфизмом группы
|
21 |
|
|
|
|
|
|
|
Введите правильный ответ в каждую позицию |
|
|
|
|||||
|
|
|
После выполнения оператора F:= A>=B над множествами А=[1,2,3,4,7,9] и В=[1,2,3] F получит значение |
|
|||||||||||||
. . . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ |
|
|
|
|
|
|
|
|
|
|
Студента |
|
||
|
|
|
|
#1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
Расставьте соответствие между ответами |
|
|
|
||
|
|
|
Бинарные функции можно записать в виде формул логики высказываний |
... |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ |
|
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z x1 |
x2 |
(x1 |
x2 ) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
x1 |
x2 |
|
|
x1 |
x2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
x1 |
х2 |
x1 |
x2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
штрих Шеффера – отрицание конъюнкции
стрелка Пирса – это отрицание дизъюнкции
сложение по модулю два представляет собой отрицание эквивалентности
23 |
Выберите один правильный ответ |
При входном потоке
1 строка 10 20 30 40
2 строка 50 60

после выполнения операторов
Var A,B,C,D:integer; Begin
read(A,B);
read(C);
readln(D);
переменная D получит значение ..
|
|
|
|
|
Ответ |
|
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
Выберите один правильный ответ |
|
|
|
|
|
|
|
Укажите, в каком случае логическое высказывание |
|
|
|
|
||
|
|
|
|
|
«Константа типа String занимает в памяти ... |
байт» |
|
||
|
|
|
принимает значение «истинно». |
|
|
|
|
||
|
|
|
|
|
Ответ |
|
|
Студента |
|
|
|
|
|
|
|
|
|||
|
|
|
|
255 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
8 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
128 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
256 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
Выберите все правильные ответы |
|
|
|
|
|
|
|
Укажите те и только те высказывания, совокупность которых дает истинное определение |
|
|||||
|
|
|
«Метрикой на множестве Е называется функция f(x, y), ..., …, ,…» |
|
|
|
|
||
|
|
|
|
|
Ответ |
|
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определенная на декартовом произведении Е Е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значениями которой являются положительные действительные числа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значениями которой являются неотрицательные действительные числа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
удовлетворяющая при любых значениях х, у, z из множества Е условию |
|
|
|
|
|
|
|
|
|
f(x, y) = f(y, x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
удовлетворяющая при любых значениях х, у, z из множества Е условию |
|
|
|
|
|
|
|
|
|
f(x, y) + f(y, x) |
f(x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
удовлетворяющая при любых значениях х, у, z из множества Е условию f(x, y) = 0 тогда и только тогда, когда х = у
удовлетворяющая при любых значениях х, у, z из множества Е условию f(x, y) ≥ 0 тогда и только тогда, когда х = у
удовлетворяющая при любых значениях х, у, z из множества Е условию f(x, y) ≠ 0 тогда и только тогда, когда х = у
|
26 |
|
|
|
|
|
|
|
|
|
|
|
Выберите один правильный ответ |
|
|
|
|
|
|
Была получена формула булевой функций в СДНФ |
|
|
|
||||||||||
|
|
|
Z = x1x2 x3 |
x1x2 x3 . |
|
|
|
|
||||||||
|
|
|
Укажите ее СКНФ: |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ |
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x1x2 x3 x1x2 x3 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1x2 x3 x1x2 x3 |
|
|
|
|
|
||||||
|
|
|
|
|
x1 |
x2 |
x3 x1 |
x2 |
x3 |
|
|
|
||||
|
|
|
|
|
x1 |
x2 |
x3 x1 |
x2 |
x3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
Введите правильный ответ в каждую позицию |
|
|
|
После выполнения операторов
. . . A:='ABCDEF';
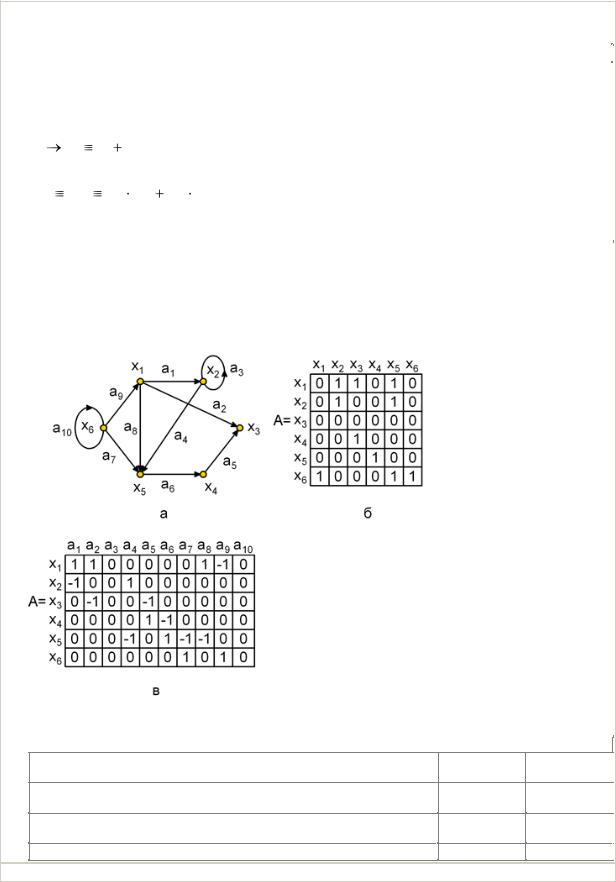
if A[1] in ['A'..'Z'] then F:=1 else F:=2; . .
значение F будет равно
|
|
|
Ответ |
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
#1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
28 |
|
|
Выберите один правильный ответ |
|
|
|
|
|
Указанные отношения алгебры логики |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
x2 |
x1 x2 . |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x1 |
x2 ) |
(x1 x2 ) (x1 x2 ) . |
|
|
|
|||||
|
|
|
называются |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ |
|
Студента |
|
|
|
|
|
|
|
|
|||||||
|
|
|
законами ассоциативности конъюнкции и дизъюнкции |
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
законами дистрибутивности |
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
Законами инверсии (де Моргана) |
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
правилами замены логических операций |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
|
|
|
|
|
|
|
|
Выберите один правильный ответ |
|
|
|
На рисунке представлены...
Ответ |
|
Студента |
а– неограф; б – матрица инциденций (матрица инцидентности); в – матрица смежности
а– орграф; б – матрица смежности; в – матрица инциденций (матрица инцидентности)
а– орграф; б – матрица инциденций (матрица инцидентности); в – матрица смежности
а – орграф; б – матрица достижимости; в – матрица смежности
30 |
Расставьте соответствие между ответами |
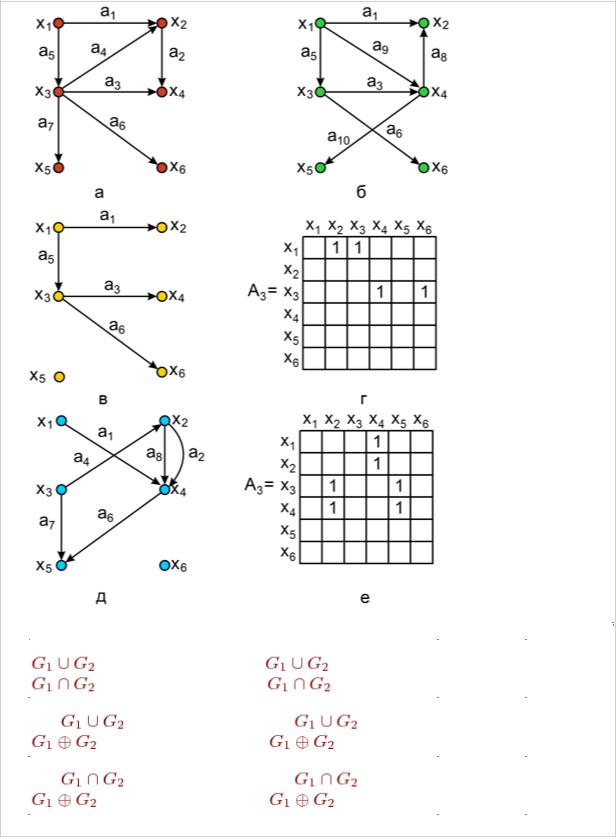
На рисунке представлены...
|
|
|
|
Ответ |
|
|
Студента |
|
|
|
|
|
|
||||
|
|
|
Операция объединения и пересечения: а – граф G1 ; б – граф G2 ; в – граф |
|
|
|
||
|
|
|
|
; г – матрица смежности графа |
; д – граф |
|
|
|
|
|
|
|
; е – матрица смежности графа |
|
|
|
|
|
|
|
|
|
||||
|
|
|
Операция объединения и кольцевой суммы: а – граф G1 ; б – граф G2 ; в – |
|
|
|
||
|
|
|
граф |
; г – матрица смежности графа |
; д – граф |
|
|
|
|
|
|
|
; е – матрица смежности графа |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Операция пересечения и кольцевой суммы: а – граф G1 ; б – граф G2 ; в – |
|
|
|
||
|
|
|
граф |
; г – матрица смежности графа |
; д – граф |
|
|
|
|
|
|
|
; е – матрица смежности графа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
31 |
|
|
Выберите один правильный ответ |
|
|||
|
|
|
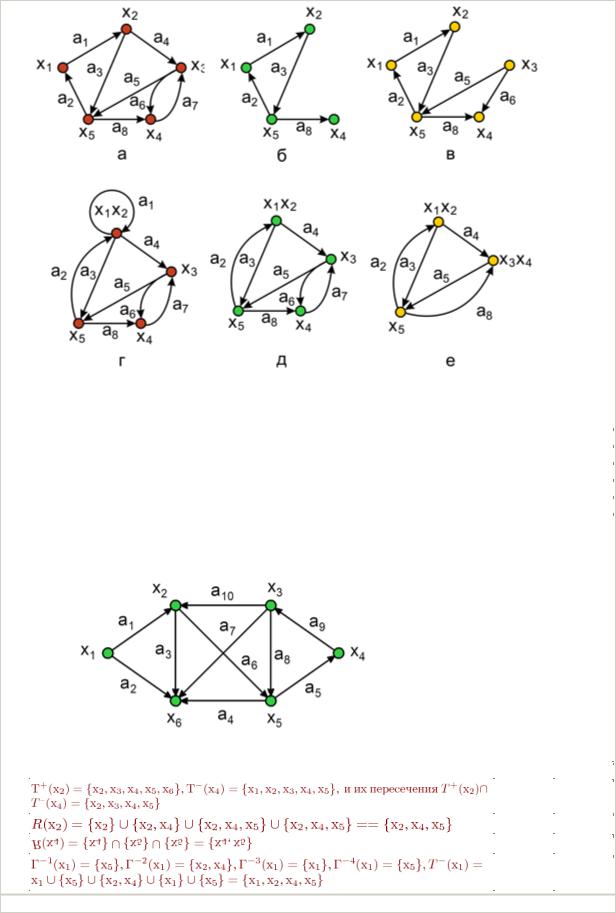
На каких из рисунков представлены операции «удаления дуг a4 и a7 » и |
|
|
||
|
|
|
«стягивания дуг a1 |
, a6 и a7» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ |
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
а) и д) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) и г) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) и е) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д) и е) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) и е) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
32 |
|
|
Выберите один правильный ответ |
|
|
|
Для данного орграфа нахождение вершин, входящих в путь из вершины х2 в вершину х4 сводится к нахождению
Ответ |
|
Студента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
Выберите один правильный ответ |
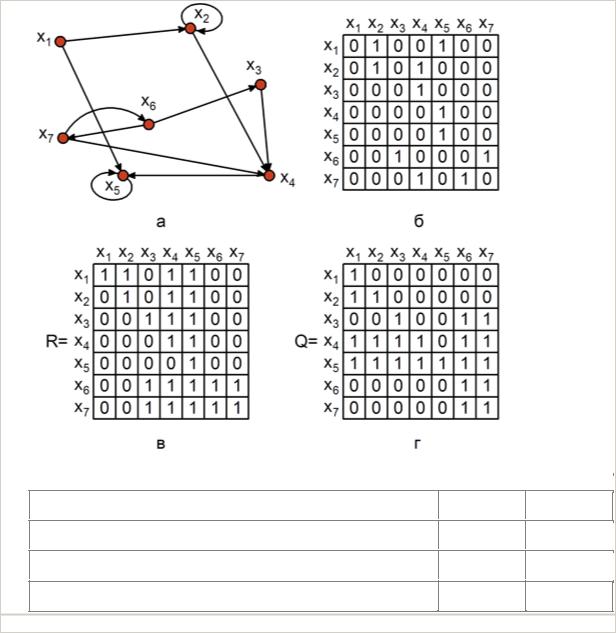
На рисунке представлены...
Ответ |
|
Студента |
|
|
|
а–граф; б – матрица смежности; в – матрица контрдостижимости; г- матрица достижимости
а–граф; б – матрица смежности; в – матрица достижимости; г- матрица контрдостижимости
а–граф; б – матрица достижимости; в – матрица смежности; г- матрица контрдостижимости
а–граф; б – матрица контрдостижимости; в – матрица смежности; г- матрица достижимости
34 |
Выберите один правильный ответ |
