
- •Математический практикум с применением пакета Mathcad
- •Оглавление
- •1. Введение в Mathcad
- •1.1. Интерфейс Mathcad
- •1.1.1. Главное меню Mathcad
- •1.1.2. Панели инструментов
- •2. Задачи элементарной математики
- •2.2. Построение графиков функций
- •2.3. Решение алгебраических уравнений и систем
- •3. Задачи линейной алгебры
- •3.1. Основные сведения о матричных операциях
- •3.2. Решение типовых задач по линейной алгебре
- •4. Задачи математического анализа
- •4.1. Вычисление пределов числовых последовательностей и функций
- •4.2. Исследование сходимости и вычисление сумм рядов
- •4.3. Дифференцирование функций одной переменной
- •4.4. Интегрирование функции одной переменной
- •4.4.1. Неопределенные интегралы
- •4.4.2. Определенные интегралы
- •5.1. Решение задачи Коши
- •5.1.1. Решение задачи Коши методом Эйлера
- •5.1.2. Решение задачи Коши методом Рунге–Кутта второго порядка
- •5.1.3. Решение задачи Коши методом Рунге–Кутта четвертого порядка
- •5.1.4. Решение задачи Коши при помощи встроенных функций
- •5.2. Решение краевой задачи
- •6. Теории вероятностей и математическая статистика
- •6.1. Дискретные случайные величины
- •6.2. Непрерывная случайная величина
- •7. Программирование в Mathcad
- •Заключение
- •Предметный указатель
- •Список литературы

5.2. Решение краевой задачи
Постановка краевой задачи
Пусть требуется найти функцию y=f(x), которая на сегменте (a, b) удовлетворяет дифференциальному уравнению
y// |
+ p(x) y/ + q(x) y = F(x) |
|
(5.6.) |
||||||
и смешанным граничным условиям |
|
||||||||
|
|
/ |
(a) + βa y(a) |
=γa |
, |
|
|||
αa y |
(5.7.) |
||||||||
|
|
y/ |
(b) + β |
|
y(b) |
=γ |
|
. |
|
α |
b |
b |
b |
|
|||||
|
|
|
|
|
|
|
|||
Граничные условия (5.7) являются универсальными. Для различных комбинаций коэффициентов αa , αb , βa и βb получаем
различные типы граничных условий. Так, при αa =αb = 0, βa = βb =1 получаем граничные условия, в которых заданы значения искомой функции на границе области: y(a) =γa , y(b) =γb . В случае, если αa =αb =1, βa = βb = 0, получаем граничные ус-
ловия, в которых на границе области заданы значения производной от искомой функции y′(a) =γa , y′(b) =γb.
Метод прогонки
Поставленную задачу (5.6), (5.7) удается решить в аналитическом виде только для некоторого достаточно узкого класса функций p(x), q(x) и f(x). В подавляющем большинстве практических задач для решения поставленной задачи используются численные методы. Для решения краевой задачи наиболее эффективным яв-
ляется метод прогонки.
Для простоты алгоритма введем на отрезке [a, b] равномерную сетку узлов x0=a, x1, x2, …, xn=b. Расстояние между соседними уз-
лами (шаг сетки) h = b −n a . Координаты i-го узла сетки опреде-
ляются по формулам xi = a + i h, i=0, 1, 2, …, n. Для краткости записей формул будем обозначать значения функций в узлах сетки именем функции с индексом, равным номеру узла. Например, f(xi) будем обозначать fi; p(xi) – pi , и так далее.
Перейдем теперь от дифференциальной задачи (5.6), (5.7), определенной в каждой точке отрезка [a, b] (таких точек бесконеч-
84
ное количество), к конечно-разностной задаче, определенной на конечном множестве точек, являющихся узлами сетки (n+1 точка). При переходе от непрерывной (5.6), (5.7) задачи к конечноразностной (дискретной) необходимо заменить производные функций при помощи конечно-разностных производных.
Выведем конечно-разностные формулы для первой и второй производных y′ и y′′. Для этого используем формулу Тейлора,
согласно которой функция y(x), непрерывная и дифференцируемая в некоторой точке x, может быть представлена в окрестности этой точки следующим образом:
y(x + h) = y(x) + |
y′(x) |
h + |
y′′(x) |
h2 + |
y′′′(x) |
h3 |
+ |
+ |
|
y(k) (ξ1) |
hk .(5.8) |
|||||||||||
|
|
|
|
|
3! |
|
||||||||||||||||
|
1! |
|
|
2! |
|
|
|
|
|
|
|
k! |
|
|
|
|||||||
Эта же формула для приращения –h имеет вид: |
|
|
|
|
||||||||||||||||||
|
|
|
′ |
|
|
′′ |
′′′ |
|
y |
(k) (ξ |
2 |
) |
|
|
||||||||
y(x − h) = y(x) − |
y (x) |
h + |
y (x) |
h2 − |
y |
(x) |
h3 + + |
|
|
|
|
(−h)k . |
||||||||||
|
|
|
3! |
|
|
k! |
|
|
||||||||||||||
|
1! |
|
|
2! |
|
|
|
|
|
|
|
|
|
|
(5.9) |
|||||||
В этих формулах ξ1,ξ2 (x −h, x + h). |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
Выражая из этих уравнений y′, |
получаем правую и левую ко- |
|||||||||||||||||||||
нечную разность для первой производной: |
|
|
|
|
|
|
|
|
||||||||||||||
y′ = |
y(x + h) − y(x) |
|
+O(h), |
|
|
|
|
|
|
|
|
|
(5.10) |
|||||||||
h |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y′ = |
y(x) − y(x −h) |
|
+O(h), |
|
|
|
|
|
|
|
|
|
(5.11) |
|||||||||
h |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где O(h) – погрешность аппроксимации, равная сумме отброшенных слагаемых.
Более точная формула получается, если из формулы (5.8) вычесть формулу (5.9) и разность разделить на 2h.
y′ = |
y(x + h) − y(x −h) |
+O(h2 ) . |
(5.12) |
|
2h |
||||
|
|
|
Эта формула называется центральной конечно-разностной производной и имеет второй порядок аппроксимации, т.е. вычисляет первую производную с точностью порядка h2.
Аппроксимацию второй производной можно получить, если сложить уравнения (5.8) и (5.9) и разделить на h2.
y′′ = |
y(x + h) −2y(x) + y(x −h) |
+O(h2 ) . |
(5.13) |
|
h2 |
||||
|
|
|
||
|
|
|
85 |

Эта формула аппроксимирует вторую производную с точностью порядка h2.
Вернемся теперь к решению краевой задачи (5.6), (5.7).
Для вычисления производной на левой границе области ис-
пользуем правую конечную разность y/ (a) = y1 −h y0 +O(h) .
Для вычисления производной на правой границе области ис-
пользуем левую конечную разность y′(b) = yn − yn−1 +O(h).
h
Для внутренних точек xi используем более точные центральные конечные разности:
y′(xi ) = |
yi+1 − yi+1 |
+O(hi ) ; |
y′′(x ) = |
yi+1 −2yi + yi−1 |
+O(h2 ) . |
|
2h |
h2 |
|||||
|
|
i |
|
После подстановки приведенных конечно-разностных производных в формулы (5.6), (5.7) для каждой узловой точки получаем систему n+1-го линейного уравнения с n+1-ым неизвестным y0, y1, …, yn.
α |
α |
|
|
y1 − y0 |
|
|
|
|
+β |
|
y |
|
|
|
|
|
|
=γ |
α |
; |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
α |
|
0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
−2y |
+ y |
|
|
|
|
|
|
y |
|
|
− y |
|
|
|
|
|
||||||||||
y |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
i |
|
|
i |
|
|
i−1 |
+pi |
|
i+1 |
|
|
i−1 |
+qi yi |
= Fi |
, i = 1, 2, …, n–1; |
||||||||||||||
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2h |
|
|
|
|
|
|
|
|||||
α |
b |
|
|
yn − yn−1 |
|
|
|
+β |
b |
y |
n |
|
|
|
|
|
|
=γ |
b |
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
После приведения подобных слагаемых получаем: |
|||||||||||||||||||||||||||||||
(β h −α |
α |
) y |
+α |
|
y |
|
|
|
|
|
|
|
|
|
|
|
= γ |
α |
h ; |
||||||||||||
|
|
α |
|
|
0 |
|
|
α |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(2 |
− pih) yi−1 |
+(2h2qi − 4) yi |
+(2 + pih) yi+1 |
|
= 2h2Fi ; (5.14) |
||||||||||||||||||||||||||
−α |
b |
y |
n−1 |
|
|
|
|
+(β |
b |
h +α |
b |
) y |
n |
|
|
|
|
= γ |
b |
h . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Для краткости дальнейшего изложения введем обозначе-
ния
86

|
|
b0 = βah −αa ; |
c0 =αa ; |
f0 =γah; |
||||
a = 2 |
− p h; |
b = 2h2q −4; |
c = 2 |
+ p h; |
f |
i |
= 2h2F ; (5.15) |
|
i |
i |
i |
i |
i |
i |
|
i |
|
an = −αb ; |
bn = βbh +αb ; |
|
|
fn =γbh , |
||||
где i меняется от 1 до n–1.
С учетом (5.15) систему (5.14) можно переписать в стандартном виде:
|
|
|
|
|
|
b0 y0 |
|
+ c0 y1 |
|
= f0 , |
|
|||||||
a y |
|
|
+ b y |
|
|
+ c y |
2 |
|
|
= f |
, |
|
||||||
|
1 |
0 |
|
|
|
1 |
1 |
|
|
|
1 |
|
|
|
1 |
|
||
|
|
|
|
|
+ |
b2 y2 |
|
+ |
c2 y3 |
|
= |
f2 , |
(5.16) |
|||||
a2 y1 |
|
|
|
|||||||||||||||
… |
|
|
|
… … |
|
|
|
… … |
|
|
|
… … |
|
|||||
a |
|
y |
n−2 |
+ |
b |
|
y |
n−1 |
+ |
c |
|
y |
n |
= |
f |
n−1 |
, |
|
|
n−1 |
|
|
n−1 |
|
|
n−1 |
|
|
|
|
|||||||
an yn−1 |
+ bn yn |
|
|
|
|
|
|
= fn. |
|
|||||||||
Эту систему можно решить, используя метод Гаусса, трудоем-
кость которого ≈ 23 n3 арифметических операций. Однако нетруд-
но заметить, что матрица системы (5.16) является редкозаполненной, а именно трехдиагональной. В этой матрице все элементы, кроме элементов стоящих на главной диагонали (b0, b1, …, bn) и элементов, стоящих на диагоналях ниже (a0, a1, …, an) и выше (c0, c1, …, cn) главной диагонали, равны нулю. Поэтому, вопервых, в памяти ЭВМ имеет смысл хранить только эти три одномерных массива. Во-вторых, необходимо разработать метод, учитывающий упрощенную структуру матрицы системы (5.16).
Легко доказать, что решение системы (5.16) существует и является устойчивым при уменьшении шага сетки h. При малом значении h диагональные элементы системы (5.16) являются преобладающими. Т.е. | bi |>| ai | и | bi |>| ci |. Поэтому данная система имеет решение для любых непрерывных на отрезке [a, b], функ-
ций p(x), q(x) и F(x) .
Теперь разработаем алгоритм решения системы (5.10), учитывающий структуру системы. Для этого перепишем первые n
уравнений системы (5.16) в виде |
|
yi = Li yi+1 + Ki , i= 0, 1, …,n–1. |
(5.17) |
87
Из первого уравнения (5.16) получаем y = − |
c0 |
y + |
f0 |
. Следо- |
||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
b0 |
1 |
b0 |
|
|
вательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
L |
= − |
c0 |
; |
|
K |
0 |
= |
|
f0 |
. |
|
|
|
|
|
|
|
(5.18) |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
0 |
|
|
|
b0 |
|
|
|
|
|
b0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Получаем, |
|
|
y0 = L0 y1 + K0. |
|
|
|
|
|||||||||||||||
Подставим это выражение во второе уравнение системы (5.16). |
||||||||||||||||||||||
a1(L0 y1 + K0 ) +b1y1 +c1y2 = f1. Выражаем отсюда y1 |
|
|
||||||||||||||||||||
y |
= |
|
|
−c1 |
|
|
y |
|
+ |
f1 −a1K0 |
|
. Следовательно, |
|
|
|
|
||||||
a L +b |
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
|
|
|
2 |
|
|
a L |
+b |
|
|
|
|
|
|
|||||||
|
|
1 |
0 |
|
1 |
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
||||
L = |
−c1 |
|
|
|
; |
|
|
K |
= |
f1 −a1K0 |
. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
a1L0 |
+b1 |
|
1 |
a1L0 |
+b1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Поскольку все внутренние уравнения системы (5.16) имеют одинаковый вид, формулы для коэффициентов Li и Ki будут иметь такой же вид, как и для второго уравнения.
L = |
−ci |
; K |
i |
= |
fi −ai Ki−1 |
; i=1, 2, …, n. |
(5.19) |
|
|
|
|||||||
i |
ai Li−1 +bi |
|
|
ai Li−1 |
+bi |
|
|
|
|
|
|
|
|
|
|||
Коэффициенты Li и Ki являются рекуррентными, т.е., зная коэффициенты для предыдущего (i–1-го) уравнения, по формулам (5.19) получаем значения для текущего (i-го) уравнения. Таким образом, по формулам (5.18), (5.19) можно получить все коэффициенты Li и Ki. Массивы Li и Ki называются прогоночными коэффициентами, а шаг алгоритма, вычисляющий эти коэффициенты, называется прямым ходом метода прогонки. Получим теперь значение решения в правой граничной точке yn. Для этого выпишем последние два уравнения полученной системы:
y |
n−1 |
= |
L |
y |
n |
+ K |
n−1 |
, |
|
|
n−1 |
|
|
|
|||
an yn−1 +bn yn |
= |
fn . |
|
|
|
|
|
|
Исключая из |
этой |
системы неизвестную yn–1, получаем: |
||||||||||||
a L |
y |
n |
+ a K |
n−1 |
+b y |
n |
= f |
n |
. Отсюда |
y |
n |
= |
fn −an Kn−1 |
. Правая |
|
||||||||||||||
n n−1 |
|
n |
n |
|
|
|
|
bn + anLn−1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
часть этого выражения |
равна прогоночному коэффициенту Kn. |
|||||||||||||
Таким образом, решение в правой граничной точке выражается формулой:
yn = Kn . |
(5.20) |
88

Теперь, зная все прогоночные коэффициенты и решение yn, по рекуррентным формулам (5.17) можно последовательно получить решение во всех узловых точках сетки, начиная с yn–1 и до y1. Эта часть алгоритма называется обратным ходом метода.
Предложенный метод решения системы (5.16) имеет название
методом прогонки.
Приведем краткий алгоритм решения системы (5.14) методом прогонки.
1)Вычисление массивов ai, bi, ci и fi по формулам (5.15).
Прямой ход метода прогонки.
2)i=0. Вычисление прогоночных коэффициентов L0 и K0 по формулам (5.18).
3)i=i+1. Вычисление прогоночных коэффициентов Li и Ki по формулам (5.19).
4)Если i<n, то перейти на шаг 2.
Обратный ход метода прогонки.
5)yn=Kn.
6)i=i–1. Вычислить yi по формуле (5.16).
7)Если i>0, то перейти на шаг 6.
8)Конец подпрограммы.
Оценим трудоемкость метода прогонки.
На прямом ходе метода прогонки вычисляются прогоночные коэффициенты по формулам (5.18), (5.19). С учетом того, что коэффициенты имеют общий знаменатель, для их вычисления необходимо 6n арифметических операций. На обратном ходе необходимо выполнить еще 2n арифметических операций. Итого, трудоемкость метода прогонки равна 8n. Таким образом, метод
прогонки в ≈ n2 раз быстрее, чем метод Гаусса.
12
Вычислительная программа на Mathcad
Приведем программу, реализующую алгоритм метода прогонки. Для проверки работоспособности разработанной программы решим следующую тестовую краевую задачу, имеющую анали-
y′′− |
4y′+ 4y = e2x , 0 ≤ x ≤1, |
|
|
′ |
=1, |
тическое решение y(0) |
+ y (0) |
|
|
= 2e2. |
|
y′(1) |
|
|
89
Уравнение является линейным неоднородным уравнением второго порядка с постоянными коэффициентами. Решение по-
|
|
1 |
|
2 |
|
2 |
|
3 |
|
2 x |
|
ставленной задачи можно легко получить: |
y = |
|
x |
|
− |
|
x + |
|
e |
|
. |
2 |
|
7 |
7 |
|
|||||||
|
|
|
|
|
|
|
|
|
|||
В данной задаче p(x) = −4, q(x) = 4, F(x) = e2x , |
αa =1, |
βa =1, |
|||||||||
αb =1, βb = 0, γa =1, γb = 2e2. |
|
|
|
|
|
|
|
|
|
|
|
Приведем программу с достаточным числом комментариев, заключенных в прямоугольные блоки. При написании программы комментарии можно пропустить.
Начало программы.
Коэффициенты, задающие краевые граничные условия.
αa :=1 αb :=1 βa :=1 βb := 0 γa :=1 γb := 2 e2
Функции, задающие уравнение y′′+ p(x) y′+ q(x) y = F(x) .
F(x) := e2 x p(x) := −4 q(x) := 4
Параметры сетки. a := 0 b :=1 n :=10 h := b −n a
Ранжированные вектора, используемые для организации циклов.
i := 0..n j :=1..n k := n −1..0
Вычисление вектора узловых координат xi := a + h i
Вычисление векторов a, b, c и f, являющихся коэффициентами системы линейных алгебраических уравнений (5.16).
a := 2 − p(x ) h |
b := 2 h2 q(x ) −4 |
c := 2 + p(x ) h |
|||||
|
i |
|
i |
i |
i |
i |
i |
f |
i |
:= 2 h2 F(x ) |
b := βa h −αa |
c := |
αa |
||
|
|
i |
0 |
|
0 |
|
|
f0 :=γa h |
an := −αb |
bn := βb h +αb |
fn :=γb h |
||||
Вычисление прогоночных коэффициентов. (Прямой ход метода прогонки.)
L := −c0 |
K |
0 |
:= |
f0 |
|
|
|
|
||
|
|
|
|
|||||||
0 |
b0 |
|
|
b0 |
|
|
|
|||
|
|
|
|
|
|
|
||||
Lj := |
−c j |
|
|
K j := |
f j −a j K j−1 |
|
||||
a j Lj−1 |
+bj |
a j Lj−1 |
+bj |
|||||||
|
|
|
|
|||||||
Обратный ход метода прогонки.
yn := Kn |
yk := Lk yk +1 + Kk |
Теоретическое решение.
90
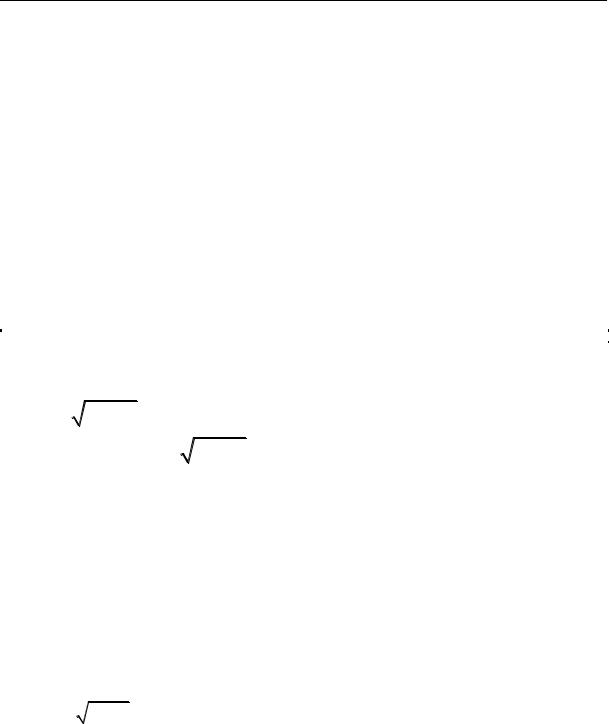
|
|
2 |
|
2 |
|
3 |
|
|
2 t |
yt(t) := |
0.5 t |
|
− |
|
t + |
|
|
e |
|
|
7 |
7 |
|
||||||
|
|
|
|
|
|
|
|
Конец программы.
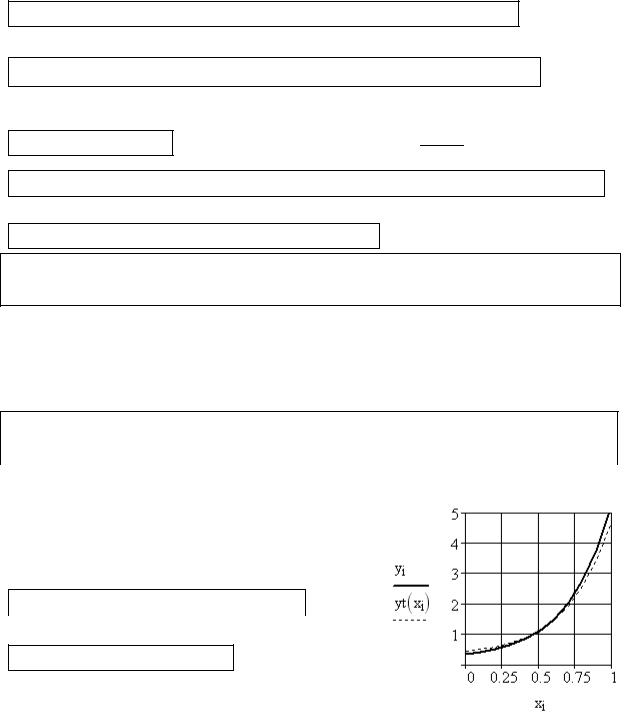
Для сравнения результатов, полученных по программе с теоретическими результатами, построим графики аналитического и численного решений. Численное решение получено при достаточно грубой сетке N=10. Следует отметить, что уже при N=40 графики совпадают. При решении практических задач необходимо удваивать значение параметра N до тех пор, пока не выполнится условие
max | y2iN − yiN / 2 |<ε , где ε – точность решения.
0≤i ≤N / 2
Задание для самостоятельной работы
|
|
|
|
|
′ ′′ |
|
|
Методом прогонки решить краевую задачу F(x, y, y , y ) = 0, |
|||||
на области x [a,b] с заданными граничными условиями. |
||||||
№ |
Дифференциальное уравнение |
[a, b] |
x=a |
x=b |
||
|
|
|
|
|
||
1 |
y′′+ln x y′+sin x y = xtg0,2x |
[1; 4] |
y′+3y =1 |
y′+ y = 0 |
||
2 |
y′′+ |
x2 + 2 y′+ 2−x y = sin2 x |
[–1; 2] |
y′ =1 |
y =1 |
|
3 |
y′′+(5x −1) y′− 3 x4 + 4 y = x4 |
[1; 5] |
y′+3y = 0 |
y′ = −2 |
||
4 |
y′′+3cos2 x y′−4x y = x4 sin x |
[–3; 3] |
y′ =1 |
y′+ y = 5 |
||
5 |
y′′− xtg0,5x y′+ x4 y = x |
[0; 2] |
y′+ 2y = 0 |
y = 5 |
||
6 |
y′′−3x y′+(2x2 +1) y = xex |
[–2; 2] |
y′−2y = 20 |
y′ =1 |
||
7 |
y′′+ctg2 0.5x y′− x4 y = xlg x |
[1; 2] |
y′+5y =100 |
y =100 |
||
8 |
y′′−lg2 (4x2 +3) y′+ xsin2 x y = x2 |
[0; 4] |
y =10 |
y =100 |
||
9 |
y′′+arcsin 0,1x y′- y arccos0,2x = x2 |
[–2;2] |
y′+5y =100 |
y′ =10 |
||
10 |
y′′−log4 (x2 +3) y′+ x2 y = 4x |
[–2; 2] |
y′+ y = −10 |
y′ =10 |
||
11 |
y′′+ x 5 |
x3 +1 y′−30,5x y = ex |
[–1; 8] |
y = 0 |
y′ = −100 |
|
12 |
y′′+ 2x y′−lg(x2 +1) y = e2x |
[0; 3] |
y′+ y = 0 |
y = 0 |
||
13 |
y′′−arcsin(0,1x) y′− y = 2x2 |
[–2; 3] |
y′+ y = −2 |
y =10 |
||
14 |
y′′−log2 (x2 + 4) y′+ 2x y = x2 |
[–1; 4] |
y′+ 2y = 0 |
y′+ 4y =1 |
||
15 |
y′′+ (3x2 + 4) y′+ e2x y = 2cos2 x |
[0; 2] |
y′ = −10 |
y′+ y =10 |
||
|
|
|
|
|
91 |
|
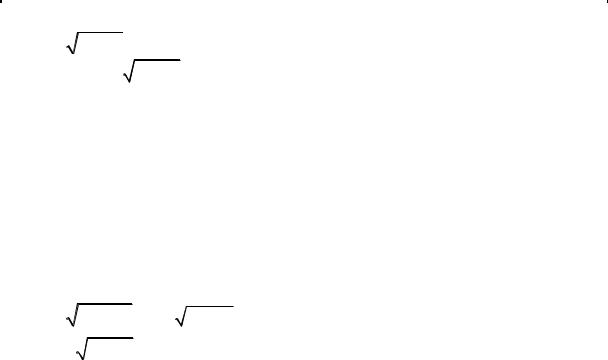
|
|
|
|
|
|
|
|
|
||||
16 |
y′′+ lg x y′+sin2 x y = x2tg0,1x |
|
|
[1; 4] |
y′+ 2y =1 |
y′+ y =1 |
||||||
17 |
y′′+ 4 |
|
|
|
y′+30,1x y = cos4 x |
|
|
[–1; 2] |
y′ = −10 |
y = −3 |
||
x2 + 2 |
|
|
||||||||||
18 |
y′′+5x2 y′− 3 x4 + 4 y = lg2 x |
|
|
[1;10] |
y = −10 |
y′+ y = 2 |
||||||
19 |
y′′− x2tg(0,5x) y′−(x4 + x) y = x4 |
|
[0; 2] |
y =10 |
y′+ y = 9 |
|||||||
20 |
y′′+ xlog2 (x2 +3) y′− 4x3 y = x |
|
|
[–1; 3] |
y =1 |
y =1 |
||||||
21 |
y′′− x30,5x y′+ 4x y = x4 +sin2 x |
|
|
[–3; 4] |
y′−3y =1 |
y′+ y = 0 |
||||||
22 |
y′′+ log2 (x2 | cos x | +1) y′+ x4 y =1 |
[–2; 2] |
y =10 |
y′ = −10 |
||||||||
23 |
y′′−lg2 (5x2 +1) y′+ x2 sin2 x y = x4 |
[1; 4] |
y = 2 |
y′ = −2 |
||||||||
24 |
y′′+ arcsin2 (0,2x2 ) y′−0,1x2 y = x |
|
[–2; 2] |
y′+ 4y =1 |
y′ = −2 |
|||||||
25 |
y′′−log5 (x2 + 4) y′+ x2 y =3 + 2x |
|
|
[–1; 3] |
y′+ 2y = 2 |
y′ = −10 |
||||||
26 |
y′′+ 3 3x2 + 4 y′+ |
4x + 6 y = x2 |
|
|
[–1; 3] |
y = −1 |
y = −2 |
|||||
27 |
y′′+ x 4 |
x2 + 7 y′+ ln(x2 + 7) y = x2 |
|
[2; 3] |
y′+3y = 3 |
y′+ 2y =1 |
||||||
28 |
y′′− x4 y′+ 2x y = lg2 (x2 + 2x +7) |
|
[–2; 4] |
y =10 |
y′ = −2 |
|||||||
29 |
′′ |
2 |
|
|
′ |
x |
2 |
|
[0; 4] |
y′+ 2 y = −1 |
y =0 |
|
|
|
1 ) y |
+ e y = 3 sin |
|
x |
|
|
|
||||
|
y +(3x + |
|
|
|
|
|
||||||
30 |
y′′ + (4x2 + 3) y′+ (2x + x) y = xex |
|
[–1; 2] |
y′ + 2 y = −1 |
y =10 |
|||||||
92
