24

6.4. Пуассоновский поток

Потоки случайных событий называются пуассоновскими, если число событий потока m, попадающих на любой участок , распределен по закону Пуассона

P_m=e^-a

где а – среднее число событий, находящихся на участке .

Пуассоновский поток является стационарным, если плотность событий  постоянна, тогда среднее число событий равно , иначе поток будет нестационарным.

Случайный поток событий, который обладает свойством стационарности, ординарности и не имеет последействия, называется простейшим и является стационарным пуассоновским потоком.

Просеянные потоки

Процесс переходов системы с дискретным временем функционирования может рассматриваться как воздействие дискретного потока событий, которое характеризуется тем, что в моменты времени t₁, t₂, ..., t_n события происходят с вероятностью P_i. Функция распределения такого потока:

Просеяние потока событий S₁, S₂, ... S_n, которые наступают в определенные моменты времени с вероятностями p₁, p₂, ... p_n, означает преобразование этих вероятностей в 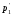, , ..., . Если поток является стационарным, то эти вероятности равны: ==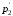...=1-. При этом  является константой просеивания, которая определяется либо воздействием какого-либо дестабилизирующего фактора, либо определяется исключением каких-либо событий из множества состояний системы.

Примерами потоков с ограниченным последействием являются потоки Эрланга. Они образуются закономерным просеиванием простейшего потока, при этом под закономерным просеиванием понимается процедура, в результате которой происходит исключение нескольких последующих событий в исходном потоке. Если у простейшего потока исключается каждое нечетное событие, то оставшиеся события образуют поток Эрланга II порядка. Промежуток времени между соседними событиями в таком потокепредставляет собой сумму независимых случайных величин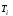и, распределенных по показательному закону (=+).

Если в простейшем потоке сохранить только каждое третье событие, то получим поток Эрланга III порядка и т.д. В общем случае, потоком Эрланга k-порядка называется простейший поток, полученный исключением (k-1) событий и сохранением k-го события.