2) Второе достаточное условие
Если функция g(x)
обладает второй производной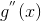 причем
в некоторой точке
причем
в некоторой точке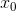 первая
производная равна нулю, а вторая
производная отлично от нуля. Тогда
точка
первая
производная равна нулю, а вторая
производная отлично от нуля. Тогда
точка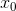 экстремум
функции g(x),
причем если
экстремум
функции g(x),
причем если 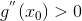 ,
то точка является максимумом; если
,
то точка является максимумом; если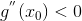 ,
то точка является минимумом.
,
то точка является минимумом.
3) Третье достаточное условие
Пусть
функция g(x) имеет в некоторой окрестности
точки 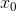 N
производных, причем значение первых (N
- 1)- ой и самой функции в этой точке равно
нулю, а значение N-ой производной отлично
от нуля. В таком случае:
N
производных, причем значение первых (N
- 1)- ой и самой функции в этой точке равно
нулю, а значение N-ой производной отлично
от нуля. В таком случае:
а)
Если N - четно, то точка 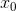 экстремум
функции:
экстремум
функции: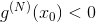 у
функции точка максимума,
у
функции точка максимума,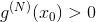 у
функции точка минимума.
у
функции точка минимума.
б)
Если N - нечетно, то в точке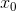 у
функции g(x) экстремума нет.
у
функции g(x) экстремума нет.
Абсолютный экстремум
Наибольшее(наименьшее)
значение на сегменте [a;b] непрерывной
функции g(x) достигается или в критической
точке этой функции(т.е. где производная
равна нулю или не существует), или в
граничных точках а и b данного сегмента

