Тема 25

134

25. Элементы математической теории оптимального управления

25.1. Постановка задачи оптимального управления экономической системой

В отличии от метода динамического программирования, в теории управления экономическими процессами управление осуществляется непрерывно.

Критерии оптимальности управления обычно связаны либо с получением наибольшей прибыли, либо с достижением минимальных экономических затрат, либо с обеспечением минимального времени процесса. Самым распространенным на практике является критерий минимальных экономических затрат.

Пусть исследуемый экономический процесс, подлежащий управлению, представляет собой перепрофилирование производства, организацию дополнительных цехов, предприятий и т.д. с целью увеличения выпуска продукции. Обозначим y(t) - объем выпускаемой продукции в единицу времени, который естественно будет изменяться во времени t при перепрофилировании производства.

Пусть далее функция u(t) характеризует управление экономическим процессом. Она может представлять собой текущие инвестиции в процесс перепрофилирования, количество рабочей силы, направляемой для этой цели в момент времени t, число единиц специальной техники и т.п. Ясно, что вид функции y(t) зависит от того, какой будет выбрана функция u(t).

Кроме того, очевидно, что в каждый момент времени t текущие экономические затраты g будут зависеть от вида функций y(t) и u(t), т.е.

g = g(y(t), u(t), t).

Чтобы найти полные экономические затраты нужно проинтегрировать g в пределах от момента начала исследуемого процесса t₀ до момента его окончания t_k. Тогда критерием оптимальности управления является минимизация интеграла

,

где управление u(t) принадлежит некоторому классу U возможных функций, а y(t) определяется начальным состоянием системы и видом управления, т.е. видом функции u(t).

Определенный интеграл в правой части равенства является числом, которое зависит от выбора функции u(t). Если каждой функции из некоторого множества функций поставлено в соответствие определенное число, то говорят, что задан функционал. В приведенном выше интеграле J(y(t), u(t)) является функционалом.

Как правило, скорость увеличения объема продукции при перепрофилировании производства является функцией вида управления и самого объема производства. То есть имеет место дифференциальное уравнение:

,

здесь производная по времени обозначена точкой.

Кроме того, естественно, известно состояние экономической системы (объем производства) в начальный момент:

y(t₀) = y₀

и задано состояние системы в конечный момент (т.е. объем производства, на который производство должно быть перепрофилировано в момент окончания процесса):

y(t_k) = y_k.

Таким образом математически задача оптимального управления экономической системой может быть поставлена следующим образом:

Требуется определить функции u(t) и y(t), минимизирующие функционал

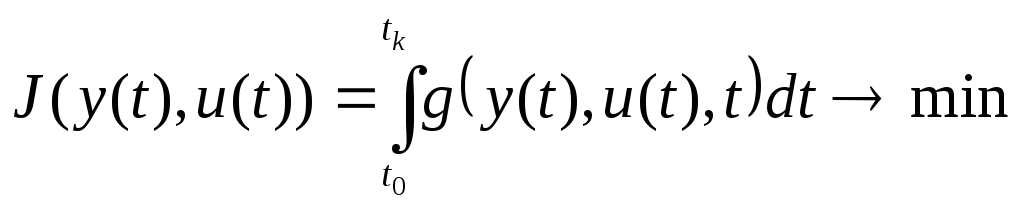
При этом y(t_k) = y_k , а функции y(t) и u(t) связаны дифференциальным уравнением с начальным условием y(t₀) = y₀. В этом случае функция u(t) называется оптимальным управлением и обозначается u^*(t), а y(t) называется функцией оптимальных параметров производства и обозначается y^*(t).

Следует отметить, что в литературе обычно рассматривается более общий случай, когда экономическая система характеризуется не одной переменной (в нашем случае объем производства), а несколькими. При этом управление также включает ряд управляющих параметров. В этом случае y и u представляют собой вектор-функции: y(t) = (y₁(t), y₂(t), … y_n(t)); u(t) = (u₁(t), u₂(t), … u_m(t)). Мы же рассматриваем простейший случай n = m = 1.

Поставленная выше задача называется задачей Лагранжа. Принцип оптимальности Лагранжа, согласно которому отыскивается вид оптимальной функции управления, является развитием задачи нахождения условного и безусловного экстремумов.

Рассмотрим алгоритм решения задачи Лагранжа.

1. Составляется функция Лагранжа. Очень часто эту функцию называют  - функционалом:

.

2. Составляется функция Гамильтона (гамильтониан) H, которая учитывает скорости изменения рассматриваемых функций:

,

где - неизвестная функция времени, которая называется неопределенным множителем.

Доказана следующая теорема: Пусть гамильтониан H(, y, u, t) дифференцируем по u, существует его экстремум в точке u^* и соответствующая функция y*(t) является оптимальной, т.е. дает экстремум гамильтониану H . Тогда можно найти такое оптимальное значение * и оптимальную функцию , что экстремум гамильтониана H совпадет с минимальным значением функционала J(y,u). Иначе говоря, у этих функционала и гамильтониана оптимальный вид функций y^*(t) и u^*(t) совпадает.

В соответствии с этой теоремой можно получить следующие необходимые условия экстремума:

и .

Решение системы из этих двух уравнений позволяет получить оптимальную функцию управления u^*(t). При этом по условиям задачи Лагранжа начальное условие для неизвестно. Обычно задается лишь конечное условие в виде

.

Пример. Задана некоторая система, процесс функционирования которой описывается дифференциальным уравнением

,

определяющим скорость изменения его основной характеристики y = y(t) в зависимости от управления u(t).

Известны начальное и конечное состояния системы: t₀ = 0; t_k=1; y(t₀) = 0, y(t_k) = 1. Найти оптимальное управление u^* и соответствующую ему функцию y^*, которые доставляют минимальное значение функционалу

Решение.

По условию задачи и g(y,u,t) = u² + y. Составим -функционал и гамильтониан:

;

.

Для вычисления неопределенного множителя (t) продифференцируем гамильтониан по u и приравняем к нулю. Имеем

.

Откуда

.

Далее

^,

откуда

.

Так как по конечному условию

,

то . Отсюда .

Таким образом, оптимальная зависимость неопределенного множителя ^*(t) будет иметь вид:

.

В последнем выражении неизвестным является ^*. Для его нахождения воспользуемся исходным дифференциальным уравнением . Подставляя в это уравнение

и интегрируя, получим

.

Воспользовавшись начальным условием y(0)=0, получим C₁=0.

Таким образом, имеем оптимальную функцию производства:

.

Подставляя в это выражение конечное условие y(1)=1, вычисляем . Окончательно, оптимальная функция будет иметь вид:

,

а оптимальная функция управления:

.

Минимальное значение функционала J(y, u) равно:

.

25.2. Принцип максимума Понтрягина

При решении задачи Лагранжа или задачи оптимального управления предполагалось, что управление носит неограниченный характер. На практике управление всегда ограничено по величине. Это ограничение связано с конечным значением возможностей управления.

Пусть ограничение на управление имеет вид, изображенный на рис.25.1.

По задаче Лагранжа

45⁰

- u_{max 0} +u_max u

Рис. 25.1. Реальный и идеальный случаи управления

Тогда в место управления u необходимо использовать, как показано на рис.25.1, нелинейную функцию , которая будет являться аргументом функционала Гамильтона. При такой нелинейности дифференцировать гамильтониан нельзя.

Впервые задачу Лагранжа с ограничением решила группа ученых под руководством академика Л.С. Понтрягина. Решение задачи явилось обобщением принципа Лагранжа.

Запишем формулировку задачи принципа максимума Понтрягина: дан объект управления, модель которого описывается дифференциальным уравнением

=.

Даны начальные условия y(t₀)=y₀ и заданы ограничения. Рассмотрим два ограничения

q₁ (y_k)= 0;

q₂ (y_k)= 0.

Аналогично даны ограничения по скорости изменения функций

= ;

= .

В отличие от предыдущей задачи добавляется еще ограничения на функцию управления

;

.

Необходимо определить оптимальный вид функций y^* и u^*, которые обеспечивают минимальное значение целевой функции I(y^*, u^*) при выполнении всех перечисленных выше ограничений. Т.е.

I(y,u)=.

При решении, аналогично задаче Лагранжа, составляются функционалы Лагранжа и Гамильтона:

= I(y, u)+ q₁[y_k]+ q₂[y_k],

H=+ - g(y,u).

Далее воспользуемся теоремой, которую называют принципом максимума Понтрягина:

Если при оптимальных функциях y^* и u^*существует минимальное значение целевой функции I(y^*, u^*) при выполнении всех перечисленных выше ограничений, то тогда можно найти такие оптимальные функции , , , , при которых функционал Гамильтона принимает максимальное значение, т.е.

.

Заметим, что в последнем выражении для нахождения управляющей функции u^* не производится дифференцирование гамильтониана, а ее значение отыскивается путем перебора.

Сделаем несколько замечаний:

1. Постановка задачи Понтрягина отличается от задачи Лагранжа тем, что включается дополнительное ограничение на управление.

2. Принцип максимума позволяет найти максимум функционалов на концах отрезка, как это изображено на рис. 25.2, т.к. он не требует дифференцирования гамильтониана.

H

- u_max 0 +u_max u

Рис.25.2. Вид функционала Гамильтона на отрезке

При этом, если управление u невелико и концентрируется на небольшом отрезке, не достигая границ ограничения, то принцип Понтрягина сводится к решению задачи Лагранжа. Если управление выходит на границу отрезка, то задача решается в постановке Понтрягина и максимум гамильтониана отыскивается путем простой подстановки.

Пример.

Дана система, описываемая уравнением

.

Известно начальное условие y(0)=0 и ограничение . Найти оптимальное управление и соответствующую ему функцию, которые доставляют минимальное значение целевой функции

I(y,u)=min.

Заметим, что в условии примера управляющая функция не входит в подынтегральную функцию. Кроме того, отсутствуют ограничения на конечное условие q и скорость изменения функции . Легко убедиться, что в этом случае функционал Лагранжа совпадает с целевой функцией I(y,u).

Решение. Приведем к постановке задачи Понтрягина. Для этого обозначим и запишем гамильтониан в виде

H=u - y.

Применим к последнему выражению принцип Понтрягина

(u - y) при ограничении.

Выражение в скобках состоит из двух слагаемых, из которых второе не зависит от u. Тогда

(u - y) = u при .

Следовательно, .

По определению

.

Интегрируя, получим

.

Для вычисления постоянной воспользуемся соотношением

,

но - функционал в условии задачи не зависит от y(t_k). Поэтому полагаем

=0.

Кроме того, по условию задачи t_k =4, тогда

.

Откуда C₁=-4. Следовательно

.

Построим эту функцию

0 4 t

-4

Рис.25.3. График функции неопределенного множителя

Из рис.25.3 видно, что на отрезке [0,4], на котором производится минимизация целевой функции I(y,u) , множитель . Так как , то . Подставив это значение в исходное дифференциальное уравнение, найдем . Интегрируя последнюю формулу, находим . С учетом начального условия получим .

Тогда

I()=.

При любом другом управлении меньшее значение получить нельзя.

Пример.

Найти оптимальное управление в системе, описываемой уравнением

.

Дано начальное условие y(0)=0 и ограничение . Найти оптимальное управление и соответствующую ему функцию, которые доставляют минимальное значение целевой функции

I(y,u)=min.

Решение. Так как ограничения на конечные значения отсутствуют, то

I(y,u).

Обозначим и составим гамильтониан

H=u - (u² + y).

Применим принцип Понтрягина

(u - y – u²) при ограничении.

Рассмотрим в начале интервал.

Необходимое условие экстремума дает

–2 u=0.

Откуда

при .

Для вычисления воспользуемся

.

Аналогично вычислениям в примере 2 получаем

.

Вид этой функции показан на рис.19.3 . Подставляя полученную функцию в выражение для u, получим

.

Но , тогда . Откуда 2 < t < 6.

По условию задачи правый конец интервала =4, поэтому принимаем

2 < t 4.

Теперь рассмотрим случай, когда . В соответствии с проведенными вычислениями и рис.19.3 этот случай может быть только на отрезке 0 t 2. Аналогично вычислениям в примере 2

.

Из рис.19.3 видно, что на отрезке [0,2], на котором производится минимизация целевой функции I(y,u) , множитель . Тогда .

Таким образом, управляющая функция будет иметь вид

Тогда, подставляя управляющую функцию в исходное уравнение, оптимальная система с точки зрения заданного критерия и ограничений будет описываться дифференциальным уравнением

На рис.25.4 показаны полученные функции.