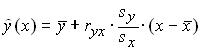эконометрика
.docxЕсли функция регрессии нелинейная, то оценка значимости ее параметров производится
-
для линеаризованной формы функции
Система
линейных алгебраических уравнений для
определения методом наименьших квадратов
значений параметров a.b
уравнения![]() по выборке объема n имеет вид:
по выборке объема n имеет вид:
По 25-ти
наблюдениям построено уравнение
регрессии![]() . Коэффициент линейной корреляции
составил 0,7. После включения в модель
фактора
. Коэффициент линейной корреляции
составил 0,7. После включения в модель
фактора![]() индекс множественной корреляции
составил 0,8. На уровне значимости 0,05
табличное значение F-критерия равно
4,3. Включение в эконометрическую модель
фактора
индекс множественной корреляции
составил 0,8. На уровне значимости 0,05
табличное значение F-критерия равно
4,3. Включение в эконометрическую модель
фактора
![]() значимо, так как фактическое значение
частного F-критерия равно
значимо, так как фактическое значение
частного F-критерия равно
-
9,2
По наблюдаемым значениям признака-результата Y и факторных признаков вычислены значения величин: Правильным является заключении
-
Можно рекомендовать исключить из модели фактор

Если число коэффициентов эконометрической структурной модели равно числу коэффициентов соответствующей приведенной модели и структурные коэффициенты однозначно определяются по приведенным коэффициентам, то структурная модель называется
-
Идентифицируемой
Проверка статистической гипотезы об отсутствии гетероскедастичности случайного члена в регрессионной модели по выборкам большого объема требует вычисления статистики по формуле:
При построении мультипликативной модели уровня временного ряда скорректированные значения сезонной компоненты вычисляют по формуле:
При построении аддитивной модели уровня временного ряда скорректированное значение сезонной компоненты вычисляют по формуле:
Результатом
преобразования уравнения![]() к линейному виду относительно параметров
регрессии является уравнение:
к линейному виду относительно параметров
регрессии является уравнение:
При построении
уравнения регрессии по наблюдаемым
значениям признаков X и
Y с применением метода
наименьших квадратов уравнение![]() следует преобразовать к виду:
следует преобразовать к виду:
Случайные колебания в динамике изучаемого показателя объясняются влиянием
-
второстепенных факторов на моделируемый уровень ряда
Общая вариация зависимой переменной связана с факторной (объясненной) суммой квадратов отклонений для регрессии и с остаточной суммой квадратов отклонений для регрессии
-
равенством:

Доля вариации уровней временного ряда, не объясняемая тенденцией, измеряется величиной
Если:
![]() , то стандартизованные коэффициенты
регрессии
, то стандартизованные коэффициенты
регрессии
![]() являются решением системы уравнений:
являются решением системы уравнений:
Совокупное и долговременное воздействие множества факторов на изменение изучаемого показателя может формировать
-
тенденцию в динамике показателя (тренд ряда)
Целесообразность включения факторов в модель регрессии можно оценить с помощью
-
коэффициентов частной корреляции
Корреляционная
зависимость между значениями случайных
остатков
![]() и
и
![]() при моделировании уровней показателя
временного ряда называется
при моделировании уровней показателя
временного ряда называется
-
автокорреляцией в остатках
Вычислены
частные коэффициенты линейной корреляции
первого порядка:
![]() Тогда частный коэффициент линейной
корреляции второго порядка
Тогда частный коэффициент линейной
корреляции второго порядка![]() равен
равен
-
0,24
По 27-ти наблюдениям за изменениями значений признаков X и Y значение парного коэффициента линейной корреляции составило 0,6. При проверке значимости степени тесноты линейной связи между признаками фактическое значение приемлемого статистического критерия составило
-
3,75
При проверке
нулевой гипотезы о несмещенности
случайных отклонений![]() в нелинейных моделях регрессии в
качестве статистического критерия
рассматривается статистика:
в нелинейных моделях регрессии в
качестве статистического критерия
рассматривается статистика:
Для
эконометрической модели, выраженной
системой уравнений в отклонениях
переменных от их средних![]() уровней , вычислены значения величин:
уровней , вычислены значения величин:
 Тогда приведенное уравнение регрессии
для эндогенной переменной имеет вид:
Тогда приведенное уравнение регрессии
для эндогенной переменной имеет вид:
Для
эконометрической модели, выраженной
системой уравнений
![]() ошибка
ошибка
![]() в уравнении для эндогенной переменной
в уравнении для эндогенной переменной![]() приведенной формы эконометрической
модели
приведенной формы эконометрической
модели
-
выражается формулой:

Матрица коэффициентов при эндогенных переменных в системе рекурсивных уравнений может иметь вид:
По наблюдаемым значениям признака-результата Y и факторных признаков вычислены значения величин: Правильным является заключение:
-
Факторы взаимосвязаны
Если коэффициент парной линейной корреляции равен 0.6, то коэффициент парной линейной детерминации для тех же данных равен
-
0,36
Пусть:
![]() уравнение регрессии и выборочные
дисперсии значений признаков X и Y
соответственно. Тогда выборочный
коэффициент парной линейной корреляции
равен
уравнение регрессии и выборочные
дисперсии значений признаков X и Y
соответственно. Тогда выборочный
коэффициент парной линейной корреляции
равен
-
0,36
Критерий Дарбина-Уотсона (DW) и коэффициент автокорреляции остатков связаны равенством:
Для данного
временного ряда вычислены значения
величин:
![]() Коэффициент автокорреляции второго
порядка равен
Коэффициент автокорреляции второго
порядка равен
-
0,80
Система
четырех одновременных эконометрических
уравнений включает m
экзогенных переменных. Необходимое
условие точной идентифицируемости
уравнения
![]() выполняется при
выполняется при
Система
линейных алгебраических уравнений для
определения методом наименьших квадратов
значений параметров a,b
уравнения![]() по выборке объема n имеет
вид:
по выборке объема n имеет
вид:
Для сопоставления факторов по силе влияния на изменение признака-результата можно пользоваться
-
стандартизованными коэффициентами регрессии
Если остатки![]() и объясняющая (независимая) переменная
не коррелированны, то:
и объясняющая (независимая) переменная
не коррелированны, то:
Пусть:
![]() уравнение регрессии и выборочные
дисперсии значений признаков X
и Y соответственно. Тогда
выборочный коэффициент парной линейной
корреляции равен
уравнение регрессии и выборочные
дисперсии значений признаков X
и Y соответственно. Тогда
выборочный коэффициент парной линейной
корреляции равен
-
0,36
Исследование нелинейных моделей регрессии на несмещенность случайных отклонений сводится к проверке статистической гипотезы
По 25-ти
наблюдениям построено уравнение
регрессии![]() . Индекс множественной корреляции
составил 0,7. На уровне значимости 0,05
табличное значение F-критерия равно
3,35. Построенная регрессионная модель
значима, так как фактическое значение
F-критерия равно
. Индекс множественной корреляции
составил 0,7. На уровне значимости 0,05
табличное значение F-критерия равно
3,35. Построенная регрессионная модель
значима, так как фактическое значение
F-критерия равно
-
10,57
Если:
![]() , то стандартизованные коэффициенты
регрессии
, то стандартизованные коэффициенты
регрессии![]() являются решением системы уравнений:
являются решением системы уравнений:
Регрессией, нелинейной относительно оцениваемых параметров, является уравнение
Для оценки значимости уравнения множественной регрессии используют
-
общий F-критерий (критерий Фишера)
Долю вариации зависимой переменной, объясненную вариацией факторов, включенных в модель множественной регрессии, характеризует
-
индекс детерминации
Для проверки значимости выборочного коэффициента парной линейной корреляции используют критерий
-
Стьюдента
По данным, характеризующим некоторый объект за несколько последовательных моментов или периодов времени, можно построить
-
модели временного (динамического) ряда
Расчету оценки сезонной компоненты в модели уровня временного ряда предшествует
-
сглаживание ряда методом четырехчленной скользящей средней
В уравнении
регрессии![]() величины a,b являются
величины a,b являются
-
параметрами уравнения регрессии
Для
эконометрической модели, выраженной
системой уравнений в отклонениях
переменных от их средних уровней![]() , вычислены значения величин:
, вычислены значения величин:
 Тогда приведенное уравнение регрессии
для эндогенной переменной
Тогда приведенное уравнение регрессии
для эндогенной переменной![]() имеет вид:
имеет вид:
Приведенная форма некоторой структурной модели может быть выражена системой уравнений:
За последовательные 4 года по каждому кварталу вычислены суммы значений оценки сезонной компоненты:

Скорректированные значения сезонной компоненты равны соответственно:
При использовании ступенчатого регрессионного анализа при выборе наилучшей эконометрической регрессионной модели повторяется процедура определения зависимости случайных остатков текущей модели
-
от фактора, следующего по убыванию степени влияния на признак-результат
При
моделировании тенденции в динамике
показателя уравнением![]() вычислены значения величин:
вычислены значения величин:
 Тогда оценки параметров тренда
Тогда оценки параметров тренда
-
можно определить из равенств: ln a = 4,2; ln b = – 0,4
Исследование стабильности (постоянства) дисперсии случайных отклонений в моделях регрессии сводится к проверке статистической гипотезы о равенстве
-
двух дисперсий случайных отклонений в модели регрессии
Результатом преобразования уравнения
 к линейному виду относительно параметров
регрессии является уравнение:
к линейному виду относительно параметров
регрессии является уравнение:
Если:
![]() , то значение выборочного коэффициента
парной линейной корреляции (с точностью
0,01) равно
, то значение выборочного коэффициента
парной линейной корреляции (с точностью
0,01) равно
-
– 0,99
Для эконометрической модели, выраженной
системой уравнений
![]() свободный член уравнения регрессии
для
свободный член уравнения регрессии
для![]() приведенной формы эконометрической
модели
приведенной формы эконометрической
модели
-
выражается формулой:

Матрица коэффициентов при экзогенных переменных приведенной формы эконометрической модели может иметь вид:
Автокорреляция уровней временного ряда – это корреляционная связь между последовательными значениями
-
уровней ряда
Если значение выборочного коэффициента парной линейной корреляции близко к нулю, то можно предположить, что
-
существует тесная нелинейная корреляционная связь между признаком-результатом и факторным признаком
Для эконометрической модели, выраженной
системой уравнений в отклонениях
переменных от их средних уровней![]() , вычислены значения величин:
, вычислены значения величин:
 Тогда приведенное уравнение регрессии
для эндогенной переменной имеет вид:
Тогда приведенное уравнение регрессии
для эндогенной переменной имеет вид:
За последовательные 4 года по каждому
кварталу вычислены суммы значений
оценки сезонной компоненты:
 Скорректированные значения сезонной
компоненты равны соответственно:
Скорректированные значения сезонной
компоненты равны соответственно:
Пусть: Y – признак-результат;
![]() –признаки - факторы. По исходным данным
вычислены средние уровни признаков,
средние квадратические отклонения
значений признаков от средних уровней
признаков
–признаки - факторы. По исходным данным
вычислены средние уровни признаков,
средние квадратические отклонения
значений признаков от средних уровней
признаков
![]() и построено уравнение регрессии в
стандартизованном масштабе
и построено уравнение регрессии в
стандартизованном масштабе
![]() .
Тогда теоретические (расчетные) значения
признака-результата вычисляют по
формуле:
.
Тогда теоретические (расчетные) значения
признака-результата вычисляют по
формуле:
Уравнение![]() , отражающее корреляционную связь между
признаком-результатом Y и признаками-факторами
, отражающее корреляционную связь между
признаком-результатом Y и признаками-факторами![]() , это –
, это –
-
множественная регрессия
Если![]()
![]()
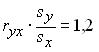 , то параметр a в уравнении парной
линейной регрессии
, то параметр a в уравнении парной
линейной регрессии
![]() равен
равен
-
0,6
Вычислены частные коэффициенты линейной
корреляции первого порядка:
![]() Тогда частный коэффициент линейной
корреляции второго порядка
Тогда частный коэффициент линейной
корреляции второго порядка
![]() равен
равен
-
0,48
Уравнение парной линейной регрессии имеет вид:
Метод наименьших квадратов позволяет получить такие оценки параметров уравнения регрессии, при которых
-
сумма квадратов отклонений наблюдаемых значений признака-результата от теоретических (расчетных) минимальна
По 30-ти наблюдениям построено уравнение
регрессии![]() и вычислены фактические значения
t-критерия:
и вычислены фактические значения
t-критерия:
![]() .
На уровне значимости 0,05 табличное
значение t-критерия равно 2,05. Тогда
доверительный интервал для параметра
.
На уровне значимости 0,05 табличное
значение t-критерия равно 2,05. Тогда
доверительный интервал для параметра
![]() (при
(при
![]() )
функции регрессии:
)
функции регрессии:
-
(0.635 , 1.045)
Если критическое (табличное) значение F–критерия (критерия Фишера) равно числу 6.12, то нулевая гипотеза о статистической незначимости уравнения регрессии отклоняется в пользу конкурирующей гипотезы при условии:
Наиболее вероятно, что временной ряд характеризуется наличием тенденции в динамике изучаемого показателя при следующих значениях коэффициентов автокорреляции:
По 30-ти наблюдениям построено уравнение
регрессии
![]() и вычислены фактические значения
t-критерия:
и вычислены фактические значения
t-критерия:
![]() . На уровне значимости 0,05 табличное
значение t-критерия равно 2,05. Тогда
доверительный интервал для параметра
. На уровне значимости 0,05 табличное
значение t-критерия равно 2,05. Тогда
доверительный интервал для параметра
![]() (при
(при![]() ) функции регрессии:
) функции регрессии:
-
(– 3.82 , – 0.38)
Для сопоставления факторов по силе влияния на изменение признака-результата можно пользоваться
-
коэффициентами эластичности
При проверке нулевой гипотезы о
несмещенности случайных отклонений![]() в нелинейных моделях регрессии в
качестве статистического критерия
рассматривается статистика:
в нелинейных моделях регрессии в
качестве статистического критерия
рассматривается статистика:
Косвенный метод наименьших квадратов применим к вычислению структурных коэффициентов систем одновременных уравнений, выражающих
-
точно идентифицируемые эконометрические модели
Средние значения оценки периодической
компоненты для данного временного ряда
составили:
![]() Скорректированные значения периодической
компоненты равны соответственно:
Скорректированные значения периодической
компоненты равны соответственно:
Система шести одновременных эконометрических
уравнений включает m экзогенных
переменных. Условие неидентифицируемости
уравнения![]() выполняется при
выполняется при
В уравнении регрессии
![]() величины a,b являются
величины a,b являются
-
параметрами уравнения регрессии
Если наблюдается непрерывный рост уровней показателя со снижающимися темпами роста, то модель тенденции в динамике показателя можно выразить уравнением:
Факторная (объясненная) сумма квадратов отклонений для регрессии вычисляется по формуле:
В множественной регрессии показателями тесноты корреляционной связи являются
-
индексы множественной корреляции и детерминации
По 14-ти наблюдениям построено уравнение
регрессии
![]() и вычислены значения сумм квадратов
отклонений:
и вычислены значения сумм квадратов
отклонений:
![]() На уровне значимости 0,05 табличное
значение F-критерия равно 3,98. Построенная
регрессионная модель незначима, так
как фактическое значение F-критерия
равно
На уровне значимости 0,05 табличное
значение F-критерия равно 3,98. Построенная
регрессионная модель незначима, так
как фактическое значение F-критерия
равно
-
3,85
Матрица коэффициентов при эндогенных переменных приведенной формы эконометрической модели может иметь вид:
За последовательные 3 года по каждому
кварталу вычислены суммы значений
оценки сезонной компоненты:
 Корректирующий показатель для определения
значений сезонной компоненты равен
Корректирующий показатель для определения
значений сезонной компоненты равен
-
0,0900
Наиболее вероятно, что временной ряд характеризуется наличием периодических колебаний в динамике изучаемого показателя при следующих значениях коэффициентов автокорреляции:
По последовательности коэффициентов автокорреляции уровней временного ряда и соответствующим значениям лага строят
-
Коррелограмму
Пусть: Y – признак-результат;
![]() –признаки - факторы. По исходным данным
вычислены средние уровни признаков и
средние квадратические отклонения
значений признаков от средних уровней
признаков:
–признаки - факторы. По исходным данным
вычислены средние уровни признаков и
средние квадратические отклонения
значений признаков от средних уровней
признаков:
![]() Преобразование уравнения “чистой”
регрессии (уравнения регрессии в
натуральном масштабе) к уравнению
регрессии в стандартизованном масштабе
выполняют по формулам:
Преобразование уравнения “чистой”
регрессии (уравнения регрессии в
натуральном масштабе) к уравнению
регрессии в стандартизованном масштабе
выполняют по формулам:
Если: n – объем выборки,
![]() , – наблюдаемые значения признака-результата
Y и факторного признака X соответственно,
то параметры a,b уравнения парной линейной
регрессии
, – наблюдаемые значения признака-результата
Y и факторного признака X соответственно,
то параметры a,b уравнения парной линейной
регрессии![]() , можно определить как решение системы
уравнений:
, можно определить как решение системы
уравнений:
Система линейных алгебраических
уравнений для определения методом
наименьших квадратов значений параметров
a,b уравнения
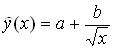 по выборке объема n имеет вид:
по выборке объема n имеет вид:
За
последовательные 4 года по каждому
кварталу вычислены суммы значений
оценки сезонной компоненты:
 Скорректированные значения сезонной
компоненты равны соответственно:
Скорректированные значения сезонной
компоненты равны соответственно:
Если:
![]() , то стандартизованные коэффициенты
регрессии
, то стандартизованные коэффициенты
регрессии![]() являются решением системы уравнений:
являются решением системы уравнений:
-
 \
\
Для оценки структурных параметров сверхидентифицируемых эконометрических моделей, выраженных системами одновременных уравнений, можно пользоваться
-
двухшаговым методом наименьших квадратов
Оценивание качества уравнения регрессии состоит
-
в проверке нулевой гипотезы о статистической незначимости индекса детерминации
Для нелинейной модели с помощью МНК
построено уравнение регрессии и вычислены
значения величин:
 Табличное значение приемлемого
статистического критерия равно 2,1.
Следовательно, нет оснований отклонять
предположение
Табличное значение приемлемого
статистического критерия равно 2,1.
Следовательно, нет оснований отклонять
предположение
-
несмещенности случайного отклонения в модели регрессии
Коэффициент парной линейной корреляции
-
характеризует степень тесноты линейной корреляционной связи между признаком-результатом и факторным признаком
Фактическое значение критерия Стьюдента
(t-критерия) для параметра![]() множественной линейной регрессии,
вычисленного со стандартной ошибкой
множественной линейной регрессии,
вычисленного со стандартной ошибкой![]() ,
вычисляют по формуле:
,
вычисляют по формуле:
Если вычислены значения величин:
![]() по данным значениям признака-результата
Y и факторного признака X , то уравнение
парной линейной регрессии можно составить
по правилу, выраженному равенством:
по данным значениям признака-результата
Y и факторного признака X , то уравнение
парной линейной регрессии можно составить
по правилу, выраженному равенством:
Вычислены частные коэффициенты линейной
корреляции первого порядка:
![]() Тогда частный коэффициент линейной
корреляции второго порядка
Тогда частный коэффициент линейной
корреляции второго порядка![]() равен
равен
-
0,38
Если наблюдаются стабильные темпы роста показателя, то модель тенденции в динамике показателя можно выразить уравнением:
В уравнение множественной регрессии должны быть включены факторы, которые
-
тесно связаны корреляционной зависимостью с признаком-результатом и слабо между собой
Вычислены частные коэффициенты линейной
корреляции первого порядка:
![]() Тогда частный коэффициент линейной
корреляции второго порядка
Тогда частный коэффициент линейной
корреляции второго порядка![]() равен
равен
-
0,29
Для линейной регрессионной модели с
помощью МНК построено уравнение регрессии
и вычислено значение величины:
 Табличное значение критерия Стьюдента
на уровне значимости 0,05 равно 2,01.
Следовательно, отклоняется предположение
об отсутствии
Табличное значение критерия Стьюдента
на уровне значимости 0,05 равно 2,01.
Следовательно, отклоняется предположение
об отсутствии
-
гетероскедастичности случайного члена регрессии
За последовательные 3 года по каждому
кварталу вычислены суммы значений
оценки сезонной компоненты:
 Корректирующий показатель для определения
значений сезонной компоненты равен
Корректирующий показатель для определения
значений сезонной компоненты равен
-
0,0900
Для эконометрической модели, выраженной
системой уравнений в отклонениях
переменных от их средних уровней![]() , вычислены значения величин:
, вычислены значения величин:
 Тогда приведенное уравнение регрессии
для эндогенной переменной имеет вид:
Тогда приведенное уравнение регрессии
для эндогенной переменной имеет вид: