
множество
.docx
понятие о множестве и его свойства
Множество
Множество – это совокупность элементов, которые воспринимаются как единое целое. Множество состоит из элементов. Множество ассоциируется с понятием группа. Чем больше элементов во множестве, тем множество мощнее. В детском саду множества могут быть конечными, бесконечными, пустыми и состоять из пяти элементов.
-
Конечные множества – это такие элементы, которые можно посчитать;
-
Бесконечное множество – это такое множество, в которых элементы посчитать невозможно (натуральный ряд чисел, звезды, песчинки…);
-
Дискретные или непрерывные множества – это такое множество в которых каждый элемент можно воспринимать отдельно;
-
Непрерывные множества – когда элементы отдельно не воспринимаются (длина стола, стакан воды);
-
Упорядоченное множество – в которых между элементами существует порядок (натуральный ряд чисел…);
Множество предметов и явлений ребенком воспринимается различными анализаторами.
1-2 года. К 1-2 годам у детей накапливаются представления о множестве однородных предметов, которые отражаются в пассивной речи детей (построить домик и домики – единственное и множественное число).
Затем в активной речи дети начинают использовать множественное и единственное число. На этом этапе множество еще не имеет четких границ для ребенка и не воспринимается элемент за элементом, не осознается количественная сторона множества.
Дети понимают смысл слова «много» и «мало», но эти слова не имеют четкой количественной характеристики, ассоциируются со словами «большой», «маленький».
2-3 года. Дети воспринимают множество в его границах, умеют сосредотачивать свое внимание на границах множества, а четкое понимание внутренних элементов еще отсутствует. При наложении предметов на рисунки дети заполняют всю часть карточки между крайними элементами, но не воспринимают количество. Легче воспринимают множество, если оно расположено линейно, в ряд.
3-4 года. Ребенок становится более требовательным к однородному составу множества, т.е. он считает, что множество всегда состоит из однородных элементов. На восприятие множества еще оказывают влияние качественно-пространственные признаки (форма, величина, расстояние между элементами, расположение по-разному в пространстве).
4-5 лет. На этом этапе восприятие только однородных множеств играет отрицательную роль, поэтому необходимо предлагать детям производить различные операции с множествами: составлять единое множество из 2-х групп, каждая из которых обладает своими качественными особенностями, несущественными для всего множества в целом.
Множества
обозначаются заглавными латинскими
буквами, а их элементы – строчными.
Запись a ![]() R означает,
что элемент а принадлежит
множеству R ,
то есть а является
элементом множества R .
В противном случае, когда а не
принадлежит множеству R ,
пишут a
R означает,
что элемент а принадлежит
множеству R ,
то есть а является
элементом множества R .
В противном случае, когда а не
принадлежит множеству R ,
пишут a ![]() R .
R .
Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А .
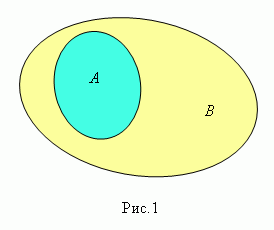
Говорят,
что множество А содержится
в множестве В ( рис.1 )
или множество А является подмножеством множества В ( в
этом случае пишут А ![]() В ), если
каждый элемент множества А одновременно
является элементом множества В .
Эта зависимость между множествами
называется включением.
Для любого множества А имеют
место включения:
В ), если
каждый элемент множества А одновременно
является элементом множества В .
Эта зависимость между множествами
называется включением.
Для любого множества А имеют
место включения: ![]()
![]() А
и А
А
и А ![]() А .
А .
Сумма
( объединение )
множеств А и В ( пишется А ![]() В )
есть множество элементов, каждый из
которых принадлежит либо А ,
либоВ.
Таким образом, е
В )
есть множество элементов, каждый из
которых принадлежит либо А ,
либоВ.
Таким образом, е ![]() А
А ![]() В тогда
и только тогда, когда либо
е
В тогда
и только тогда, когда либо
е ![]() А , либо е
А , либо е ![]() В .
В .
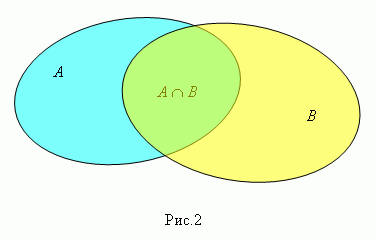
Произведение
( пересечение )
множеств А и В ( пишется А ![]() В ,
рис.2 ) есть множество элементов,
каждый из которых принадлежит иА ,
и В .
Таким образом, е
В ,
рис.2 ) есть множество элементов,
каждый из которых принадлежит иА ,
и В .
Таким образом, е ![]() А
А ![]() В тогда
и только тогда, когда е
В тогда
и только тогда, когда е ![]() А и е
А и е ![]() В .
В .
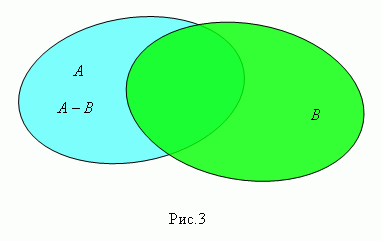
Разность множеств А и В ( пишется А – В , рис.3 ) есть множество элементов, которые принадлежат множеству А , но не принадлежат множеству В. Это множество называется также дополнением множества В относительно множества А.
Симметричная разность множеств А и В ( пишется А \ В ) есть множество:
А \ В = ( А – В ) ![]() ( В – А ).
( В – А ).
Свойства операций над множествами:

П р и м е р ы. 1. Множество детей является подмножеством всего населения.
2. Пересечением множества целых чисел с множеством поло-
жительных чисел является множество натуральных чисел.
3. Объединением множества рациональных чисел с множест-
вом иррациональных чисел является множество действи-
тельных чисел.
4. Нуль является дополнением множества натуральных чисел
относительно множества неотрицательных целых чисел.
