Е.Н. Грибанов Теория вероятностей и математическая статистика. Методические указания для студентов всех специальностей
.pdf
90
и |
|
z |
2 |
|
находятся |
по формулам z |
= 1 ln1 |
+rв − |
zα ; |
||||
|
|
|
|
|
|
|
|
1 |
−r |
n −3 |
|||
|
|
|
|
|
|
|
|
|
|
|
2 1 |
||
|
|
= 1 ln1 |
+rв + |
zα |
|
1 |
−α |
|
|
в |
|
||
z |
2 |
, где Ф(z )= |
. |
|
|
|
|||||||
|
|
|
|
|
|||||||||
|
2 |
1 |
−r |
n −3 |
α |
2 |
|
|
|
|
|||
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
Пример 52. Проверить значимость выборочного коэффициента корреляции из примера 51 и найти доверительный интервал с надёжностью 0,95 для него.
Решение. Для проверки значимости найдём статистику
t = r |
n −2 |
= 0,854 |
48 |
≈11,37 . По |
уровню |
значимости |
в |
1−r 2 |
|
1−0,8542 |
|
|
|
|
в |
|
|
|
|
|
α = 0,05 и числу степеней свободы k = 48 |
найдём |
tα ,k = 2,009 |
||||
(см. приложение табл.3). Так как t ≥ tα ,k , то нулевую гипотезу об
отсутствии корреляционной связи между переменными Х и У следует отвергнуть. Следовательно, выборочный коэффициент корреляции значим. Найдём доверительный интервал для выборочного коэффициента корреляции, вычислим
z = 1 ln1 |
+0,854 − |
1,96 |
≈ 0,9849 , z |
2 |
= 1 ln 1,854 |
+ 1,96 |
≈1,5566 , |
||
1 |
2 1 |
−0,854 |
50 −3 |
|
2 0 |
,146 |
47 |
|
|
|
|
|
|
||||||
тогда th z1 = th0,9849 ≈ 0,755 и th z2 = th1,5566 ≈ 0,9149 . Следова-
тельно, доверительный интервал для выборочного коэффициента корреляции имеет вид 0,755 < r < 0,9149.
58. Эмпирическая и теоретическая линии регрессии
Определить форму связи – значит выявить механизм получения зависимой случайной величины.
Кривой регрессии У по Х (или Х по У) называют условное среднее значение случайной величины У, рассматриваемое как функция определённого класса, параметры которой находятся методом наименьших квадратов по наблюдённым значениям двухмерной случайной величины. То есть уравнение линейной регрессии имеет вид y = β0 + β1x . Оценке в этом случае подлежат па-
раметры β0 и β1, называемые коэффициентами регрессии, а также σост2 - остаточная дисперсия. Остаточной дисперсией называ-
91
ется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака.
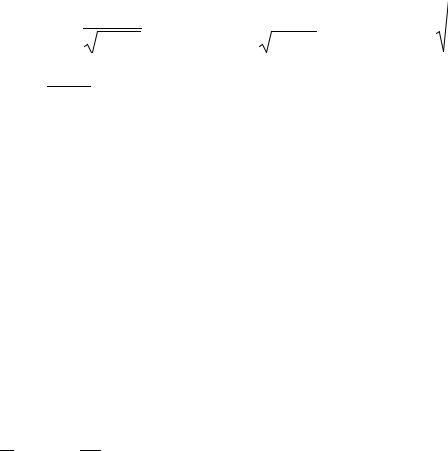
Пример 53. Построить эмпирическую и теоретическую линии регрессии по данным примера 51.
Решение. Уравнение теоретической линии регрессии имеет вид y = rв SS((xy))(x − x)+ y ,
где: x = hxu +C x = 2,2 (−0,04)+14,8 =14,792, y = hyv +C y = 6,3 0,24 +22,45 = 23,962 ,
S(x)= hx S(u)≈ 2,2 1,549 ≈ 3,408,
S(y)= hy S(v)≈ 6,3 1,422 ≈8,959 . Тогда уравнение регрессии име-
ет вид y = 0,854 83,,959408 (x −14,792)+23,962 или y = 2,245x −9,245.
Для построения возьмём точки (8,2;9,2) и (21,4;38,8). При по-
строении эмпирической линии регрессии используем точки вида (xi ; yi ), где значения yi находятся по формуле yi = hyvi +C y .
Получаем y1 = −2 6,3 +22,45 = 9,85,
y2 = −1,5 6,3 + 22,45 =13, y3 = −0,5 6,3 +22,45 =19,3, y4 = 0,5 6,3 +22,45 = 25,6 , y5 = 6,3 +22,45 = 28,75,
y6 = 43 6,3 +22,45 = 30,85 , y7 = 83 6,3 +22,45 = 39,25 . Построим на
плоскости точки с координатами (8,2;9,9), (10,4;13), (12,6;19,3),
(14,8;25,6), (17;28,8), (19,2;30,9), (21,4;39,3) и, соединив их в по-
рядке возрастания х, получим эмпирическую линию регрессии.
50
40
30
20
10
0
0 |
5 |
10 |
15 |
20 |
25 |
92
59. Значимость коэффициентов регрессии Проверить значимость оценок коэффициентов регрессии –
значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициенты регрессии отличны от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициентов регрессии, соблюдая предпосылки нормальной регрессии.
Вычисляем статистику t = |
|
b |
|
, которая имеет k = n −2 сте- |
|
Sb |
|||||
|
|
|
|||
пеней свободы, b – оценка коэффициента регрессии, Sb - оценка
среднего квадратического отклонения коэффициента, иначе стандартная ошибка оценки. По уровню значимости и числу степеней свободы по таблице находят tα ,k . Если t > tα ,k , то гипотезу о ра-
венстве нулю коэффициента регрессии отвергают, следовательно при заданном уровне значимости коэффициент регрессии значим. Оценки среднего квадратического отклонения находятся по фор-
мулам Sb |
= |
Sост |
, |
Sb = |
Sост |
, где S(x)= |
|
1 |
∑(xi − x)2 |
|
S(x) n − 2 |
n |
|||||||||
0 |
|
n −2 |
|
1 |
|
|
|
и Sост2 = n 1−2 ∑(yi − y(xi ))2 .
Доверительные интервалы для коэффициентов регрессии находятся по формулам b −tα ,k Sb < β < b +tα ,k Sb .
Пример 54. Найти коэффициенты регрессии, проверить их значимость и построить доверительные интервалы при уровне значимости α = 0,05 по данной выборке
xi |
|
1 |
|
2 |
3 |
|
4 |
|
|
5 |
|
6 |
7 |
8 |
9 |
10 |
|
||||
yi |
|
7 |
|
9 |
11 |
|
15 |
|
15 |
|
19 |
20 |
23 |
24 |
27 |
|
|||||
|
|
|
|
Решение. Найдём коэффициенты регрессии по формулам |
|||||||||||||||||
β |
= |
|
|
xy − x y |
и β |
0 |
= y − β |
1 |
x . |
Вычислим значения входящих в |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
|
|
x2 −(x)2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
формулы величин:
x = n1 ∑xi =101 (1+2 +3 +4 +5 +6 +7 +8 +9 +10)= 5,5,
|
|
|
|
|
|
|
|
|
|
93 |
|||
y = |
1 |
|
∑ yi |
= |
1 |
(7 +9 +11+15 +15 +19 +20 +23 +24 +27)=17 , |
|||||||
n |
|
||||||||||||
|
|
|
|
|
|
10 |
|
||||||
|
|
= |
|
|
|
1 |
|
(12 |
+22 +32 +42 +52 +62 +72 +82 +92 +102 )= 38,5 , |
||||
x2 |
|
|
|
||||||||||
10 |
|||||||||||||
|
|
|
|
(72 |
+92 +112 +152 +152 +192 +202 +232 +242 +272 )=329,6, |
||||||||
|
= |
|
|
|
1 |
|
|||||||
y2 |
|
|
|
||||||||||
10 |
|||||||||||||
|
|
|
|
|
|
|
|
||||||
xy =101 (7 +2 9 +3 11+4 15 +5 15 +6 19 +7 20 +8 23+9 24 +270)= =111,1.
Тогда β = |
111,1−5,5 17 |
≈ 2,13 и β |
0 |
=17 −2,13 5,5 ≈ 5,27 , следова- |
||
|
||||||
1 |
38 |
,5 |
−5,52 |
|
|
|
|
|
|
|
|||
тельно, уравнение регрессии имеет вид y = 2,13x +5,27 . Проверим значимость коэффициентов регрессии. Для этого вычислим
S(x)= 
x2 −(x)2 =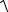 
38,5 −5,52 ≈ 2,872 . Найдём y(xi ), используя уравнение регрессии
y(1)≈ 7,4; y(2)≈ 9,53; y(3)≈11,66; y(4)≈13,79;
y(5)≈15,92; y(6)≈18,05; y(7)≈ 20,18; y(8)≈ 22,31; y(9)≈ 24,44; y(10)≈ 26,57 . Найдём остаточную дисперсию по формуле
S2 |
|
|
= |
|
1 |
|
|
∑(y −y(x ))2 = |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
n−2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
ост |
|
|
|
|
|
|
i |
|
i |
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
1 |
(0,42 +0,532 +0,662 +1,212 +0,922 +0,952 +0,182 +0,692 +0,442 +0,432)≈ |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≈0,622 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sост |
= 0,7887 |
|
|||||||||||
Вычислим |
|
Sост ≈ 0,7887 , |
тогда Sb |
= |
≈ 0,279 и |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Sост |
= 0,7887 |
|
|
0 |
|
n − 2 |
8 |
|
|||||||||||||
Sb |
|
= |
|
|
≈ 0,097 . |
|
Статистики |
равны |
|||||||||||||||||||||
|
|
1 |
|
|
S(x) |
|
|
|
|
n − 2 |
2,872 |
8 |
|
|
|
|
|
|
|
|
|
||||||||
t |
0 |
= |
|
β0 |
|
= |
|
|
5,27 |
|
|
≈18,9 |
и |
t = |
|
β1 |
|
|
= |
2,13 |
≈ 21,96 . По таблице |
||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
Sb |
|
|
|
|
|
0,279 |
|
|
|
|
1 |
|
Sb |
|
0,097 |
|
|
|
||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
tкр(8; 0,05)= 2,31. |
Так как |
||||
(см. |
|
приложение |
|
табл. |
5) |
находим |
|||||||||||||||||||||||
t0 > tкр и t1 > tкр, то оба коэффициента значимы. Доверительный интервал для b0 имеет вид
|
|
94 |
|
|
|
5,27 − 0,279 2,31 < b0 < 5,27 + 0,279 2,31 |
или |
4,626 < b0 < 5,914 . |
|||
Доверительный |
интервал |
для |
b1 |
имеет |
вид |
2,13 − 0,097 2,31 < b1 < 2,13 + 0,097 2,31 или 1,906 < b1 < 2,354 . |
|
||||
60. Корреляционное отношение На практике часто предпосылки корреляционного анализа
нарушаются: один из признаков оказывается неслучайным, или признаки не имеют нормального распределения. Однако статистическая связь между ними существует. Для изучения связи между ними в этом случае существует показатель зависимости признаков, основанный на показателе изменчивости общей (или полной) дисперсии.
Полной называется дисперсия признака относительно его
математического ожидания. Так |
для признака У это |
σ 2y = M (Y − M (y))2. Дисперсию σ 2y |
можно разложить на две со- |
ставляющие, одна из которых характеризует влияние фактора Х на У, другая - влияние прочих факторов. Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной.
По выборочным данным рассчитываем выборочное корреля-
S 2y
ционное отношение η2 = |
|
x |
, где |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
S 2y |
|
|
|
|
|
|
|
|
S 2 |
|
∑ y2m y |
|
∑ yi m y |
|
2 |
|
|
|
1 |
∑(y(x |
)− y)2 m |
|
|
= |
i |
− |
|
|
и S |
y |
= |
|
x |
. Зна- |
||||
|
|
|
||||||||||||
y |
|
∑m y |
|
∑m y |
|
|
|
|
∑m |
i |
|
|
||
|
|
|
|
|
|
x |
|
|
|
|
|
|||
чения η2 лежащие в интервале 0 ≤η2 ≤1, являются показателями тесноты группировки точек около кривой регрессии независимо
от её вида (формы связи). Корреляционное отношение η2 связано с r 2 следующим образом: 0 ≤ r 2 ≤η2 ≤1. В случае линейной зависимости между переменными: r 2 =η2.
95
Задачи для самостоятельной работы Задача 1 Сколькими способами из 8 человек можно избрать
комиссию: а) в составе трёх человек; б) составе председателя, его заместителяисекретаря?
Задача 2. Брошены две игральные кости. Найти вероятности следующих событий: а) сумма выпавших очков равна семи; б) сумма выпавших очков равна восьми, а разность - четырём; в) сумма выпавших очков равна восьми, если известно, что разность равна четырём; г) сумма выпавших очков равна пяти, а произведение – четырём.
Задача 3. а) Каждая из букв т, м, р, о, ш написана на одной из пяти карточек. Карточки перемешиваются и раскладываются наугад в ряд. Какова вероятность того, что образуется слово «шторм»? б) Из букв разрезанной азбуки составлено слово «ремонт». Перемешаем карточки, затем, вытаскивая их наудачу, кладём в порядке вытаскивания. Какова вероятность того, что при этом получится слово «море»?
Задача 4. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлечённый кубик имеет окрашенных граней: а) одну; б) две; в) три.
Задача 5. Монета брошена два раза. Найти вероятность того, что хотя бы один раз появится «герб».
Задача 6. Из колоды в 52 карты вынимаются наудачу три карты. Найти вероятность того, что это тройка, семёрка, туз.
Задача 7. За круглым столом сидят 5 мужчин и 5 женщин. Какова вероятность того, что два лица одинакового пола не сидят рядом, если места занимаются случайно?
Задача 8. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
Задача 9. Колоду карт, состоящую из 36 карт, наудачу разделяют на две равные части. Чему равна вероятность того, что в обеих частях окажется по равному числу красных и чёрных карт?
Задача 10. В урне 3 белых и 7 чёрных шаров. Какова вероятность того, что вынутые наугад два шара окажутся чёрными.
Задача 11. В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Най-
96
ти вероятность того, что среди отобранных лиц окажутся три женщины.
Задача 12. На складе имеется 15 кинескопов, причём 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода.
Задача 13. В группе 12 студентов, среди которых 8 троечников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять троечников.
Задача 14. В шкафу находится 10 пар ботинок различных сортов. Из них случайно выбирается 4 ботинка. Найти вероятность того, что среди выбранных ботинок отсутствуют парные..
Задача 15. Найти вероятность того, что дни рождения 12 человек придутся на разные месяцы года.
Задача 16. Территория нефтебазы имеет форму прямоугольника со сторонами 50 м и 30 м. На территории имеется 4 круглых нефтебака, диаметром 10 м каждый. Какова вероятность поражения нефтебаков бомбой, попавшей на территорию нефтебазы, если попадание бомбывлюбуюточку равновероятно.
Задача 17. В круг вписан квадрат. Какова вероятность того, чтоточка, брошенная наудачу вкруг, окажется внутриквадрата?
Задача 18. Наудачу взяты два положительных числа x и y , каждое из которых не превышает двух. Найти вероятность того,
что произведение x y будет не больше единицы, а частное y x
не больше двух.
Задача 19. Найти вероятность того, что из трёх отрезков не превосходящих по длине а можно построить треугольник.
Задача 20. Два стрелка стреляют в цель и делают по одному выстрелу. Вероятность попадания в цель первым стрелком равна 0,5, вторым - 0,7. Какова вероятность того, что оба стрелка попадут в цель?
Задача 21. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.
Задача 22. В одном ящике 5 белых и 10 красных шаров, в другом ящике 10 белых и 5 красных шаров. Найти вероятность то-
97
го, что хотя бы из одного ящика будет, вынут один белый шар, если из каждого ящика вынуто по одному шару.
Задача 23. Вероятность хотя бы одного попадания при двух выстрелах равна 0,99. Найти вероятность промаха при одном выстреле.
Задача 24. Предположим, что для одной торпеды вероятность потопить корабль равна 1/2. Какова вероятность того, что 4 торпеды потопят корабль, если для потопления корабля достаточно одного попадания торпеды в цель?.
Задача 25. В ящике 10 красных и 6 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность того, что пуговицы будут одноцветными?
Задача 26. Вероятность попадания в самолёт равна 0,8, а вероятность его сбить 0,32. Найти вероятность того, что при двух попаданиях самолёт будет сбит.
Задача 27. В урне 10 шаров. Вероятность вытаскивания двух чёрных равна 2/15. Сколько в урне было белых шаров?
Задача 28. Студент пришёл на зачёт, зная из 30 вопросов только 24. Какова вероятность сдать зачёт, если после отказа отвечать на первый вопрос преподаватель задаёт ещё один вопрос?
Задача 29. В ящике лежат 12 красных, 8 зелёных и 10 синих шаров. Наудачу вынимаются два шара. Найти вероятность того, что будут вынуты шары разного цвета, при условии, что не вынут синий шар.
Задача 30. Студент, разыскивая книгу, решил обойти три библиотеки. Для каждой из библиотеки одинаково вероятно, есть
веё фондах книга или нет, если есть, то одинаково вероятно, выдана она или нет, что вероятнее, достанет студент книгу или нет.
Задача 31. Часы изготовляются на трёх заводах и поступают
вмагазин. Первый завод производит 40% продукции, второй - 45% и третий - 15%. В продукции первого завода спешат 80% часов, у второго - 70% и у третьего - 90%. Каково вероятность того, что купленные часы спешат?
Задача 32. По самолёту производится три выстрела. Вероятность попадания при первом выстреле равна 0,5, при втором - 0,6, при третьем - 0,8. При одном попадании самолёт будет сбит с вероятностью 0,3, при двух - с вероятностью - 0,6, при трёх - самолёт будет сбит наверняка. Какова вероятность того, что самолёт будет сбит?
98
Задача 33. Шесть шаров, среди которых 3 белых и 3 чёрных, распределены по двум урнам. Наудачу выбирается урна, а из неё - один шар. Как нужно распределить шары по урнам, чтобы вероятность события А = {вынутый шар белый} была максимальной.
Задача 34. Программа экзамена содержит 30 различных вопросов, из которых студент Иванов знает только 15. Для успешной задачи экзамена достаточно ответить на 2 предложенных вопроса или на один из них и на дополнительный вопрос. Какова вероятность того, что Иванов успешно сдаст экзамен?
Задача 35. Студент знает 20 из 25 вопросов программы. Зачёт считается сданным, если студент ответит не менее чем на три из чётырёх поставленных в билете вопросов. Взглянув на первый вопрос, студент обнаружил, что он его знает. Какова вероятность того, что студент сдаст зачёт.
Задача 36. (задача де Мере). Сколько раз нужно бросить пару игральных костей, чтобы с вероятностью, не меньшей 0,5, хотя бы один раз появилась сумма очков, равная 12?
Задача 37. В спартакиаде участвуют: из первой группы 4 студента, из второй - 6 и из третей - 5. Студент первой группы попадает в сборную института с вероятностью 0,9, для студента второй группы эта вероятность равна 0,7, а для студента третьей группы - 0,8. Наудачу выбранный студент попал в сборную института. В какой группе, вероятнее всего, учится этот студент.
Задача 38. Из полного набора костей домино 28, наугад берутся две кости. Определить вероятность того, что вторую кость можно приставить к первой.
Задача 39. Два стрелка независимо один от другого стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8, для второго - 0,4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что в мишень попал первый стрелок.
Задача 40. В урне лежит шар неизвестного цвета - с равной вероятность белый или чёрный. В урну опускается один белый шар и после тщательного перемешивания наудачу извлекается один шар. Он оказался белым. Какова вероятность того, что в урне остался белый шар.
Задача 41. Мимо бензоколонки проезжают легковые и грузовые машины. Среди них грузовых машин 60%. Вероятность того, что проезжающая машина подъедет на заправку для грузовых ма-
99
шин, равна 0,1, а для легковых - 0,2. К бензоколонке подъехала на заправку машина. Найти вероятность того, что она грузовая.
Задача 42. Три стрелка одновременно выстрелили, и в мишени обнаружили две пули. Найти вероятность того, что третий стрелок поразил мишень, если вероятность попадания в мишень для первого стрелка равна 0,6, для второго - 0,5, а для третьего - 0,4.
Задача 43. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключён): три партии из четырёх или пять из восьми.
Задача 44. Вероятность появления события А в опыте равна 0,3. Опыт повторили 5 раз независимым образом. Какова вероятность того, что событие А при этом появится не менее двух раз?
Задача 45. В стройотряде 70% первокурсников и 30% студентов второго курса. Среди первокурсников 10% девушек, а среди студентов второго курса - 5% девушек. Все девушки по очереди дежурят на кухне. Найти вероятность того, что в случайно выбранный день на кухне дежурит первокурсница.
Задача 46. Батарея дала 14 выстрелов по объекту, вероятность попадания в который равна 0,2. Найти наивероятнейшее число попаданий и вероятность этого числа попаданий.
Задача 47. Вероятность попадания в цель при каждом выстреле из орудия равна 0,8. Сколько нужно произвести выстрелов, чтобы наивероятнейшее число попаданий было равно 20.
Задача 48. Средняя плотность болезнетворных микробов в одном кубическом метре воздуха равна 100. Берется на пробу 2 дм3 воздуха. Найти вероятность того, что в нём будет обнаружен хотя бы один микроб.
Задача 49. Сколько в среднем нужно класть изюма в булочку, чтобы вероятность найти хотя бы одну в ней превышала 0,95.
Задача 50. Случайная величина Х распределена по закону, определяемому плотностью распределения вероятностей вида:
c cos x, при π |
|
≤ x ≤ π |
|
, |
||
f (x)= |
при |
2 |
x > π |
|
2 |
|
0, |
|
2 |
. |
|
||
|
|
|
|
|
|
|
Найти константу с, вычислить P{x < π 4 , М(х) и D(х).