Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кузбасский государственный технический университет

Предмет:

Высшая математика

Файл:

Г.В. Алексеевская Использование графиков при решении задач, уравнений, неравенств и систем

.pdf

Скачиваний:

Добавлен:

19.08.2013

Размер:

396.71 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ

КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра высшей математики

ИСПОЛЬЗОВАНИЕ ГРАФИКОВ ПРИ РЕШЕНИИ ЗАДАЧ, УРАВНЕНИЙ, НЕРАВЕНСТВ И СИСТЕМ Методические указания по курсу «Математика»

для студентов направления подготовки 550100

Составители Г.В. Алексеевская Г.А. Липина Н.Г. Шевелева

Утверждены на заседании кафедры Протокол №5 от 07.06.01

Рекомендованы к печати методической комиссией по направлению 550100 Протокол №38 от 10.09.01

Электронная копия хранится в библиотеке главного корпуса ГУ КузГТУ

Кемерово 2002

В предлагаемых методических указаниях авторы рассматривают графический метод решения примеров и задач, вызывающих затруднения на вступительных экзаменах по математике у абитуриентов Кузбасского государственного технического университета.

Указания предназначены для старшеклассников, готовящихся к поступлению в ВУЗ, а также могут быть полезны для учителей средней школы.

Графиком Г-функции у = f(x) называется множество точек плоскости с координатами (x, f(x)), где x принадлежит области определения функции y . Предпола-

гаем, что читатель знаком с основными элементарными функциями, а также уравнениями кривых второго порядка:

1)линейной - y = x ;

2)обратно пропорциональной - y =1 / x ;

3)	степенной - y = xa , a R;
4)	показательной - y = ax , a >0 ,	a ≠ 1;
5)	логарифмической - y = loga x ,	a >0 , a ≠ 1;
6)	тригонометрическими - y = sin x ; y = cos x ; y = tg x , y = ctg x ;

7)обратными тригонометрическими - y = arcsin x ; y = arccos x ;

y = arctg x ; y = arcctg x .

8)окружностью – x2 + y2 = R2 c центром в точке (0, 0), радиуса R;

9)эллипсом – х2/а2+y2/b2=1 c центром в точке (0, 0), полуосями: a − по оси

OX; b − по оси OY;

10)	гиперболой – x2 / a2 − y2 / b2 = 1 c центром в точке (0, 0), полуосями a
− действительной по оси ОX, b − мнимой по оси ОY;
11)	параболой – y2 = 2 px , с вершиной в точке (0,0), параметром p .

Напомним случаи, когда при построении графиков функций используются операции отображения, сдвига и деформации:

1)график функций y1 = − f ( x ) – отображение Г относительно оси ОX;

2)y2 = f ( −x ) − отображение Г относительно оси 0Y;

3)	y3	= f ( x −a ) − cдвиг Г по оси ОX на a вправо, если a > 0; влево, если a < 0;
4)	y4	= f ( x ) +b – сдвиг Г по оси ОY на b вверх, если b > 0; вниз, если b < 0;
5)	y5 = f ( ax ); a > 0; a ≠ 1 − сжатие в а раз при а > 1, растяжение в 1/ a раз (при
a <1) Г по оси ОX;
6)	y6		= bf ( x ), b > 0; b ≠ 1 − растяжение в b раз при b > 1, сжатие в 1/b раз (b < 1)
Г по оси ОY.
		Рассмотрим построение графиков функций:
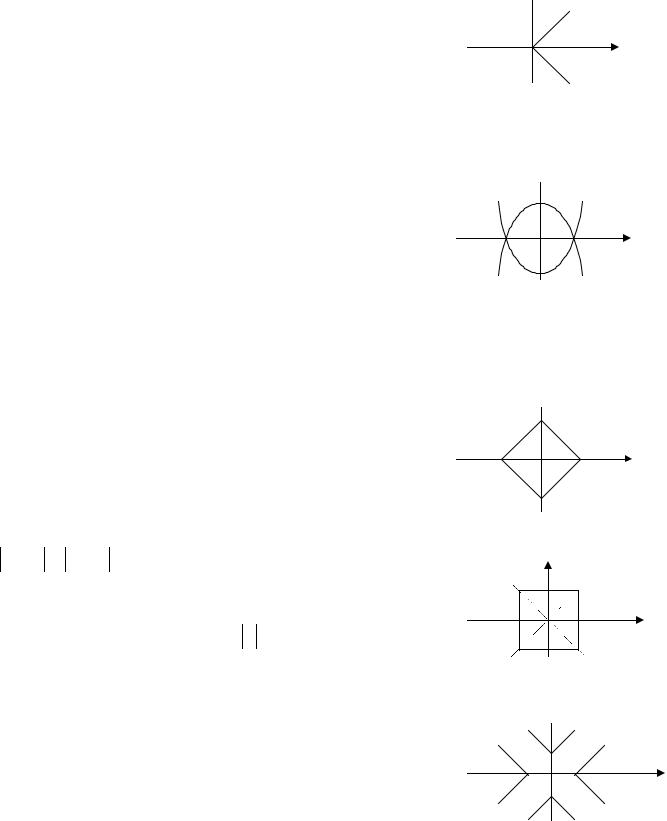
	1.		y =	x	=	− x	- симметричен относитель-
	1.		y =	x	=	− x	- симметричен относитель-		у
но оси ОY, т.е. построив график функции y = x при									у
но оси ОY, т.е. построив график функции y = x при
x > 0 , отобразим его на область x < 0 симметрично;
график расположен в верхней полуплоскости (рис. 1).										х
								Рис. 1		х
								Рис. 1

			3
2.	y	= x	симметричен относительно оси ОX,
2.	y	= x	симметричен относительно оси ОX,

располагается в правой полуплоскости (рис. 2). То есть при построении графиков функций, содержащих модули, удобно воспользоваться симметрией. Учитывая последнее замечание, построим графики функций:

x2 −2

−3

x > 0 , тогда имеем

Рассмотрим

область y > 0 ,

y = x2 −2x −3 = (x −1)2 −4 или

(x −1)2 = y +4 –

парабола с вершиной в точке (1, -4), ветви которой направлены вверх. С учетом того, что y > 0 , x > 0

отобразим график, лежащий ниже оси ОХ на верхнюю полуплоскость. Воспользовавшись симметрией, отобразим полученный график на y < 0, а затем на x < 0

(рис. 3).

4.	x	+	y	=1.

		Очевидно, что график симметричен относительно
ОХ и OY. Достаточно построить в области					y > 0 , x > 0
и	отобразить. В области x > 0 , y > 0				будем иметь

y = −x +1. Это прямая, проходящая через точки (1, 0) и

(0, 1). Далее делаем симметричное отображение полученного графика, результат представлен на рис. 4.

5. x + y + x − y =1.

График	симметричен	относительно	линий:
x + y = 0; x − y = 0, т.е. y = −x ;		y = x . Построим график

для области y > x , y > −x ( y > x ), в этой области имеем

функцию:

x + y − x + y =1,

т.е. 2 y =1; y =1 / 2 . После

отображения получаем график, изображенный на рис. 5.

−

=1.

График функции симметричен относительно линий:

х=0, у=0.

Построим график

для области x > 0 ,

y > 0 ;

x − y

=1. Из

определения

модуля

имеем: при

x > y

x − y

=1;

при

x < y y − x =1: две

прямые в

первом

Рис. 2

Рис. 3

1 х

Рис. 4

2у

1/2 х

Рис. 5

Рис. 6

квадрате, далее делаем отображение на оставшиеся квадранты (рис.6).

В некоторых случаях для построения графика исходную функцию удобнее разложить на сумму нескольких функций:

7. у= 2-х + 2+х .					у1	у
Заметим, что у>0. Введем функции y1 = 2-х ,					у2	у2	у1

y2 = 2+х , тогда у=у1+у2. Строим y1				и y2 . Гра-
фик функции y1 строим, сместив y = x				по оси ОХ			х
						Рис. 7
на 2 вправо;	график	y2	получаем	смещением

графика y = x	на 2 влево по оси ОХ (рис. 7). Далее
суммируем по точкам (рис. 8).						у	у=у1+у2
Применим графический метод к решению
уравнений, неравенств и систем.

8. 1+3х - х-1 =2–х.	х
8. 1+3х - х-1 =2–х.	Рис. 8
Решением уравнения будут	точки пересечения

графиков y1 = 1+3х - х-1 и y2 = 2 − x . В свою очередь: y1 = y3 + y4 ; у3= 1+3х =3 х+1/3 ; у4=- х-1 , т.е. имеем случай аналогичный №7 (рис. 9).

Из рисунка видно, что решений два: х1 и х2. Чтобы найти точные решения х1 и х2, запишем уравнения прямых графика функции у1 (рис.9, а; 9, б).

А у

у
у3
		у1
		С
		х
	у4	у2	х
	у4	В
Рис. 9,а		В
Рис. 9,а		Рис. 9,б
		Рис. 9,б

АВ: y1 =-3х –1+х–1=-2х–2=-2(х+1). Имеем: 2–х=-2(х+1); х1=-4.

ВС: y1 = 3x +1 + x −1 = 4x ; 2 − x = 4x ; x2 = 2 / 5 .

Ответ: х1=-4; х2=2/5.

9. 2x −1 −3 ≤ x +2 .

Обозначим y1 = 2 x −1/ 2 −3 ;

y2 = x +2 .

Очевидно,

что

x +2 ≥ 0 ,

т.к.

неотрицательное число не может быть меньше

отрицательного, т.е.

x ≥ −2. График

- это

х1

х2

х3

х4

y = x

смещенный

график

функции

точку

-3

(1/2, -3) с коэффициентом сжатия 2. Учитывая, что

y1 > 0 , часть графика, лежащую ниже оси ОХ,

Рис. 10

отображаем в верхнюю полуплоскость (рис. 10).

Тогда с y1 имеем четыре точки

пересечения. Область, где

y1 ≤ y2 изображена на


рис.10 штриховкой, т.е.		x1 < x < x2 и	x3 < x < x4 .		Находим численные значения
x1, x2 ,	x3 , x4 : x1	находим как	пересечение		y2 = x +2 с прямой АВ:
y1 = −2(x +1) , имеем −2x −2 = x +2 ; 3x = −4 ;				x = −4 / 3. x2 находим как пере-
сечение	y2 = x +2 с прямой ВС: y1 = 2(x +1) ;			x +2 = 2x +2; x2 = 0. x3 нахо-

дим как пересечение y2 = x +2 с прямой СD:

y1 = −2(x −2) ;

−2x +4 = x +2 ;

−3x = −2;

x3 =2/3. x4 находим

как

пересечение

y2 = x +2

прямой

DЕ:

y1 = 2(x −2); 2x −4 = x +2 ; x4 = 6.

Ответ: -4/3 ≤ х ≤ 0: 2/3 ≤ х ≤ 6.

+ x

−2 = 4,

10.

=8.

y − x

y = 4 − x −2 -

График функции

смещенный в

y = x ,

точку

(2,

график

функции

лучами

направленный

вниз. Заметим,

что

график

функции

у2

y − x =8

располагается

полуплоскостях

у>х,

у1

y1 =8 + x

и y < x , у2=х–8 (рис. 11). Очевидно точка

-8

пересечения единственная:

y = x −8

−

-8

= −x +

Рис. 11

0 = 2x −14.

Ответ: x =7 , y = −1.

Рассмотрим построение графиков, состоящих из ветвей парабол.

11. y = x2 + x −	x	.	y = x2
11. y = x2 + x −	x	.
Построим	для x >0 :			параболу с
вершиной в	точке (0,		0);	для	x <0 :
y = x2 + 2x = x2 + 2x +1 −1 =( x +1 )2 −1					–	х

параболу с вершиной в точке (-1, -1), (рис. 12).

Рис. 12

12. y = x2 + x −1.

Перепишем:

y = x2 + x +1 / 4 −1 / 4 −1 = (x +1 / 2)2 −1. График этой функции удобно по-

строить, сдвинув на –1 по оси ОУ график функции

y	=	(x +1 / 2)2		−1	/ 4	,	y ≥0 , опустив модуль,

1							1
имеем			уравнение		параболы с			вершиной
(-1/2,			-1/4).	Для			получения	графика
y	=	(x +1 / 2)2		−1	/ 4		часть	параболы,

1

лежащую ниже оси ОХ, отобразим на верхнюю полуплоскость (на рис. 13 у1 обозначен штрихами,

у= y1–1 – сплошной линией).

13. y = x2 −2 x −3 .

Для построения графика этой функции удобно воспользоваться симметрией. Так как график функции

y = x симметричен по оси ОY, x = y симметричен по

оси ОХ, удобно рассмотреть функцию в области x > 0 , y > 0 и полученный график отобразить на остальные

четверти. При x > 0 ,				y > 0 будем иметь:
y =	x2 −2x −3	=	(x −1)2 −4		парабола с вершиной в

1/2 у1

Рис. 13

Рис. 14

точке (1, -4), нижняя часть которой отображена в верхнюю полуплоскость (рис. 14).

Решить уравнения.

14. x2 + 2x + x2 + x = 5 .

Перепишем уравнение:

х2+2х+1-1 =-(х2+х+1/4-1/4)+5; (х+1)2-1 =-(х+1/2)2+21/4.

y1 =	( x +1 )2 −1	.	у2=-(х+1/2)2+21/4.		Решением являются
точки пересечения графиков у1				и y2	(рис. 15.), т.е. решим
аналитически: x2 + 2x = −x2 − x −5 . 2x2 + 3x + 5 =0 .
x1,2 = (−3 ± 9 +40 )= (−3 ±7)				= −5	; 1.
4			4	2

Ответ: х1 = -5/2, х2 = 1.

Рис. 15

15.

x +6

x −9 +

x −6

x −9 = 6.

Область допустимых значений: х≥9. Введем пере-

менную

x −9 =t ;

x −9 = t2 ; x = t2 + 9 х=t2+9; t≥0.

Тогда имеем:

t 2 +9 +6t

t 2 +9 −6t

= 6;

(t +32 )+

(t −32 )

= 6 или t+3 =6- t-3 .

Последнее уравнение решим графически (рис.16).

3≤t≤3, т.к. на этом участке y1 совпадает с

y2 с уче-

том, что t ≥ 0 , x −9 ≤3.

Решим неравенство графически:

y1 =

x −9 ;

y2 =3 (рис. 17), y1 = y2 ;

x −9 = 9 ;

x =18 .

9 ≤ x ≤18 .

Ответ:

	у
у1		у2
у1		у2

Рис. 16.

9	18	х
	Рис. 17

16. Решить неравенство:

x −7 ≤3 − x −4 .

у1

Решим графически. Область допустимых

значений: x

≤ 4 . Введем функции:

у2

y2 =3 −

у1= х-7 ;

x −4

(рис.

18). у2≥0;

х1

х2

x1 ≤ x ≤ x2 .

находим

из

уравнения:

Рис. 18

7 − x =3 −

x −4 ; 4 − x = −

x −4 ; 16-8х+х2=х-4;

9 ±

=5; 4 .

х2-9х+20=0;

81−80

находим

из

уравнения

1,2

x −7 =3 −

;

x −10 = −

x −4 ; х<10,

т.к. левая часть отрицательна, имеем

x −4

после

возведения

обеих

частей в

квадрат: x2 − 20x +100 = x −4 ;

x2 − 21x +104 =0 ;

x =

21±

441−416

21±5

=13; 8.

1,2

2≤ x ≤8 .

Ответ: 5

17. 3 x +1 −3 ≥ x2 −2x −3 .

Решение начинаем с области допустимых значений:

1)х+1≥ 3 – решаем неравенство графически (рис. 19). x ≤ −4, x ≥ 2 ;

2)x −2x −3 ≥ 0; (x −1)2 −4 ≥ 0 , (рис. 20) x ≥3; x ≤ −1.

		у			у
				-1	3	х	-4		2
-4	-1	2	х	-3				-1	3
	Рис. 19				Рис. 20			-1	3
	Рис. 19				Рис. 20			Рис. 21.

Таким образом, имеем область допустимых значений Возвращаемся к основному неравенству. Возведем

обе части в квадрат, получаем: 9( х+1 -3) ≥ х2-2х-3. Решим это неравенство графически (рис. 22.):

у1=9 х+1 -27;

y2 =(х-1)2–4,

т.е. у1 пересекает y2 в

одной точке, которую находим из уравнения:

9 (х+1) –27=х2-2х-3; х2-11х+15=0;

x =11±

11±

;

11±

<3.

121−60

1,2

Ответ: 3 ≤ x ≤( 11 + 61 ) / 2 .

x ≥ 3 ; x ≤ −4 (рис. 21).

Рис. 22.

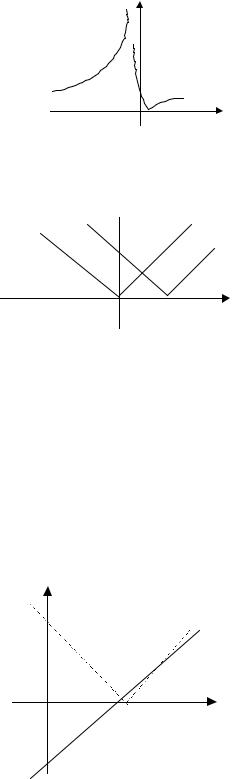
Рассмотрим график дробно-линейной функции. 18. у= (2х-3)/(х+2) .

Перепишем функцию:

у= (2х-3)/(х+2) = {2(х-3/2+2-2)} /(x+2) = {2(x+2)-(7/2)·2}/(x+2) = 2-7/(x+2) .

График этой функции получаем, смещая центр гиперболы в точку (-2, 2) с учетом, что коэффициент сжатия (-7), т.е. график располагается во второй и четвертой четвертях, причем часть гиперболы, лежащая ниже оси ОХ, отображается в верхнюю плоскость

(рис. 23).

19. (3х+1)/(х-3) <3.

ОДЗ: x ≠ 3. Умножим обе части неравенства на положительное число х-3 , будем иметь:

3х+1 <3 х-3 ; 3 х+1/3 <3 х-3 .

Знак неравенства не меняется. Построим графики у1= х+1/3 и у2= х-3 . Очевидно, что у1< y2 при x < x0 , x0 найдем из пересечения прямых:

x +1 / 3 = −x + 3 ; 2x = 3 −1 / 3; x		=	8	=	4
x +1 / 3 = −x + 3 ; 2x = 3 −1 / 3; x		=	2 3	=	3
(рис. 24).	0		2 3		3
(рис. 24).	4 .
Ответ: x <	4 .
	3

Рис. 23

х0 х

Рис. 24.

Графический метод используют при решении уравнений, содержащих параметр. Рассмотрим следующие примеры:

20. При каких значениях	a уравнение:			ax −4	= x −3 имеет два решения?

Введем обозначения	y1 =	ax −4	;	y2 = x −3. Построим график функции y2

(рис.25). График у1>0 получаем отображением прямой у=ах-4, лежащей ниже оси ОХ, в верхнюю полуплоскость, a – угловой коэффициент;

a=tgα, где α - угол наклона прямой. Очевидно, что вершина графика ах-4 должна лежать между

точками (3, 0)	и (4, 0), левая ветвь проходит через
точку (0, 4),	a >0, т.к. если a <0, то решений нет;

при a =1 – одно решение, т.к. отображенный угол у1 параллелен графику у2; при a =4/3 – множество

решений, т.к. луч у1 совпадает с y2 .

Ответ: 1<a<4/3.

у
у1
у2	х
Рис. 25

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете Высшая математика