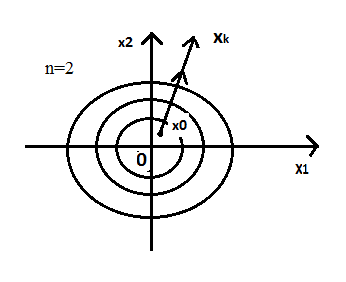
- •1. Записать решение однородной системы дифференциальных уравнений с постоянными коэффициентами, представленной в форме Коши, в скалярной и матричной формах.
- •2. Что выражает общее и частное решение системы дифференциальных уравнений в теории управления:
- •3. Показать, каким образом экспоненциальная матрица записывается степенным рядом
- •5. Получить систему линеаризованных уравнений состояния обьекта и систему уравнений наблюдения разложением в ряд Тейлора в окрестности рабочего режима
- •6. Получить систему линеаризованных уравнений состояния обьекта в пространстве состояний при малых отклонениях
- •7.Получить линеаризованные математическое описание динамической системы первого приближения, если нелинейные функции допускают разложение их в степенные сходящиеся ряды.
- •8. Как определяются собственные числа матрицы? Показать прямой метод определения собственных векторов матрицы.
- •9. Как можно сформулировать устойчивость системы на физическом уровне без использования критериев устойчивости?
- •12. Показать процедуру диагонализации илипроцедуру приведения математического описания системы к каноническому виду.
- •14.Привести квадратичную форму и ее свойства. Критерии Сильвестора.
- •15. Сформулировать теоремы второго (прямого) метода а.М.Ляпунова об устойчивости движения динамической системы. . Привести геометрическую интерпретацию.
- •16.Привести построение функции а.М.Ляпунова для линейных систем.
- •17.Привести определения устойчивости динамической системы в малом в большом в целом
- •18. Показать между математическим описанием динамической системы в пронстранстве состояний в обычной форме математическим описанием системы в канонической форме.Сделать соответствующий вывода
14.Привести квадратичную форму и ее свойства. Критерии Сильвестора.
Квадратичная форма
Пусть
задана линейная динамическая система
следующего вида: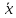 = Ax
+ Bu
, u(t)
º 0
.
= Ax
+ Bu
, u(t)
º 0
.
Рассмотрим
свободную систему вида: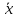 = Ax
= Ax
Выберем функцию следующего вида: V = xT Px , (1.2.10) где P( n× n ) – постоянная матрица; причем PT = P –симметрическая матрица, т. е. Pij = Pji ∀i, j = 1, n .
Квадратичную форму (вида 1.2.10) будем рассматривать в качестве функции Ляпунова, но прежде рассмотрим свойства квадратичной формы.
Свойства квадратично формы
Критерии Сильвестра
Критерии 1. Квадратичная форма является знака определенной положительной, если все главные диагональные миноры матрица P положительный.
Матрица P>0 –матрица P положительно определение, т.е.
P11
>0, P11
P12
>0;… det
P>0.
P21 P22
Критерии 2. Квадратичная форма является знака определенной отрицательной, если знаки главных диагональных миноров чередуются, начиная с отрицательного знака.
Матрица P<0 –матрица P положительно определение, т.е.
P11
>
0, P11
P12
>0; P11
P12
P13
… det P>0.
P21 P22 P21 P22 P23 <0 и т.д.,
P31 P32 P33
Т.е знаки чередуются, начиная с отрицательного знака.
15. Сформулировать теоремы второго (прямого) метода а.М.Ляпунова об устойчивости движения динамической системы. . Привести геометрическую интерпретацию.
Теоремы ВТОРОГО метода Ляпунова.Привести геометрическую интерпритацию
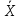 =F(x1,
x2,…….xn)
(1.2.9.a)
=F(x1,
x2,…….xn)
(1.2.9.a)
Теорема
1. Если для системы (1.2.9.a)
существует знакоопределенная положительная
функция V(x)
в
области Д, полная производная которой
по времени
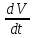 , взятая
в силу системы
(1.2.9.a),
является функцией знакоопределенной
отрицательной; то невозмущенное движение
х=0
асимптотический устойчиво по Ляпунову.
, взятая
в силу системы
(1.2.9.a),
является функцией знакоопределенной
отрицательной; то невозмущенное движение
х=0
асимптотический устойчиво по Ляпунову.
Если функция V(x) удовлетворяет условиям определения 2, то есть функция V(x) является знакоопределенной положительной:
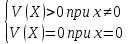
∫- значит в одной системе.
А
ее полная производная
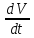 является знакоопределенной
отрицательной. Т.е.
является знакоопределенной
отрицательной. Т.е.
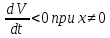 ,Где
,Где
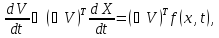
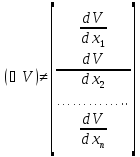 градиент
скалярной функции V(x)
градиент
скалярной функции V(x)
Где
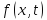 -правая
часть уравнения
(1.2.9.a),
то невозмущенное движение асимптотический
устойчиво по Ляпунову,
то есть lim
x(t)=0
при t→∞
-правая
часть уравнения
(1.2.9.a),
то невозмущенное движение асимптотический
устойчиво по Ляпунову,
то есть lim
x(t)=0
при t→∞
 Теорема
2. Если для системы (1.2.9.a)
существует в
области Д знакоопределенная
положительная функция V(x),
полная
производная которой по времени
Теорема
2. Если для системы (1.2.9.a)
существует в
области Д знакоопределенная
положительная функция V(x),
полная
производная которой по времени
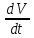 , взятая
в силу системы
(1.2.9.a)
является функцией знакоопостоянной
отрицательной; то невозмущенное движение
х=0
устойчиво
по Ляпунову.
, взятая
в силу системы
(1.2.9.a)
является функцией знакоопостоянной
отрицательной; то невозмущенное движение
х=0
устойчиво
по Ляпунову.
Если
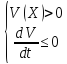 то
невозмущенное
движение
устойчиво по Ляпунову,
причем
то
невозмущенное
движение
устойчиво по Ляпунову,
причем
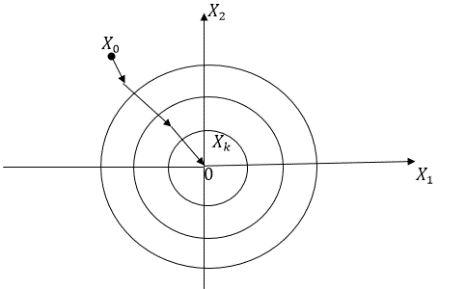
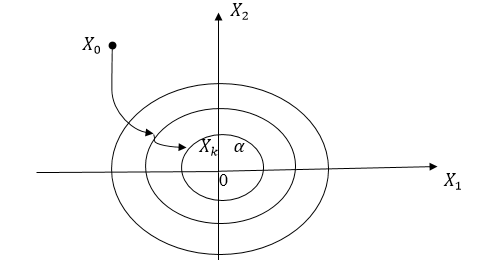
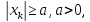 где
Хк
–
конечное значение; которое на доходит
до начала координат.
где
Хк
–
конечное значение; которое на доходит
до начала координат.
Теорема
3. Если
для системы (1.2.9.a)
в
области Д существует
знакоопределенная
положительная функция V(x),
полная
производная которой по времени
 , взятая
в силу системы
(1.2.9.a)
в некоторой части области Д,содержащей
в себе начало координат; совпадает по
знаку со знаком функции V(x),
то
невозмущенное движение х=0
устойчиво
по Ляпунову.
, взятая
в силу системы
(1.2.9.a)
в некоторой части области Д,содержащей
в себе начало координат; совпадает по
знаку со знаком функции V(x),
то
невозмущенное движение х=0
устойчиво
по Ляпунову.
Если
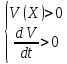 то
невозмущенное
движение
неустойчиво
по Ляпунову.
то
невозмущенное
движение
неустойчиво
по Ляпунову.