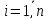6. Получить систему линеаризованных уравнений состояния обьекта в пространстве состояний при малых отклонениях

Все процессы (ОУ) в природе нелинейные. Решать задачи анализа и синтеза САУ для нелинейных ОУ достаточно сложно. Поэтому, если это возможно, нелинейные процессы линеаризуют, а затем для решения различных задач используют классический математический аппарат линейных САУ.

Итак пусть нелинейный процесс описывается следующим уравнением

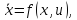(1)

Где x(n*1)- мерный вектор состояния;

u(n*1) -мерный вектор управления;

f(n*1)-мерная вектор-функция.

Нелинейный процесс можно линеаризовать относительно некоторого рабочего состояния, если на вход подать небольшое возмущение

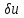
Если на входе процесса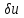, то приращение получат и векторx.f. т. е.

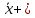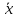
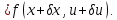δ  (2)

Вычитая уравнения (2) уравнения(1), получим

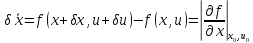
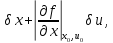
Где 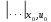означает частная производная в окрестности рабочей точки

Обозначим

A=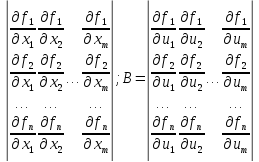

Тогда уравнения(3) перепишется в следующем виде

Которое называется линеаризованным при малых возмущениях.

7.Получить линеаризованные математическое описание динамической системы первого приближения, если нелинейные функции допускают разложение их в степенные сходящиеся ряды.

8. Как определяются собственные числа матрицы? Показать прямой метод определения собственных векторов матрицы.

Если для матрицы А некоторый вектор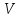удовлетворяет следующему уровнению:

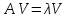, то 𝜆 называется собственным числом матрицы А,(𝜆-скаляр); .

Решим задачу нахождения собственного числа и обственного вектора. Если перенесем переменные в левую часть последего уровнения и вынесем вектор 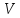вправо, то получим следующее уровнение:

,

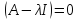где 0-нулевой вектор, т.е. 0=.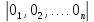

Для того уравнение имело решение, необходимо, чтобы определить матрицы 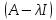был равен нулю,т.е.

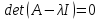
Раскрыть определить, получаем полиномиальное уравнения следующим вида:

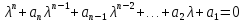(1)

Где 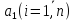–коэффициенты характеристического полинома.

Полученное уравнение 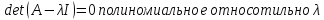и называется характеристическим уравнением матрицыА. Корни характеристического полинома (1)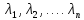называется собственными значениями (собственными числами)матрицы А.

Прямой определение собственных векторов

Пусть имеем линейное однородное уравнение

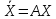
Заданы начальные условия Х(0) =Х₀ ≠ 0.

Решение имеет вид

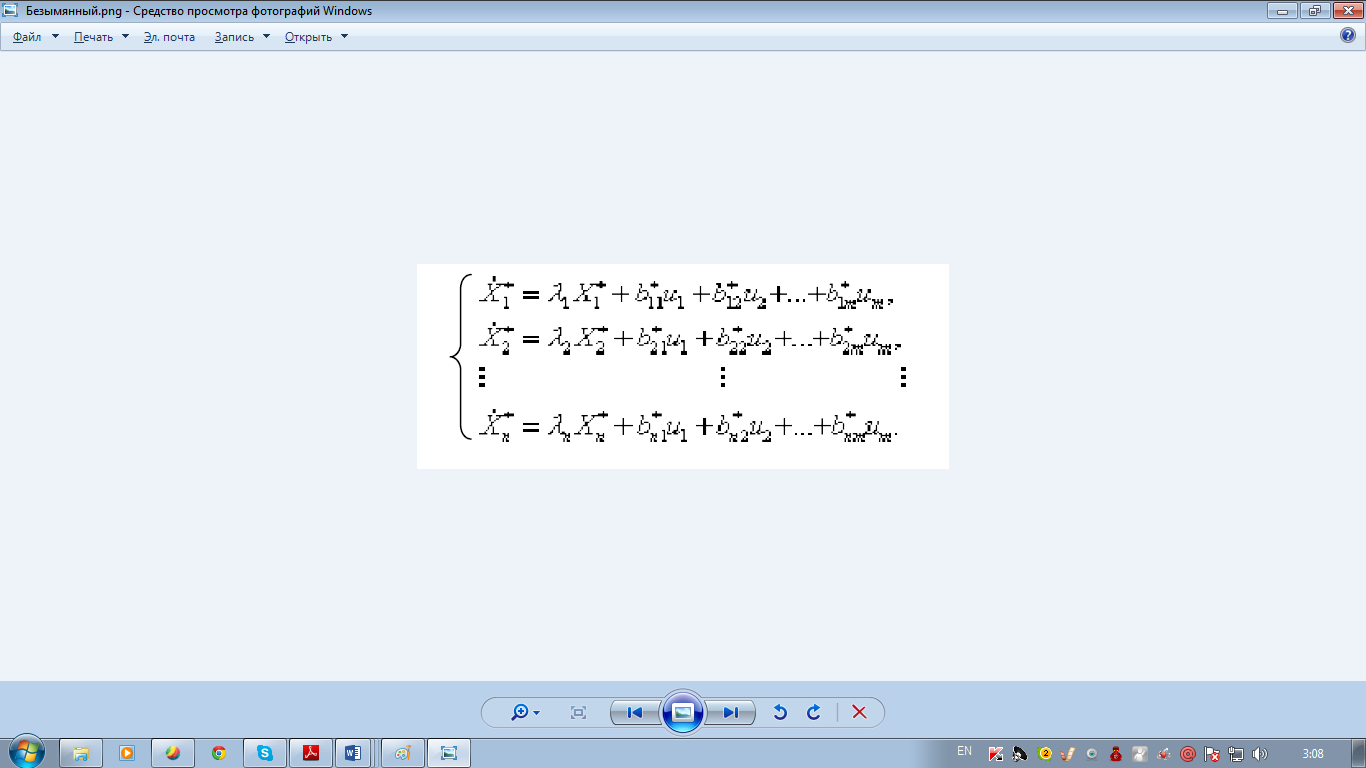
(1.1.17 или в векторной форме

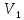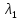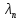Х (t) = V exp(𝜆t) = exp(t) + ... +V_n exp(t),

где v_ij – собственные векторы (i, j =), V_i – вектор стол^бец .

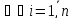Это так называемое каноническое преобразование, в кото- ром матрицей линейного преобразования является матрица собственных векторов V. Возвращаясь к дифференциальному уравнению (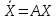),можем записать

^=АV exp(t)=А[V₁ exp(₁t) + ... + V_n exp(_nt)] .. (1.1.18) Дифференцирование уравнения (1.1.17) по t дает

= ₁ V₁ exp(₁t) + … + _n V_n exp(_nt)

Так как левые части уравнений (1.1.16) и (1.1.18) равны, то и правые должны быть равны. Отсюда находим, что собственные векторы V_i удовлетворяют (для случая, когда все _i различны) следующему соотношению: _iV_i exp(_it) = АV_i exp(_it).

Поделив обе части уравнения на exp(_it) ≠ 0,получим _iV_i = АV_i или (A - _iI)V_i=0 (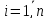.) (1.1.19)

Следовательно, собственные векторы V_i (соответствующие собственным значениям 𝜆_i) можно определить из уравнения (1.1.19). Если матрица А имеет "n" различных собственных зна^{чений, то собственные векторы} V_i ^{являются линейно независи}мыми. Так как матрица А 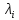I) системы (1.1.13) имеет ранг, который не превосходит величины (n-1), то каждый из собственных векторов V_i определяется с точностью до произвольно^{го множителя}