
- •Линейные преобразования, линейный оператор
- •Линейное преобразование
- •Замечания:
- •Пример 1.3
- •Решение
- •Пример 1.5
- •Пример 1.6
- •Нулевое преобразование:
- •Теорема 1.7: (Свойства линейного преобразования)
- •2.Матричное преобразование
- •Пример 2.2
- •• Пример 2.3. Поворот на плоскости
- •3. Матрица линейного оператора
- •Матрица линейного оператора
- •Матрица линейного оператора
- •4. Подобные матрицы
- •4. Подобные матрицы
- •Теорема 4.3: (Свойства подобных матриц) Пусть матрицы S и T подобны, тогда
Линейные преобразования, линейный оператор
1. Линейные преобразования, линейный оператор 2.Матричное преобразование 3.Матрица линейного оператора 4.Подобные матрицы

Линейное преобразование
Определение 1.1
Пусть U и V - векторные пространства.
Преобразование : U → V есть отображение, которое каждому вектору u из U ставит в соответствие уникальный вектор v из V.
Определение 1.2
Пусть U и V - векторные пространства. Пусть u и v - векторы из U пусть c - скаляр.
Говорят, что преобразование 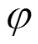 : U → V является
: U → V является
линейным, если
 (u + v) =
(u + v) =  (u) + (v) и
(u) + (v) и  (cu) = c
(cu) = c  (u).
(u).


Замечания:
(1)Говорят, что линейный оператор сохраняет операции.
(cu) c (u)
|
|
|
|
|
Сложение |
|
Сложение |
||
в U |
|
в V |
||
|
|
|
|
|
|
|
|
|
|
Скалярное |
|
Скалярное |
||
умножение в |
|
умножение в |
||
U |
|
|
V |
|
(2)Линейное преобразование :V V векторного пространства в себя называется линейным оператором.

Пример 1.3
Доказать, что следующее преобразование  :R2 → R2 линейно.
:R2 → R2 линейно.
(x, y) = (x y, 3x)
Решение:
“+”: Возьмем (x1, y1) и (x2, y2) R2. Тогда, по определению,  ((x1, y1) + (x2, y2)) =
((x1, y1) + (x2, y2)) = (x1 + x2, y1 + y2)
(x1 + x2, y1 + y2)
=(x1 + x2 y1 y2, 3x1 + 3x2)
=(x1 y1, 3x1) + (x2 y2, 3x2)
“ ”: Пусть c - скаляр. = (x1, y1) + (x2, y2) (c(x1, y1)) = (cx1, c y1) = (cx1 cx2, 3cx1)
=c (x1 y1, 3x1)
=c  (x1, y1)
(x1, y1)
–линейное преобразование.

Решение
Пример 1.4
Показать, что следующее преобразование T: R3 → R2 не является линейным.
 (x, y, z) = (xy, z)
(x, y, z) = (xy, z)
“+”: Возьмем (x1, y1, z1) и (x2, y2, z2) R3. Тогда
 ((x1, y1, z1) + (x2, y2, z2)) = (x1 + x2 , y1 + y2 , z1 + z2)
((x1, y1, z1) + (x2, y2, z2)) = (x1 + x2 , y1 + y2 , z1 + z2)
=((x1 + x2)(y1 y2), z1 + z2)
И (x1, y1, z1) + (x2, y2, z2) = (x1y1, z1) + (x2y2, z2)
(x1, y1, z1) + (x2, y2, z2) = (x1y1, z1) + (x2y2, z2)
Поэтому
 ((x1, y1, z1) + (x2, y2, z2))
((x1, y1, z1) + (x2, y2, z2))  (x1, y1, z1) +
(x1, y1, z1) + (x2, y2, z2).
(x2, y2, z2). 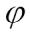 не является линейным преобразованием.
не является линейным преобразованием.

Пример 1.5
Пусть Pn – векторное пространство действительных
многочленов степени n. Показать, что следующее преобразование  : P2 → P1 является линейным.
: P2 → P1 является линейным.
 (ax2 + bx + c) = (a + b)x + c
(ax2 + bx + c) = (a + b)x + c
Решение |
|
|
“+”: Возьмем |
ax2 bx c и px2 qx r |
P . Тогда |
|
|
2 |
((ax2 bx c) ( px2 qx r)) ((a p)x2 (b q)x (c r))(a p b q)x (c r) (a b)x c ( p q)x r
(ax2 bx c) ( px2 qx r)
“ ”: Пусть k – произвольный скаляр.
(k(ax2 bx c)) (kax2 kbx kc) k((a c)x c)k (ax2 bx c)

Пример 1.6
Обозначим через D оператор дифференцирования для действительных многочленов (D есть то же самое, что и
D можно интерпретировать как отображение Pn в себя.
Например,
D(4x3 3x2 2x 1) 12x2 6x 2
dxd .)
Пусть f , g Pn а c - скаляр. Следующие свойства производной показывают, что D есть линейный оператор.
D(f + g) = Df + Dg
D(cf) = cD(f)
Нулевое преобразование:
:U V |
(u) 0, 0 V , u V |
Единичный оператор:
:V V |
(v) v, v V |

Теорема 1.7: (Свойства линейного преобразования)
(1)(0) 0
(2)( v) (v)
(3)(u v) (u) (v)
(4)(c1v1 c2 v2 ck vk ) c1 (v1) c2 (v2 ) ck (vk )
Доказательство.
(1) |
Пусть v – произвольный вектор из V. |
||
|
(0)= (0v) = 0 (v) = 0 |
|
|
(2) |
(-v) = |
((-1)v) = (-1) |
(v)= - (v) |
(3) |
(u-v)= |
(u + (-1)v) = |
(u) + (-1) (v) = (u) - (v) |
k |
k |
(4) (c1v1 c2 v2 ck vk ) ( ci vi ) (ci vi ) |
|
i 1 |
i 1 |
(c1v1) (c2 v2 ) (ck vk ) c1 (v1) c2 (v2 ) ck (vk )
