Свойства последовательного и параллельного колебательных контуров
Последовательный контур
XL > XC
UC
E UL
Схема последовательного контура |
UR |
|
X,R |
||
Комплексное сопротивление |
||
|
модуль
0 - резонансная частота контура На 0 UR=E; UL=j 0LI; UC=-jI/ 0C
Частотные характеристики сопротивлений реактивных элементов и модуля комп- лексного сопротивления
Обычно потери в контуре
Характеристическое сопротивление контура -
Добротность контура -
Часто комплексное сопротивление контура выражают через 0 и Q.
обобщенная расстройка (кси)
- 0
расстройка
-
АЧХ и ФЧХ посл. контура
-абсолютная
-относительная
расстройка
- обобщенная расстройка
относительная
полоса
пропускания
ФЧХ
Реактивное сопротивление последовательного контура XK( )
на частоте < 0 имеет емкостной характер (XL<XC, ХК<0, I опережает U), на частоте > 0 - индуктивный (XL>XC, ХК>0, I отстает от U).
Относительная полоса пропускания резонансной характеристики по уровню 0,707 от максимума обратно пропорциональна добротности, фазовый сдвиг тока в контуре на границах полосы пропускания равен /4.
Дифференцируя, получим
R |
1 |
|
введем |
|
i'' L i' |
LC i 0 |
|||
|
||||
Начальные условия
Общее решение в виде
Корни характер. уравнения
uR + uL + uC = e(t)
uR=Ri, uL=Ldi/dt, i=CduC/dt
L |
di |
iR |
1 |
t |
i( t')dt' u |
( 0) E |
|
|
|
||||
|
C 0 |
|||||
|
dt |
|
C |
|
||
|
|
|
|
|||
R / 2L |
i'' 2 i' 2i 0 |
||||
|
|
|
0 |
||
2 |
1 /( LC ) |
|
|
|
|
0 |
|
|
|
|
|
uC(0)=0, |
i( 0) 0 , |
i' |
|
t 0 ( 1 / L ) E |
|
|
|||||
|
|||||
i A e 1t A e 2t |
|
|
|
||
|
1 |
2 |
|
|
|
2 |
2 2 |
0 |
|||
|
|
0 |
|
|
|
|
, |
2 2 |
1 ,2 |
|
0 |
при 0 |
i(t) |
E |
e t sin( кt) |
|
||
|
|
|||||
|
|
|
к L |
|
|
|
|
k |
2 |
2 1 ( 1 / 2Q ) 2 |
|
||
|
0 |
0 |
|
0 |
||
Период и частота собственных затухающих колебаний контура
T=2 / к, fк=1/T
Скорость затухания определяют логарифмическим декрементом затухания
=ln(Un/Un+1)= T= 2 / к= Q
Переходные характеристики напряжений на C и L последовательного контура
Измерение частоты собств. колебаний 0 и добротности Q последовательного контура
=ln(Un/Un+1)= T= 2 / к= /Q
Параллельный колебательный контур
Для контура без потерь проводимость |
YK=jBK=j(BL+BC)=j( C-1/ L) |
||
Комплексное сопротивление |
Z =1/Y =- j/B =- j L/( CL- |
||
1) |
K |
K |
K |
|
|
|
|
Комплексное сопротивление контура с учетом его потерь
| R<< L
Схема параллельного контура
| :C/:C 0 - резонансная частота контура
= L= 1/ C - характеристическое
сопротивление контура
Q= /R – добротность контура
0 0 - относительная расстройка
2Q – обобщенная расстройка
- эквивалентное сопротивление
контура
ЧХ и ФЧХ комплексного сопротивления параллельного контура
- модуль комплексного сопротивления контура
- аргумент модуля сопротивления
- вещественная и мнимая части комплексного сопротивления контура
2 |
|
Â Í |
Â Í |
|
|
1 |
- относительная |
|
0 |
0 |
Q |
||||||
|
|
|
полоса |
|||||
|
|
|
|
|
|
|
пропускания |
|
Реактивное сопротивление параллельного контура ХК( )
при < 0 - индуктивный характер (ХК>0), при > 0 - емкостной (ХК<0) .
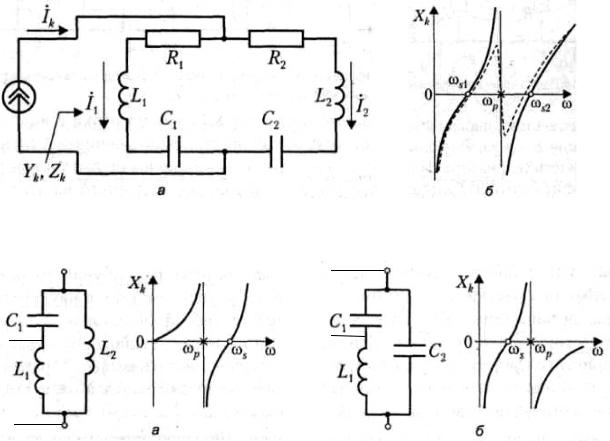
Сложный колебательный контур общего вида (а) и частотная характеристика реактивного сопротивления сложного контура (б)
Коэф. вкл. конт.
р=L1/(L1+L2)
Rэкв1= p2 |
р=Ск/С1 |
|
|
С =С С /(С С |
) |
||
|
Rэкв1к =1p22 |
1 2 |
|
Сложные контуры второго (а) и третьего (б) видов и частотные характеристики реактивных сопротивлений этих цепей
Сложные контуры позволяют в ограниченной полосе частот, примыкающей к частоте параллельного резонанса, трансформировать значения сопротивлений.
Поэтому их применяют для согласования сопротивлений источника и нагрузки, когда требуется реализовать режим передачи потребителю максимальной мощности от источника.
0 |
|
|
1 |
|
|
, |
|
f0 |
|
|
|
|
1 |
|
|
|
|
- резонансная частота контура |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
LC |
|
|
2 |
LC |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= L= 1/ C |
= |
|
|
L |
|
|
|
|
|
– характеристическое сопротивление контура |
||||||||||||||||
|
|
C |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Q |
|
|
L |
|
1 |
|
|
|
|
|
|
|
|
|
|
– добротность, r – сопротивление потерь контура |
||||||||||
r |
Cr |
|
|
|
|
|
||||||||||||||||||||
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Rэкв Q LQ |
|
Q |
|
|
L |
Q2r |
|
2 |
- эквивалентное сопротивление |
|||||||||||||||||
C |
Cr |
|
r |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
параллельного контура |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Реактивное сопротивление последовательного контура XK( )
на частоте < 0 имеет емкостной характер (XL<XC, ХК<0, I опережает U), на частоте > 0 - индуктивный (XL>XC, ХК>0, I отстает от U).
Реактивное сопротивление параллельного контура ХК( ) при < 0 - индуктивный характер (ХК>0), при > 0 - емкостной (ХК<0) .