
Алгебра 2
.pdf
№1. Найти базис линейной оболочки строк матрицы A
№2. Найти базис пространства решений системы Ax=0

№3.
Даны столбцы e1 , e2, e3, f1, f2, f3, x .
А). Найти матрицы перехода C ( e-> f ) и C (f -> e)
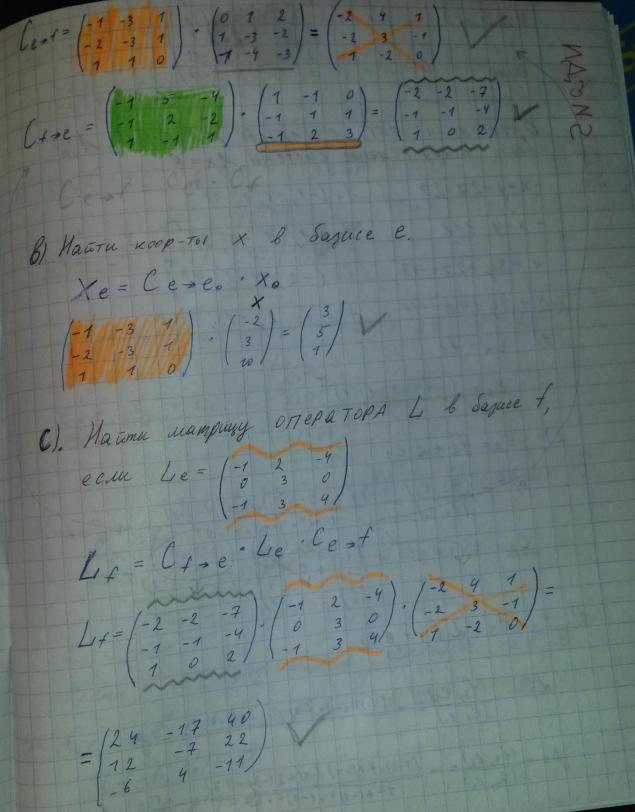
В). Найдите координаты x в базисе e .
С). Найдите матрицу оператора L в базисе f , если Le = (какая то дана матрица)
L

№4.
Даны A = (…) b= (…)
Ортогонализовать столбцы матрицы A и найдите псевдорешение системы Ax=b



№5.
Запишите столбец координат элемента (матрица какая то) в базисе e1 , e2 , e3, e4 .
№6.
Является ли набор векторов e1 , e2 , e3 , e4 линейно независимым и / или системой образующих в R^3 ?

№7.
Найдите координаты столбца x = (…) в базисе f1 , f2 , f3 .

№8.
Найдите координаты столбца x = (..) в ортогональном базисе f1 , f2 , f3

№9.
Являются ли ортогональными многочлены x и 3x-4 относительно скалярного произведения ( f,g )= интеграл …
№10.
Являются ли набор векторов e1 , e2 , e3 базисом в R^3 ?
