Поправки за наклон линий

Угол наклона	Длина линии, м
	10	20	30	40	50	60	70	80	90	100
	Поправка, мм
2°00¢	6	12	18	24	30	37	43	49	55	61
2°30¢	10	19	29	38	48	57	67	76	86	95
3°00¢	14	27	41	55	69	82	96	110	123	137
3°30¢	19	37	56	75	93	112	131	149	168	187
4°00¢	24	49	73	97	122	146	171	195	219	244
4°30¢	31	62	92	123	154	185	216	247	277	308
5°00¢	38	76	114	152	190	229	266	304	342	381

По завершении вычислений в журнале теодолитного хода вычерчивается схема этого хода (рис. 1.59), на которой приводятся средние значения горизонтальных углов, проложений линий, заданный дирекционный угол линии 1 -2.

Для определения координат вершин теодолитного хода разрабатывается ведомость координат (табл. 1.6). Эти координаты получают путем последовательного решения прямой геодезической задачи, исходя из известных (заданных по табл. 1.3) координат X₁и Y₂вершины угла 1, дирекционного угла линии 1-2 и полученных после обработки журнала теодолитного хода средних значений горизонтальных углов и длин линий хода. При этом должен обеспечиваться контроль вычислений во всех необходимых случаях.

Последовательность разработки ведомости координат следующая.

1. Вписать в графу 1 ведомости со схемы теодолитного хода номера углов, начиная и заканчивая номером 1 (теодолитный ход сомкнутый).

2. Вписать из журнала теодолитного хода в графу 2 средние значения горизонтальных углов, в нижней части ведомости указать полученную угловую невязку . Распределить эту навязку (с обратным знаком), зафиксировать это распределение в графе 3.

3. Вычислить исправленные значения горизонтальных углов (графа 4). В графы 2 и 4 величину угла 1 вписывать один раз, только в первой строке.

Т а б л и ц а 1.6

Ведомость вычисления координат вершин теодолитного хода

Номер угла

Измеренный угол

Поправка к углу

Исправленный угол

Дирекционный угол

Румб

Длина линии d

Приращения вычисленные

Поправки к приращениям

Приращения исправленные

Координаты

название

величина



x



y



x



y



x



y



X



Y

1

2

3

4

5

6

1

Угловая невязка

Невязка хода

Допустимая невязка

Относительная невязка

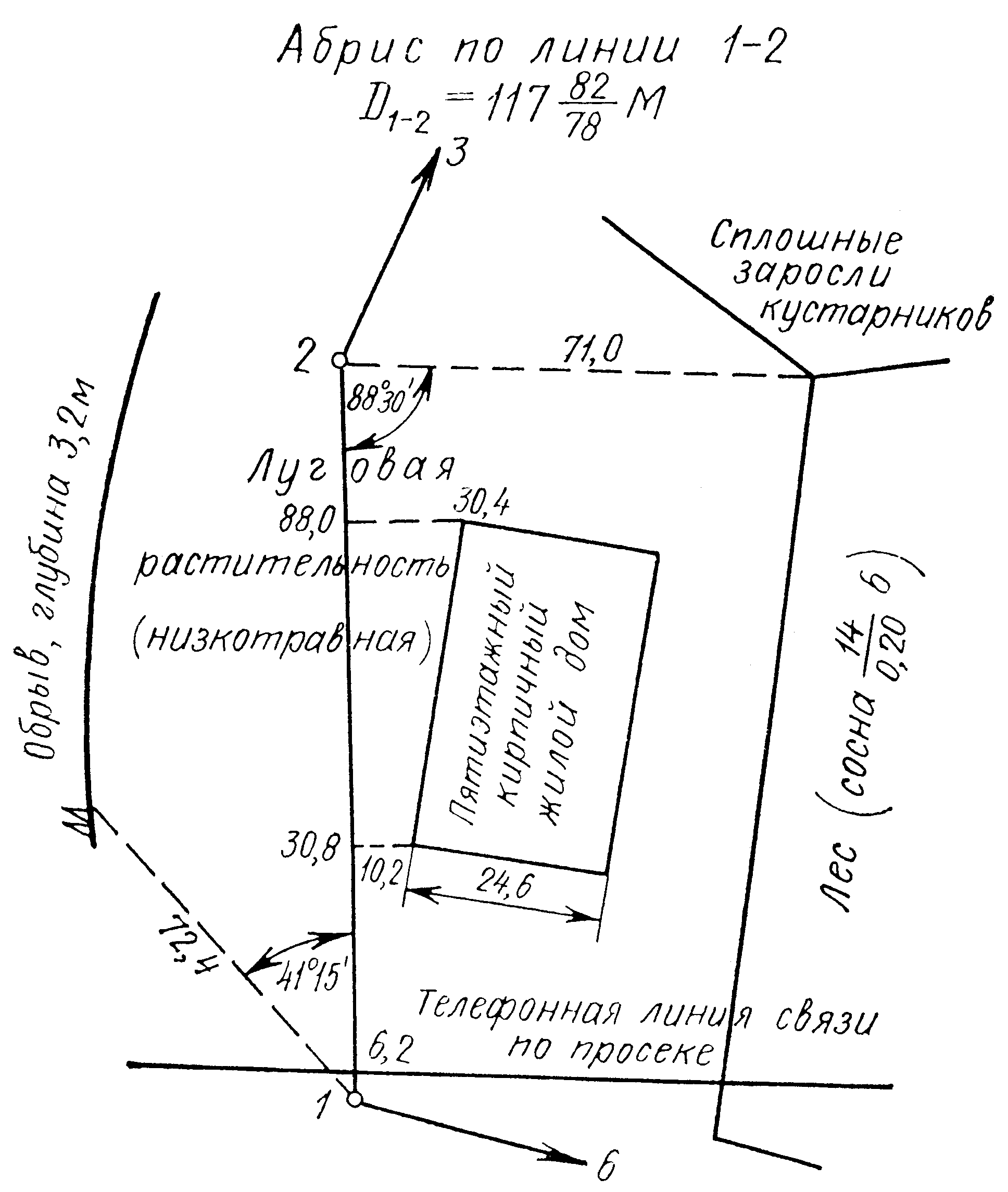
Рис. 1.53. Абрис по линии 1–2	Рис. 1.54. Абрис по линии 2–3
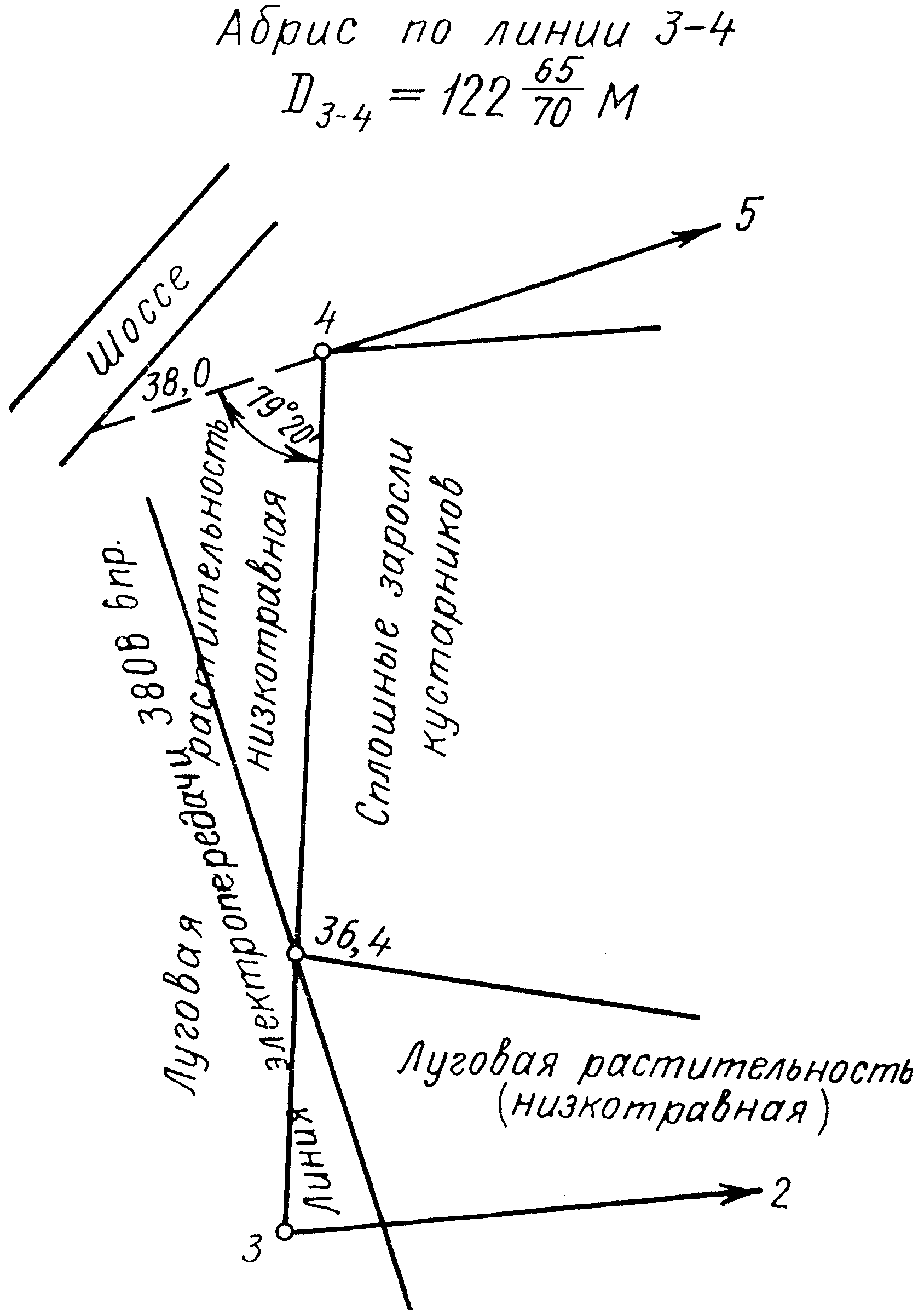
Рис. 1.55. Абрис по линии 3–4	Рис. 1.56. Абрис по линии 4–5
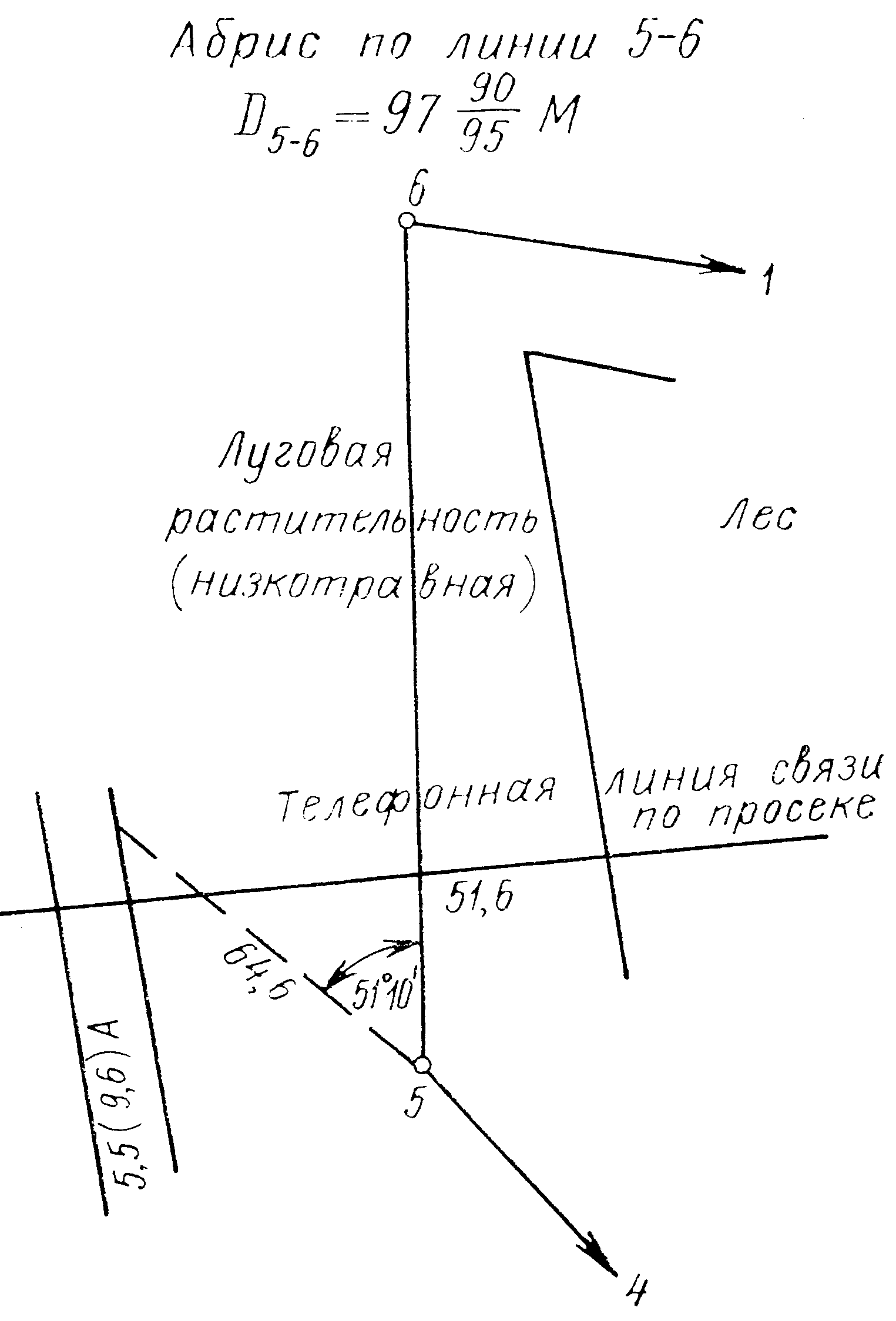
Рис. 1.57. Абрис по линии 5–6	Рис. 1.58. Абрис по линии 6–1

Вычислить сумму исправленных углов -она должна быть равна теоретической сумме внутренних углов полигона, в данном случае= 180°(n -2) = 180°(6-2) = 720°.

4. В графу 5 вписать заданный дирекционный угол линии 1 -2. Так как дирекционный угол относится к линии между соответствующими вершинами хода, то и вписывать его следует в строку, расположенную между этими вершинами.

По заданному дирекционному углу исходной линии 1 -2 и исправленному внутреннему углу полигонавычислить дирекционный угол линии 2-3:

. (1.12.1)

Вычислить последовательно дирекционные углы всех линий полигона (в необходимых случаях прибавляя или вычитая 360°00¢). Контролем правильности вычисления дирекционных углов сторон сомкнутого хода является вторичное получение дирекционного угла исходной стороны.

По известным дирекционным углам определить румбы (графы 6, 7), знаки приращений координат (графы 9, 11).

5. Вписать в графу 8 длины линий и вычислить приращения координат: ,.

При вычислении приращений используют таблицы натуральных значений тригонометрических функций или таблицы приращений координат.

Вычисленные приращения координат, округленные до сотых долей метра, заносят в графы 10 и 12, определяют невязки и, абсолютную невязку в периметре, относительную невязку, которая не должна превосходить допустимую невязку (в данной работе 1:2000).

Невязки ираспределяют пропорционально длинам сторон, поправки фиксируют в графах 13, 14, 15, 16, вычисляют исправленные приращения координат. Контролем служит равенство сумм исправленных приращений со знаком «плюс» и «минус».

6. Вписать в графы 21 -24 заданные координаты вершины угла 1, вычислить координаты всех других вершин полигона:

; .(1.12.2)

Контролем правильности вычислений является получение в конце расчета заданных координат угла 1. При выполнении данного условия разработка ведомости координат заканчивается.

Для вычерчивания плана на листе чертежной бумаги размерами А4 (см. рис. 1.52) обозначаются рамка, штамп, таблица координат вершин углов полигона, строится сетка координат с размерами квадратов 50 ´ 50 мм.Графическая точность построения сетки контролируется по сторонам квадратов, по сумме четырех сторон, по диагоналям основного квадрата.

Под сеткой квадратов выписать масштаб плана (1:2000).

После построения сетки квадратов наносят по координатам вершины углов полигона. Для этого необходимо выбрать начало координат так, чтобы участок местности, подлежащий отображению на плане, разместился в пределах сетки квадратов. Для этого из таблицы координат выбирают наибольшие и наименьшие значения координат (,,,) и, ориентируясь по схеме полигона (см. рис. 1.59), назначают целесообразные координаты начальной точки сетки координат с округлением координат до десятков метров. Сетка координат оцифровывается применительно к масштабу плана (1:2000).

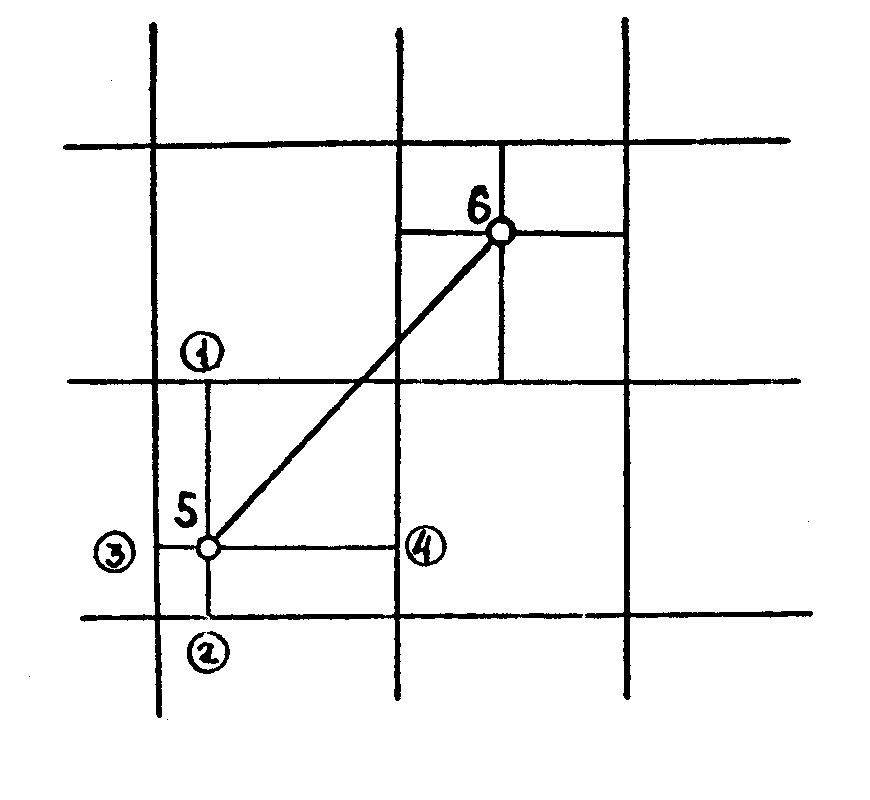
Рис. 1.59. Схема теодолитного полигона	Рис. 1.60. Схема нанесения вершин теодолитного хода на координатную сетку

Для нанесения вершин теодолитного хода определяют квадрат сетки, в котором эта вершина находится, при помощи циркуля-измерителя и поперечного масштаба откладывают по сторонам квадрата (рис. 1.60) значения разностей координат данной вершины угла и соответствующей линии координатной сетки (точки 1 и 2, 3 и 4). Соединив точки 1 и 2, 3 и 4 получают в пересечении отрезков искомую вершину полигона (например, вершину угла 5). В этой точке иглой циркуля делают накол и вычерчивают условный знак точки плановой съемочной сети. Для каждой пары точек определяют расстояние между ними и сравнивают его с приведенным на схеме полигона (см. рис. 1.59) - расхождение не должно превышать 0,3 мм (в масштабе плана).

Построение контуров местности на плане производят по абрисам (см. рис. 1.53 -1.58). Способ вычерчивания контуров определяется способом съемки, при этом применяют геодезический транспортир, поперечный масштаб, линейку и выверенный прямоугольный треугольник.

Все построения выполняют предельно тонкими линиями, так как часть этих линий при последующей разработке плана будет заменяться на точечный пунктир, линии вспомогательных построений должны быть убраны. Значения углов и длин линий, приведенные в абрисах, на план не выписывают.

После вычерчивания контуров оформление плана производится в точном соответствии с обязательными условными знаками, т.е. на план наносят в карандаше условные знаки с соблюдением их размеров и начертания согласно действующим «Условным знакам для планов масштаба 1:5000; 1:2000; 1:1000; 1:500».