2. Прочность грунтов при сложном напряженном состоянии.

Изотропные грунты

Для сред и материалов, обладающих сплошностью, предложены различные условия прочности. Для оценки прочности изотропных грунтов наиболее широкое распространение получило условие Кулона – Мора (3.19), не содержащее промежуточного главного напряжения σ₂ и тем самым отрицающее влияние σ₂ на прочность грунта. Реже применяется условие Хилла – Треска

σ₁ – σ₃ = (σ₁+ σ₃)tgφ₄₅⁰ + 2c₄₅⁰,

которое, как и условие Кулона-Мора, не учитывает σ₂. Это условие исходит из предположения разрушения грунта путем сдвига по площадкам, которые параллельны σ₂ и наклонены к направлению σ₁ под углом 45⁰ (для условия Кулона-Мора – под углом 45⁰ - φ/2 (см. разд. 3.8). В условии Хилла-Треска φ₄₅⁰, c₄₅⁰ – параметры прочности грунта в соответствии с данным условием.

Через инварианты σ_cp, Т и μ_σ условие Кулона-Мора получает [3,10] вид:

.

Другим, используемым на практике для грунтов, условием прочности является предложенное А.И. Боткиным условие, которое предполагает, что на прочность грунта влияют все три главных напряжения, а предельное состояние наступает на октаэдрической площадке. Условие Боткина можно также записать аналогично условию Кулона-Мора в виде

с_окт ctg ρ_окт = 0,

где ρ_окт, с_окт – параметры прочности грунта на октаэдрической площадке.

Поскольку условия Кулона-Мора и Боткина по-разному оценивают влияние σ₂ на прочность грунта, теоретическое сопоставление этих условий позволяет прогнозировать возможный характер изменения характеристик прочности в зависимости от вида напряженного состояния. Приравнивая коэффициенты при Т и свободные члены условий Кулона-Мора и Боткина, получаем

tg ρ_окт = ,

(8.10)

с_окт ctg ρ_окт = c ctgφ .

Из анализа соотношений (8.10) следует, что если бы разрушение грунтов в полной мере отвечало условию Кулона-Мора, то φ и с должны были бы получаться одними и теми же независимо от созданных в опытах комбинаций главных напряжений, т.е. независимо от параметра μ_σ (рис. 8.8, прямые 2). Как следует из соотношений (8.10), автоматически это означало бы получение в опытах с различными μ_σ различных значений ρ_окт и с_окт. И наоборот, если бы разрушение грунтов в точности описывалось условием Боткина, то это означало бы постоянство ρ_окт и с_окт и одновременно переменность φ (кривые 3) и с при изменении значений μ_σ. Чем меньше абсолютное значение угла внутреннего трения (φ₀ на рис. 8.8), тем меньше на его изменение влияет μ_σ.

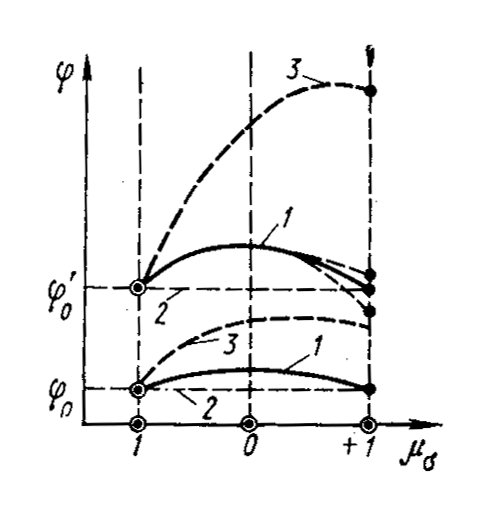
Рис. 8.8. Характер зависимости угла внутреннего трения φ

(по Кулону – Мору) от параметра Лоде μ_σ:

1 – по данным опытов; 2 – по Кулону – Мору; 3 – по Мизесу – Боткину.

Выполненные эксперименты, в основном, на приборах с независимо изменяемыми главными напряжениями показали, что в сыпучих грунтах наблюдается изменение угла внутреннего трения φ условия Кулона-Мора в зависимости от изменения промежуточного главного напряжения или, что то же самое, в зависимости от μ_σ (рис. 8.8, кривые 1). Для песчаных грунтов получены изменения величины φ в одних опытах, например, от 35⁰ при μ_σ = -1 до 48⁰ при μ_σ = 0 и 44⁰ при μ_σ = +1, в других опытах изменение φ было много меньшим: от φ = 39⁰ при μ_σ = -1 до 42⁰ при μ_σ = 0 и φ = 39⁰ при μ_σ = +1. Однако в опытах это изменение было не столь большим, как это следует из теории прочности Боткина (кривые 3). Таким образом, опыты с песками при сложном напряженном состоянии не подтвердили точного выполнения теории прочности Кулона-Мора и Боткина. В связи с этим в последние годы были предложены новые уточненные условия прочности, как правило, весьма сложные и неудобные для практического применения. Вместе с тем — и это наиболее существенно — было показано (М.В. Малышев [10]), что расчеты грунтовых массивов могут основываться на условии Кулона-Мора и давать достоверные результаты, если в этом условии принимается угол внутреннего трения φ, отвечающий тому значению параметра μ_σ, которое будет в данном массиве в натуре.

В частности, при расчетах массивов, нагружаемых в условиях плоской деформации, следует принимать φ при том значении параметра Лоде μ_σ, которое наблюдается при плоской деформации. Если определение характеристик прочности выполнено не при том значении μ_σ, при котором производится расчет (например, определение характеристик прочности производится на стабилометре, а расчет будет выполняться для условий плоской деформации), то требуется произвести их пересчет применительно к плоской деформации, используя для этого пересчета имеющиеся в литературе рекомендации.

Обоснование возможности использования условия Кулона-Мора при любом виде напряженного состояния с соответствующим при необходимости пересчетом характеристик прочности сняло вопрос о необходимости перестроения теории предельного равновесия и переработки ее решений, что явилось значительным достижением.

Приведенные выше условия прочности (предельного напряженного состояния) базируются на концепции разрушения грунта в форме сдвига, даже при одноосном сжатии или растяжении образца. При этом основой, объединяющей различные условия прочности, является представление о проявлении на площадках сдвига закона трения; различие же между ними определяется принимаемым положением площадок скольжения в пространстве. В частности, условия Кулона-Мора и Хилла-Треска, не содержащие напряжения σ₂, постулируют площадки сдвига всегда параллельными направлению σ₂, а условие Боткина предполагает наступление предельного состояния на площадке, которая одинаково наклонена к напряжениям σ₁, σ₂, σ₃. Заметим, что для грунтовых массивов, находящихся в условиях плоской деформации, возможная реализация сдвигов только в плоскости σ₁, σ₃, предопределяет использование в расчетах условий, не содержащих σ₂. Применение условия Боткина в этом случае может приводить к ошибкам.

Сдвиговой механизм разрушения грунта хорошо подтверждается экспериментами, если в образце нормальные напряжения по потенциальным площадкам сдвига являются сжимающими. Для этого случая на различных приборах трехосного сжатия (стабилометры и приборы с независимыми главными напряжениями) для многих грунтов детально изучен характер огибающей предельных кругов напряжений. В последние годы для выявления характера огибающей в области растягивающих напряжений ( < 0) был выполнен целый ряд экспериментальных исследований, в которых создавалось одноосное, реже двухосное и трехосное напряженные состояния. По результатам опытов огибающая к предельным кругам напряжений в области растягивающих и малых сжимающих напряжений  получена существенно нелинейной, а предельное состояние вместо уравнения (2.8) удовлетворительно аппроксимируется зависимостью вида

 = ₀ ,

где ₀,  — экспериментально определяемые параметры; , с — параметры условия прочности (2.8), с которым стыкуется нелинейное условие прочности. Применение вместо нелинейного линейного условия прочности Кулона-Мора в области  < 0, что нередко еще практикуется при расчетах, приводит к значительному завышению прочности при растяжении по сравнению с экспериментальными значениями. Это обстоятельство следует учитывать при использовании Кулона-Мора в расчетах грунтовых сооружений и оснований из связных грунтов при появлении в них растяжения.

Анизотропные грунты.

Ранее, в разд. 2.3, отмечалось, что у многих грунтов наблюдается проявление прочностной анизотропии, представленной обычно вариантом трансверсальной изотропии [3]. Опыты на сдвиговых приборах показали, что соотношение между касательным и нормальным напряжениями по заданной площадке разрушения подчиняется зависимости Кулона

_ = _{ ·} tg_ + с_ , (8.11)

в которой tg_, с_ - параметры прочности на площадке разрушения, наклоненной к плоскости изотропии под углом .

Представление условия Кулона в главных напряжениях в случае анизотропного грунта является более сложным, чем для изотропного грунта. При анализе напряженного состояния элемента (образца) грунта, ограниченного главными площадками, полагаем направление напряжения ₃ совпадающим с плоскостью изотропии. В этом случае угол  в (8.11) отсчитывается от направления ₃. Если в уравнении (8.11) выразить _ и _ через главные напряжения по известным соотношениям

_ = , _ = ,

то уравнение предельного равновесия (8.11) примет вид

₁ - ₃ = (₁ + ₃) + . (8.11^/)

В случае изотропного грунта наклон площадки скольжения к направлению ₃ всегда  = _пр = 45⁰ + /2 и (8.11^/) принимает известный вид уравнения (3.19). Для определения положения площадок скольжения в случае анизотропного грунта уравнение (8.11^/) при известных ₁, ₃ должно решаться совместно с соотношениями, принимаемыми по данным экспериментов [3] в виде:

tg _ = tg₁ + (tg₂ – tg₁ ) sin²,

c_ = c₁+ (c₂ – c₁) sin²,

где tg₁, c₁ – характеристики прочности при сдвиге по направлению слоистости (вдоль плоскости изотропии), а tg₂, c₂ – то же при сдвиге поперек слоистости (поперек плоскости изотропии).

Как показывает анализ, положение площадки предельного равновесия, т.е. _пр, в общем случае зависит от напряженного состояния (₁, ₃) и соотношения характеристик прочности вдоль и поперек плоскости изотропии (с₂/с₁, tg₂/tg₁). В частном случае с₂/с₁ = tg₂/tg₁ угол _пр оказывается независящим от ₁/₃ . Например, в случае анизотропного суглинка с горизонтальной плоскостью изотропии при с₂/с₁ = tg₂/tg₁ = 1,5 и значениях ₁ = 21⁰, c₁ = 0,02 МПа (направление 1 – вдоль плоскости изотропии) площадка разрушения при раздавливании образца в стабилометре будет наклонена к горизонту (к направлению ₃) под углом _пр = 54⁰. Значения характеристик прочности на площадке разрушения составляют _ = 26,5⁰, c_ = 0,0265 МПа.

В общем случае несовпадения направлений ₃ и плоскости изотропии угол между ними будет входить в уравнение предельного равновесия и анализ разрушения существенно усложняется.