8. Нелинейная деформируемость и прочность грунтов. Основы нелинейной механики грунтов.*)

В настоящее время наблюдается существенный рост объемов промышленно-гражданского строительства, при этом возводятся все более высокие и тяжелые сооружения (АЭС, ТЭС, ГЭС, сооружения на шельфе морей и океанов, жилые комплексы со зданиями большой этажности, объекты спорта и туризма и др.), создающие значительные нагрузки на основания, в составе которых часто присутствуют грунты повышенной деформируемости (средне и сильно сжимаемые) и низкой прочности. При оценке напряженно-деформированного состояния (НДС) таких оснований и величин смещений (осадок, кренов и т.п.) сооружений достоверность расчетных результатов может быть обеспечена только при учете нелинейной деформируемости грунтов, в первую очередь нескальных, развития в основании областей предельного (пластического) состояния, что предполагает применение более сложных, чем линейно-деформируемая среда, нелинейных (упругопластических) моделей грунта. Указанный учет необходим как при новом строительстве, так и проведении больших реконструкционных работ в условиях плотной городской застройки.

1. Нелинейная деформируемость грунтов.

За последние десятилетия в результате многочисленных экспериментальных исследований с применением различных схем испытаний в приборах и установках, реализующих двух- и трехосное напряженно-деформированное состояние грунта, получены обширные данные о нелинейном деформировании грунта при сложном напряженном состоянии (начальные представления об этом – см. главы 2 – 5). Особенности нелинейного деформирования грунта наиболее ярко выявляются при сравнении со свойствами моделей линейной теории упругости и деформационной теории пластичности, широко применяемых в практике расчетов различных конструкций из металла, железобетона, дерева и др.

Модели линейной теории упругости и деформационной теории пластичности.

В линейной теории упругости рассматривается идеально упругая среда со строго линейной зависимостью между напряжениями и деформациями при любом уровне действующей нагрузки. Для общего случая напряженного состояния считается справедливым обобщенный закон Гука (3.5). Из зависимостей (3.5) следуют соотношения, связывающие между собой инварианты напряженного и деформированного состояний в виде

σ_ср = Е·ε_ср/(1-2ν) = К·ε_ср = К·ε_v/3,

(8.1)

Т = Е·Г/[2(1+ν)] = G · Г или σ_i = 3G · ε_i,

где σ_ср = (σ_x + σ_y + σ_z)/3 = (σ₁ + σ₂ + σ₃)/3 – среднее напряжение или всестороннее (гидростатическое) сжатие;

σ_i= = — интенсивность напряжений;

Т = — интенсивность касательных напряжений;

ε_ср = (ε_x + ε_y + ε_z)/3 = (ε₁ + ε₂ + ε₃)/3 — средняя деформация;

ε_v = 3 ε_ср — объемная деформация;

Г =

= — интенсивность деформаций сдвига;

ε_i = · Г – интенсивность деформаций; Г и ε_i характеризуют формоизменение среды.

Подробная характеристика инвариантов σ_ср, σ_i, Т, ε_ср, ε_i Г дана в ([9], раздел 2.4), написанном автором данного пособия.

Линейные соотношения (8.1) констатируют, что в среде линейной теории упругости объемные деформации ε_v = 3 ε_ср вызываются только всесторонним сжатием σ_ср, а изменение формы (Г или ε_i) – девиатором напряжений, характеризуемым σ_i или Т. Помимо соотношений (8.1) из закона Гука следует равенство μ_σ = μ_ε параметров Лоде вида напряженного и деформированного состояний, называемое соотношением подобия этих состояний, и условие совпадения (коаксиальности) главных осей тензоров напряжений и деформаций. Параметры Лоде определяются по зависимостям:

μ_σ = и μ_ε = .

В деформационной теории пластичности рассматривается среда, для которой характерно ярко выраженное нелинейное деформирование с ростом нагрузок. Наиболее близко к свойствам этой среды приближаются конструкционные материалы, в основном, металлы, работающие за пределом упругости (текучести). Появление за пределом упругости пластических (остаточных) деформаций, добавляющихся к упругим, обусловливает нелинейность процесса деформирования при нагружении, которая обеспечивается за счет нелинейности формоизменения.

В деформационной теории пластичности принимается линейная зависимость

σ_ср = Кε_ср (8.2)

для объемной (средней) деформации и нелинейная – между компонентами девиатора напряжений и деформаций:

σ_x – σ_ср = ψ(ε_x – ε_ср),

σ_y – σ_ср = ψ(ε_y – ε_ср),

σ_z – σ_ср = ψ(ε_z – ε_ср),

τ_xy = ψγ_xy, (8.3)

τ_yz = ψγ_yz,

τ_zx = ψγ_zx,

где ψ – скалярная функция инвариантов напряжений и деформаций, подлежащая экспериментальному определению. Подстановка напряжений из выражений (8.3) в формулы для Т или σ_i приводит к зависимостям

Т = ψГ или σ_i = ψ ε_i,

которые для металлов имеют вид Г = Г(Т) или ε_i = ε_i (σ_i), определяя так называемый «закон единой кривой деформирования», согласно которому формоизменение связано только с девиатором напряжений и не зависит от среднего давления σ_ср и параметра Лоде μ_σ. Принимается, что имеет место подобие напряженного и деформированного состояний, т.е. μ_σ = μ_ε , и коаксиальность осей тензоров напряжений и деформаций.

При решении задач плоской деформации, включая упругопластические, удобным оказалось применение инвариантов напряжений

Т_пл = ,

σ_ср.пл. = ,

называемых интенсивностью касательных напряжений и средним давлением при плоской деформации, и инварианта деформаций

Г_пл = (ε₁ – ε₃) = ,

называемого интенсивностью деформаций сдвига при плоской деформации.

Инварианты Т_пл, σ_ср.пл. в точности равны инвариантам Т и σ_ср., если в формулах для Т, σ_ср принять σ₂ = σ_y = 0,5 (σ_x + σ_z). При использовании инвариантов Т_пл, σ_ср.пл условие Кулона (3.19) получает простую запись

Т_пл = σ_ср.пл ∙sinφ + c∙cosφ

и легко геометрически интерпретируется в координатах Т_пл, σ_ср.пл.

Основные особенности деформирования нескальных грунтов.

Как показал анализ экспериментального материала, деформирование нескальных грунтов как дисперсных систем характеризуется более сложными закономерностями, чем поведение расчетных моделей теорий упругости и пластичности. К настоящему времени наиболее полно установлены закономерности изменения полных деформаций изотропных грунтов, т.е. состоящих из упругих и пластических, и на этой основе в рамках деформационной теории пластичности сформулированы общепринятые сейчас в нелинейной механике грунтов представления о деформируемости грунтовой изотропной среды при ее нагружении.

Деформация формы в грунтах является преимущественно пластической и зависит не только от девиатора, но и в значительной мере от гидростатической части тензора напряжений, а нередко и от вида напряженного состояния. В общем случае формоизменение грунтов принято описывать функциональными нелинейными зависимостями, например, величин ε_i или Г от инвариантов Т, σ_ср и μ_σ как

ε_i = ε_i (σ_i, σ_ср, μ_σ) или Г = Г(Т, σ_ср, μ_σ). (8.4)

Зависимость формоизменения от σ_ср отличает нескальный грунт от конструкционных упругопластических материалов. Она обусловлена дисперсной (зернистой) природой грунта: чем большей величины среднее напряжение σ_ср действует в грунте, тем большие силы трения развиваются между частицами (зернами) грунта и тем труднее осуществляется под действием девиатора напряжений его формоизменение. Следует подчеркнуть, что деформация формы появляется исключительно при наличии девиатора, т.е. при σ_i > 0 или Т > 0. Из зависимостей (8.4) отнюдь не следует, что σ_ср также создает деформацию ε_i или Г, среднее давление лишь в большей или меньшей мере затрудняет формоизменение в зависимости от соотношения величин σ_i и σ_ср. Пример типичной зависимости ε_i от инвариантов σ_i, σ_ср, μ_σ для песка показан на рис. 8.1. Кривые, начиная с точки К, имеют горизонтальные участки, отвечающие разрушению образца при достижении предельного формоизменения. Аналогичный характер эти зависимости имеют и для глинистых грунтов, но в них влияние вида напряженного состояния и среднего давления выражено слабее, чем в несвязных грунтах.

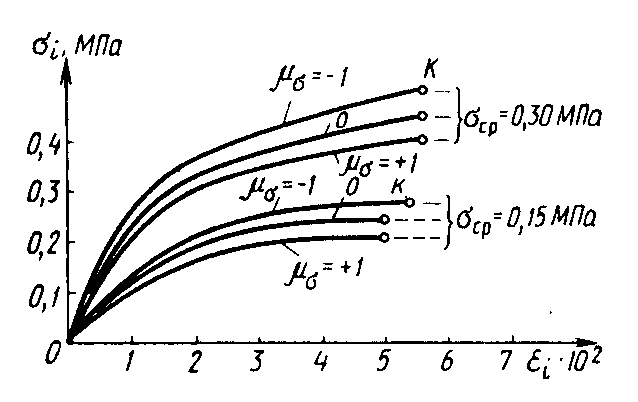
Рис.8.1. Зависимость формоизменения песка

от инвариантов напряженного состояния

Следует заметить, что для многих грунтов большая криволинейность графиков ε_i(σ_i) при σ_ср = const, μ_σ = const отмечается только при околопредельных состояниях, т.е. при подходе к горизонтальным участкам, а на большей части графиков (от нулевой точки) зависимость ε_i(σ_i) является линейной или близкой к ней. Как показывают эксперименты, для многих грунтов, особенно при медленных темпах нагружения, влиянием параметра μ_σ на формоизменение можно пренебречь, т.е. в расчетах вместо зависимостей (8.4) можно принимать ε_i = ε_i (σ_i, σ_ср) или Г = Г(Т, σ_ср). В практических расчетах экспериментальные кривые ε_i = ε_i (σ_i, σ_ср) иногда представляют степенными зависимостями вида

σ_i = A(σ_ср + b), (8.5)

но наиболее часто применяется их аппроксимация уравнением, предложенным А.И. Боткиным

, (8.5^/)

где А,В,b,m — параметры, подлежащие экспериментальному определению;

σ_iпр определяется выражением τ_окт.пр., в котором τ_окт.пр – прочность грунта по А.И. Боткину

τ_окт.пр = σ_окт · tgφ_окт + с_окт (8.6)

где σ_окт, τ_окт – нормальное и касательное напряжения на октаэдрической (равнонаклоненной к осям главных напряжений σ₁, σ₂, σ₃) площадке, определяемые зависимостями

σ_окт = (σ₁+ σ₂ + σ₃) = σ_ср,

τ_окт = _,

φ_окт , с_окт  — параметры прочности грунта (угол внутреннего трения и сцепление) в модели Боткина.

С учетом влияния μ_σ на формоизменение в правой части зависимостей (8.5) и (8.6) включается соответствующая функция f(μ_σ).

Объемная деформация грунта в большей своей части является пластической и зависит не только от среднего давления (шарового тензора напряжений), но и весьма существенно от девиатора напряжений и в некоторой степени – от вида напряженного состояния. Зависимость объемной деформации от девиатора напряжений (дилатансия грунта) принципиально отличает грунт от конструкционных материалов.

При анализе экспериментов среднюю ε_ср или объемную ε_V = 3ε_ср деформацию принято представлять суммой двух величин

ε_υ = +

или ε_ср = += ε_ср(σ_ср, σ_i, μ_σ), (8.7)

где — средняя деформация при гидростатическом обжатии давлением σ_ср при σ_i = 0, = (σ_ср). Второе слагаемое в (8.7) – это средняя дилатантная деформация, развивающаяся при данном σ_ср за счет воздействия девиатора и являющаяся функцией инвариантов σ_ср, σ_i и μ_σ, т.е. = (σ_ср, σ_i, μ_σ).

Зависимость деформации от всестороннего обжатия имеет вид типичной нелинейной кривой 1 (рис. 8.2), что также отличает грунт от таких материалов как металлы, у которых является упругой и линейно зависящей от σ_ср.

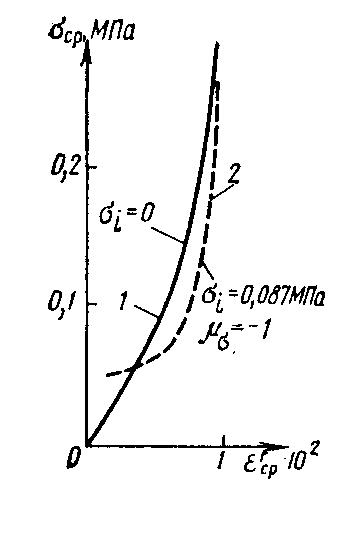
Рис. 8.2. Объемное деформирование песка при гидростатическом

(всестороннем) и девиаторном нагружении.

Весьма часто зависимость (σ_ср) для грунтов аппроксимируется дробно-линейной или экспоненциальной зависимостями:

σ_ср = ;

= [1 - exp (bσ_ср)],

где – предельное значение , достигаемое при σ_ср → ∞, когда грунт получает максимальную плотность; К₀, b - экспериментально определяемые параметры.

Зависимость дилaтантной деформации от инвариантов σ_i, σ_ср, μ_σ носит сложный характер. Вклад в суммарную деформацию ε_ср зависит от соотношения инвариантов σ_i и σ_ср. В частности, на рис. 8.2 кривая 2 характеризует зависимость ε_ср от σ_ср при постоянном σ_i.

В целом зависимости (8.4) и (8.7) отражают фундаментальные особенности деформирования грунтов – проявление внутреннего трения и дилатансии на всем пути деформирования, а также зависимость деформаций от вида напряженного состояния.

В экспериментах было установлено, что при простом нагружении^*) грунтов с достаточно высокой точностью соблюдаются подобие напряженного и деформированного состояний μ_ε = μ_σ и соосность главных направлений тензоров напряжений и деформаций.

В то же время для некоторых траекторий сложного нагружения нарушения соосности и подобия были весьма существенными. При этих нарушениях представление в расчетах грунта средой деформационной теории пластичности становится неправомерным.

Опыты с использованием различных сложных траекторий нагружения также показали, что при одном и том же конечном напряженном состоянии деформированное состояние грунтов зависит, и в ряде случаев существенно, от траектории нагружения или, как принято иногда говорить, от истории загружения. Степень влияния сложности нагружения на деформации ε_i и ε_ср различна в зависимости от вида грунта, начального его состояния, действующих напряжений и др. Например, только один поворот осей главных напряжений может давать изменение деформаций формы и объема на 30% и более от достигнутых на этот момент значений этих деформаций. Заметим, что ни модель линейной теории упругости, ни модель деформационной теории пластичности не допускают учета зависимости деформированного состояния от траектории нагружения.

Приведенные результаты, характеризующие нелинейное деформирование грунта, получены в экспериментах с образцами в предположении их изотропности. Это предположение основывается на том обстоятельстве, что испытаниям подвергались, как правило, искусственно приготовленные образцы-близнецы, чем практически исключалось или сводилось к минимуму создание в них анизотропии механических свойств.

По аналогии с изотропным грунтом, линейное или нелинейное деформирование которого характеризуется двумя постоянными или переменными модулями G и К, для трансверсально-изотропного нелинейно деформируемого грунта необходимо экспериментально установить изменение пяти характеристик в зависимости от напряженно-деформированного состояния [3], что делает соответствующие эксперименты с анизотропными грунтами чрезвычайно сложными и трудоемкими.