3. Определение напряжений и перемещений в грунтах.

В тех случаях, когда области предельного напряженного состояния грунта отсутствуют или невелики по сравнению с размерами сооружения, определение напряженно-деформированного состояния грунтового массива (основания, плотины, насыпи дороги и т.п.) выполняют, представляя грунт моделью линейно-деформируемой среды. Такой подход оправдан для многих расчетных случаев, в частности, при проектировании фундаментов многих сооружений. И по существу, как показано в разд. 3.1, сводится к использованию соответствующих решений линейной теории упругости (ЛТУ). Изложение методов получения решений ЛТУ входит в задачи курса теории упругости, поэтому ниже приводится лишь перечень некоторых имеющихся решений ЛТУ и для наиболее широко применяемых при расчете оснований конечные результаты решений.

Приводимые ниже аналитические решения задач ЛТУ получены^*) в напряжениях при представлении грунтовых оснований абстрактными схемами (моделями) полуплоскости или полупространства. Среда в этих схемах принимается однородной и изотропной и, как следствие, зависимость для напряжения σ_z не содержит деформационных характеристик Е, ν, т.е. σ_z не зависит от того, чем конкретно представлена среда (металл, бетон, грунт и др.). Напряжения σ_х , σ_у не зависит от Е, ν в плоских задачах, но могут зависеть от ν в пространственных задачах.

Напряжения от собственного веса грунта в основании с горизонтальной поверхностью.

При использовании модели ЛДС (ЛТУ) основание представляется «весомым» полупространством, ограниченным сверху плоской поверхностью.

В этом случае нет бокового расширения грунта и все компоненты напряжений в декартовой системе координат (z - вертикальная ось) определяются по зависимостям

, _x = _y = _z

_xy = _yz = _zx = 0 (3.23)

B однородном грунте (z) =  = const и _z = z, _x = _y = z, а в случае i слоев толщиной h_i и удельным весом  _i получаем _z,i = _i h_i, _x,i = _y,i = _i_zi.

На рис. 3.5. показана эпюра напряжений в слоистой среде, причем ниже горизонта грунтовых вод (ГГВ) учитывается взвешивание грунта водой.

Удельный вес взвешенного в воде грунта определяется, учитывая, что на твердые частицы кроме их веса (в воздухе) действует архимедова сила в объеме частиц, т.е.

_взв = _dg - m_вg = _d - m_{в =} _d –(1 – n) _в

Для многих грунтов _взв мало отличается от _в = 10 кН/м³.

Рис. 3.5. Напряжения σ_z от веса грунта в слоистой толще.

При изменении положения горизонта грунтовых вод сжимающие напряжения изменяются: при понижении ГГВ – увеличиваются (пунктир на рис. 3.4), при повышении ГГВ – уменьшаются, что соответственно приводит к осадкам или подъему поверхности основания.

Напряжения в грунте основания от собственного веса принято называть бытовыми или природными. В зависимостях (3.23) соотношение между _x, _y и _z определяется коэффициентом бокового давления . Из решения задачи ЛТУ этот коэффициент не определяется. В расчетах оснований величину  назначают обычно по результатам лабораторных определений (см. pазд. 2.1, 2.4). Иногда принимают  = 1, в этом случае природное напряженное состояние _x = _y = _z называют гидростатическим, а при значении ξ в условиях компрессионного нагружения – геостатическим. В действительности, величина  зависит от всей прошедшей истории образования и формирования толщи грунта, включая различные геологические процессы, и соотношение _x/_z в породах может быть, как показывают замеры, самым различным, в том числе _x/_z >1 ( > 1).

Перемещения основания, в том числе осадки его поверхности, от собственного веса грунта принимаются давно завершившимися и поэтому обычно не определяются. Однако, в том случае, если изменяется структура грунта, то вес грунта вызывает в нем дополнительные деформации и перемещения (осадки), например, при увлажнении просадочного грунта или оттаивании мерзлого грунта (см. разделы 2.1, 2.8). Эти деформации определяются инженерными способами с использованием результатов испытаний.

Напряжения и перемещения от внешних статических нагрузок.

Плоская задача.

В расчетной практике наиболее часто используется решение теории упругости для случая вертикальной равномерно распределенной полосовой нагрузки q, приложенной на участке 2а к поверхности основания (к краю полуплоскости) (рис. 3.6), полученное Г.В. Колосовым (1935 г) на основе решения Фламана для сосредоточенной силы [9,12]. В декартовой системе координат напряжения определяются по весьма громоздким формулам, которые для практического использования сводятся к простым зависимостям вида

s_z = k_z∙q, s_x = k_x∙q, τ_xz = k_xz∙q, (3.24)

где коэффициенты k_z, k_x, k_xz приводятся в таблицах для безразмерных координат x/2a, z/2a (см., например, [9, 12]). На рис. 3.6 а, б, в показаны линии равных напряжений s_z, s_x, τ_xz. По решению ЛТУ эти линии сходятся в краевых точках полосы загружения, что определяет большой градиент напряжений в грунте у краев полосы.

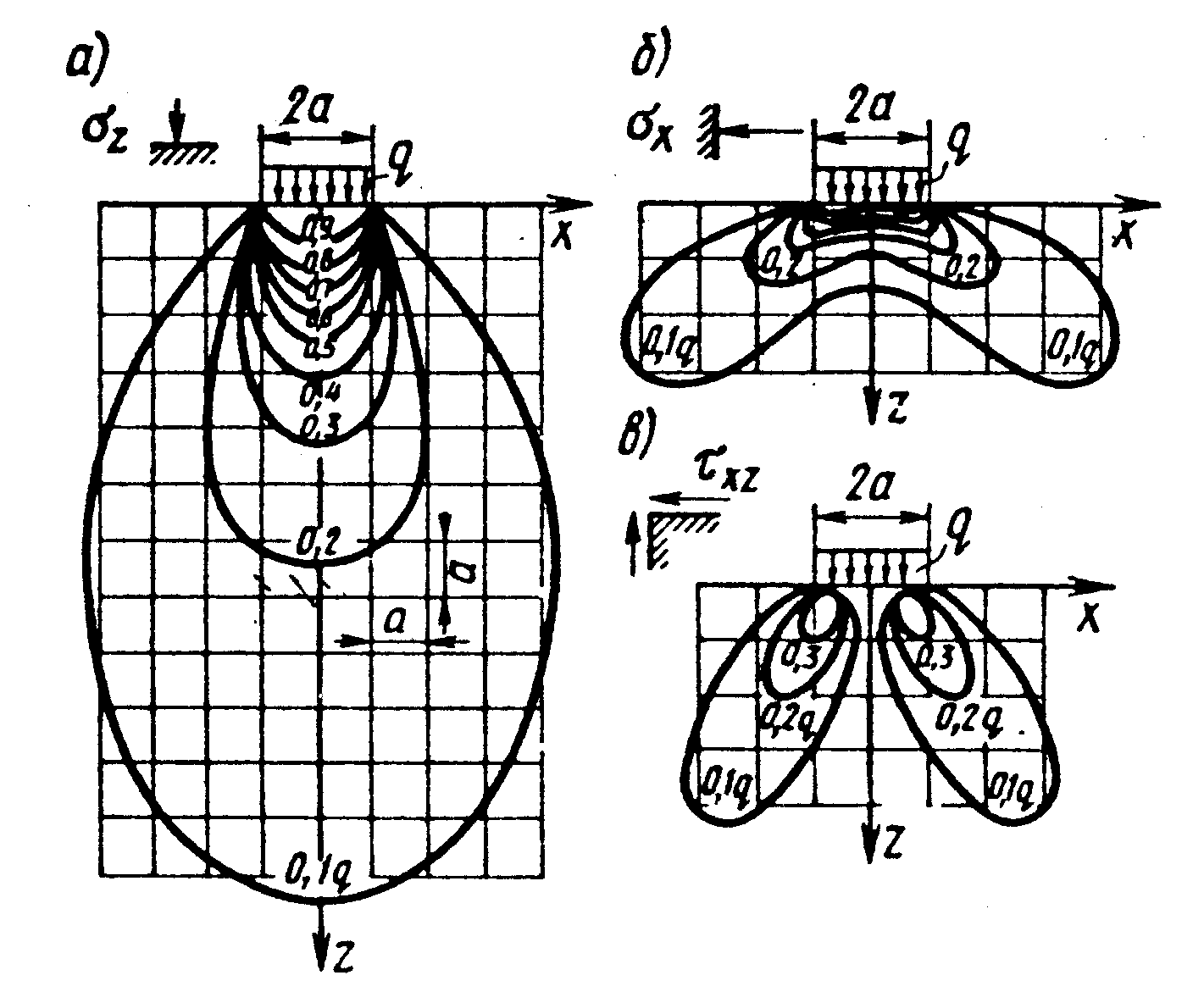
Рис. 3.6. Линии равных напряжений σ_z (a), σ_x (б), τ_xz (в) от вертикальной

распределенной по полосе нагрузки.

На рис. 3.7 приводятся эпюры напряжения s_z по различным горизонтальным и вертикальным сечениям. Согласно решению ЛТУ напряжения s_z распространяются по всему массиву основания, убывают с глубиной z и с расстоянием x и становится равными нулю в бесконечности (при z = ∞ или x = ∞).

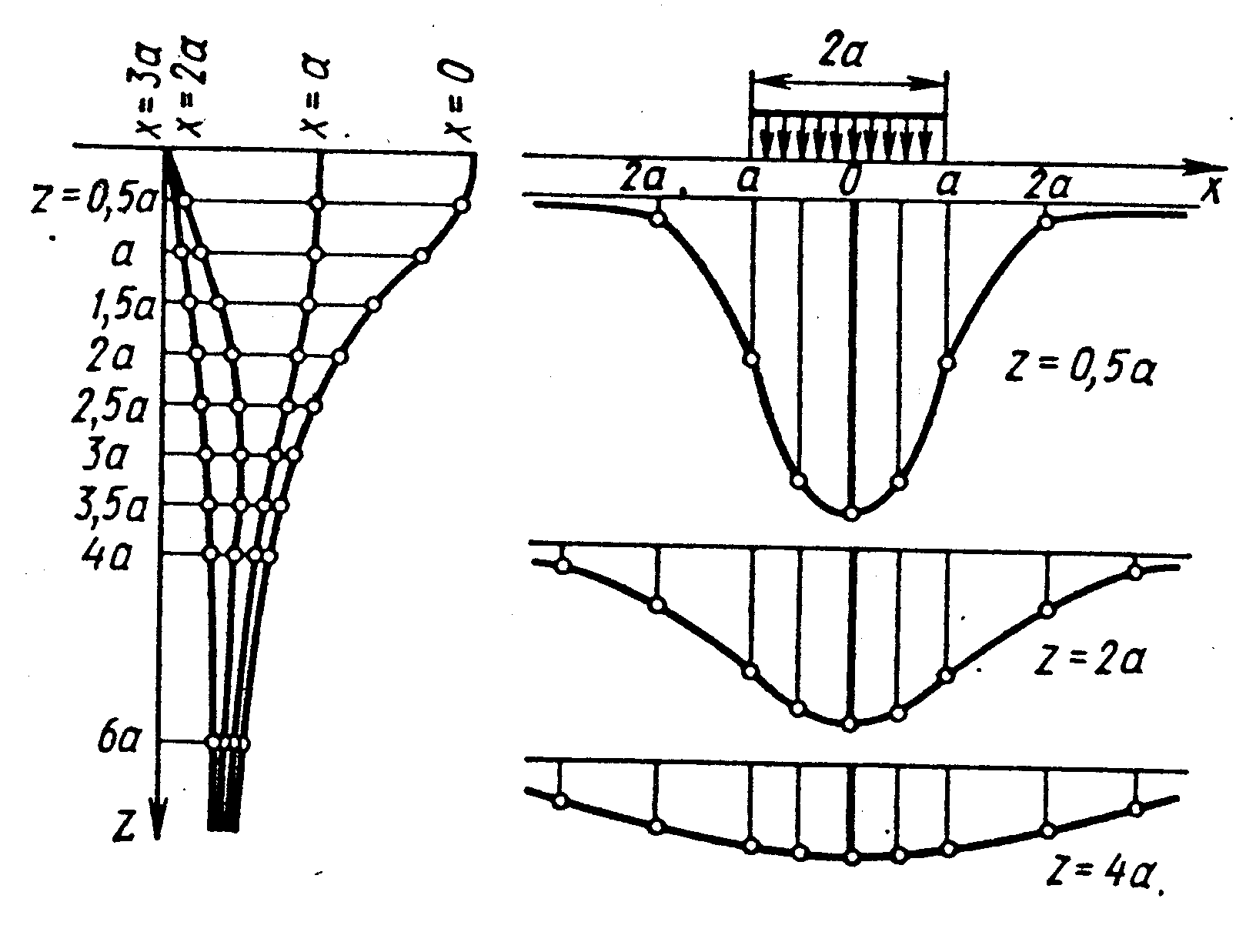
Рис. 3.7. Эпюры напряжения σ_z по вертикальным и горизонтальным сечениям основания от вертикальной полосовой нагрузки

Формула для осадки поверхности основания от полосовой нагрузки получена на основе решения Фламана для осадки от сосредоточенной силы [12]. По решению ЛТУ осадки полуплоскости определяются с точностью до произвольной постоянной, т.е. конкретная величина осадки по ЛТУ не определяется, можно лишь при необходимости найти разность осадок соседних точек поверхности основания.

Кроме варианта равномерной полосовой нагрузки имеются решения теории упругости и составлены таблицы напряжений для вертикальной нагрузки, изменяющейся на полосе 2а по закону треугольника, параболы, трапеции и др. [9, 12]. Используя принцип суперпозиции, может быть составлена любая необходимая комбинация из указанных нагрузок.

Так же как для вертикальных нагрузок, в ЛТУ получены решения для горизонтальных сосредоточенной силы и распределенных нагрузок. Наиболее полно результаты решений приводятся в [12].

Пространственная задача.

В расчетах иногда используется решение Буссинеска (1885 г.) для случая вертикальной сосредоточенной силы, приложенной к поверхности однородного упругого невесомого полупространства (рис. 3.8,а). В частности, вертикальное напряжение s_z определяется выражением

, (3.25)

где = и .

Выражение (3.25) для s_z можно записать в виде

, где 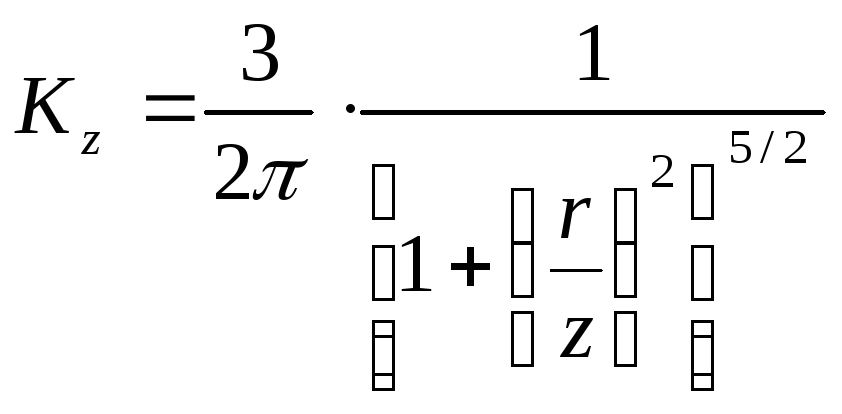. (3.26)

Cоставлена таблица значений К_z в зависимости от .

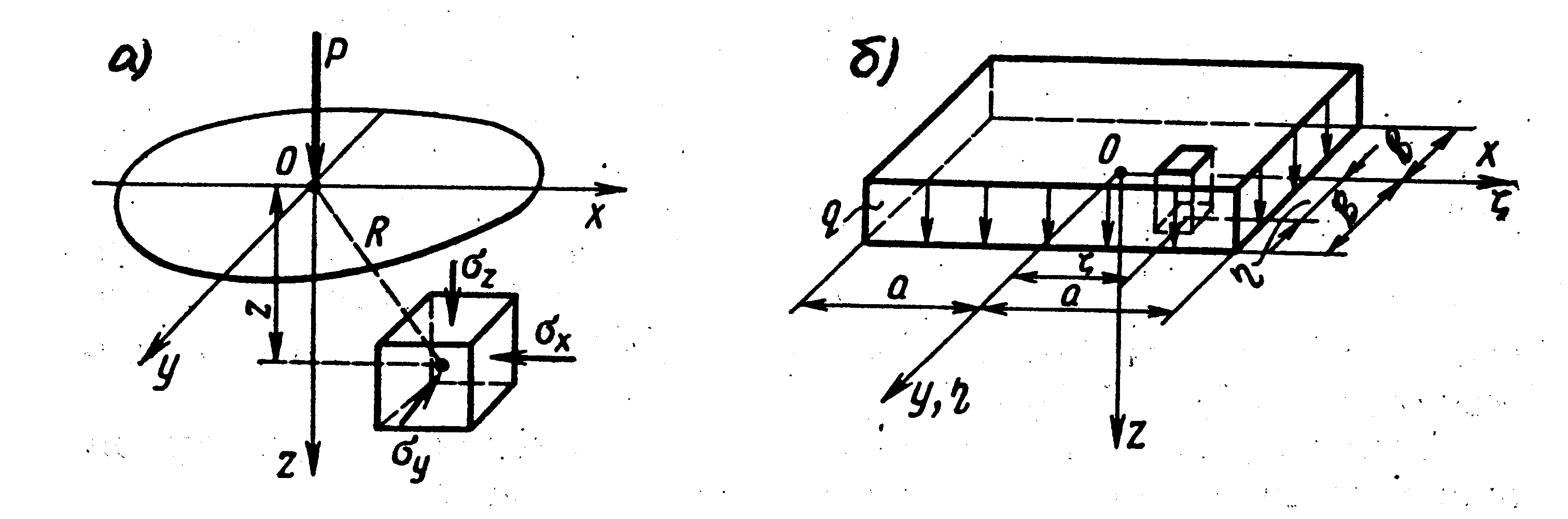
Рис. 3.8. Полупространство под действием приложенной к поверхности:

а – вертикальной сосредоточенной силы, б – вертикальной распределенной по площади прямоугольника нагрузки.

Весьма широкое применение находит решение (В.Г. Короткин, 1938 г.) для случая загрузки прямоугольной площади поверхности основания (полупространства) равномерно распределенной нагрузкой (рис. 3.8,б). Формулы для напряжений получены, используя решение Буссинеска [12]. Для определения напряжения s_z в точках угловой вертикали, т.е. вертикали, проходящей через один из углов прямоугольной площади 2а∙2b, составлена таблица коэффициента K_z в зависимости от n = b/а и m = z/2a [9,12]. Напряжение s_z определяется выражением s_z = K_z∙q. Эта же таблица позволяет найти s^ц_z на вертикали, проходящей через центр площади загружения (центральная вертикаль), используя известное соотношение: s^ц_z на центральной вертикали на глубине h равно учетверенному значению s_z на угловой вертикали на глубине 2h.

Вертикальные перемещения (осадки) точек центральной и угловой вертикалей получены в виде

W = 2q·а·К(z) , (3.27)

где К(z) – коэффициент, зависящий от безразмерных величин n=b/а и m=z/а, для указанных вертикалей приводится в виде таблиц в [9,12], в частности, для осадки поверхности (z=0) в центре квадратной (n=1) площади загружения К(z)=1.12, а для угловой точки – 0.56.

Следует подчеркнуть, что зависимость (3.27) характеризует осадки однородного (Е=const) полупространства, неограниченно простирающе-гося по осям x, y, z. В реальных основаниях имеет место значительное возрастание модуля деформации Е с глубиной из-за обжатия пород весом вышележащей толщи грунтов, что необходимо учитывать при определении осадок (методы такого учета изложены в гл.5).

На использовании таблицы (или формулы) для напряжения s_z в точках угловой вертикали основан способ угловых точек. Подчеркнем, что при применении этого способа должно всегда выполняться условие: площадь загружения должна так разбиваться на отдельные прямоуголь-ники, чтобы вертикаль, на которой определяется напряжение s_z, обязательно проходила через угол каждого отдельного прямоугольника. При необходимости вводят фиктивно загруженные прямоугольники, которые затем учитываются со знаком минус.

Если необходимо определить напряжение в точке на вертикали, не проходящей через одну из угловых точек участка загружения, то, как показано на рис. 3.9,а, необходимо разделить прямоугольную площадь загружения abcd на четыре прямоугольника: okam, ombe, okdn и oecn. Затем определить напряжения в точке 0(x, y, z) от загрузки каждого прямоугольника в отдельности по таблице и полученный результат сложить, т.е.

s_z (0) = s_z (okam) + s_z (ombe) + s_z (okdn) + s_z (oecn).

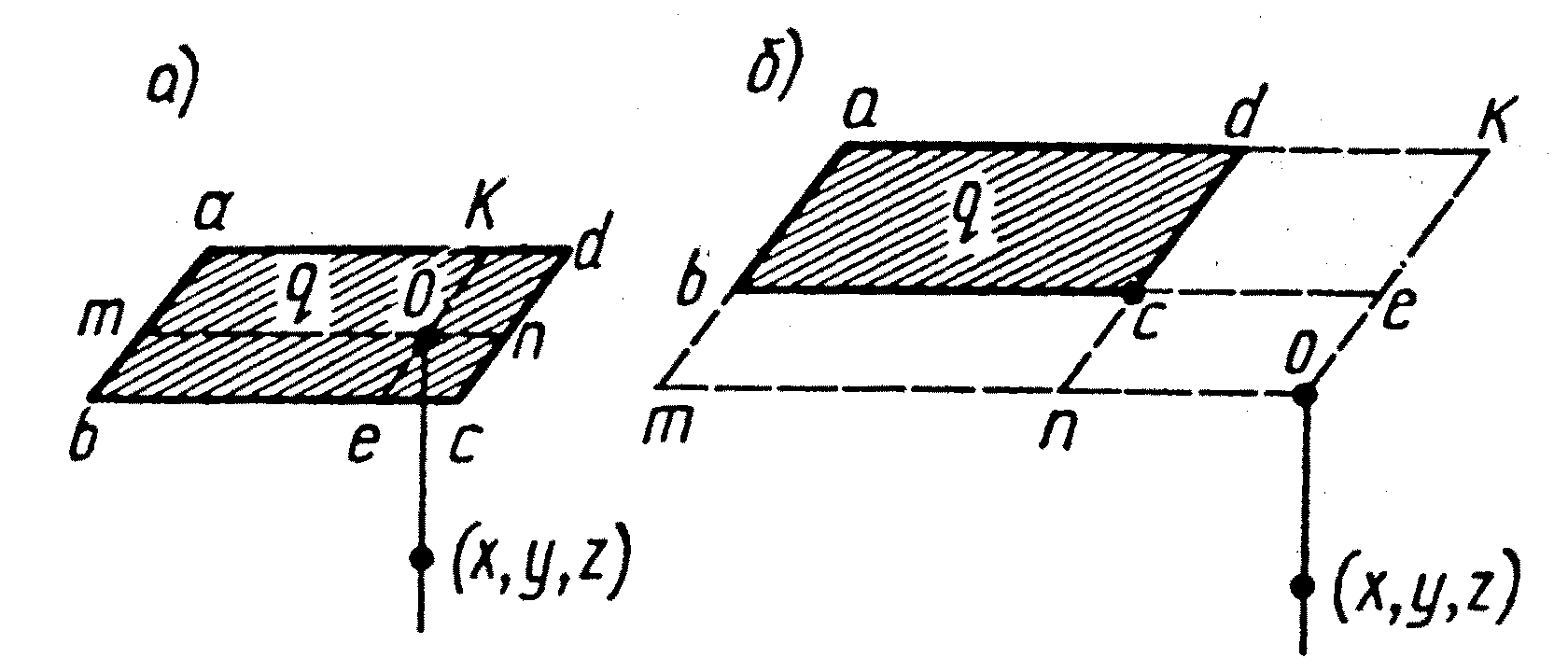
Рис. 3.9. Определение напряжений в основании способом угловых точек.

Eсли вертикаль, на которой находится точка, не пересекает площади загружения abcd, то в соответствии с рис. 3.9,б напряжения в этой точке определяются как алгебраическая сумма напряжений от загрузки прямоугольников:

s_z (0) = s_z (okam) - s_z (oebm) - s_z (okdn) + s_z (oecn).

Нетрудно показать, что способ угловых точек может быть с успехом применен и в тех случаях, когда нагрузки от сооружений различны и имеют в плане сложную форму.

При сложном очертании площади загружения (невозможна разбивка на прямоугольники) и сложном характере распределения нагрузки напряжения, например s_z, в какой-либо точке основания определяют способом сложения напряжения от элементарных нагрузок. Распределенную на площади А нагрузку заменяют набором сосредото-ченных сил (элементарных нагрузок) P_i = q_i∆A_i, где ∆A_i – элементарная (достаточно малая) площадка любой в плане формы, в пределах которой можно принять q_i = const; ∑∆A_i = A. Используя формулу (3.25) или (3.26) от каждой P_i находят s_z,i и их суммированием получают искомое s_z.

Помимо приведенных, в теории упругости имеются решения для ряда других схем загружения оснований, которые могут быть использованы в расчетах оснований.

В заключение подчеркнем, что в настоящее время для определения напряжений широко используются решения задач ЛТУ численными методами (МКЭ, МКР) на компьютерах, что делает расчеты оснований общедоступными при любом характере нагрузки и любом очертании площади загружения. В большинстве проектных организаций в компьютеры также введены ранее составленные таблицы (К_z, К_x, K_xz и т.д.) для автоматизированного определения напряжений от внешних нагрузок.

Напряжения от фильтрационных сил.

Движение воды в порах грунта (фильтрация) возникает в результате наличия различной величины напоров в различных точках основания, т.е. при .

При движении свободной воды между нею и скелетом (твердые частицы + связанная вода) возникают силы взаимодействия (рис. 3.10,а) в виде сил трения и сил давления по поверхности связанной воды. Равнодействующая R этих сил (рис. 3.10,б), приложенных ко всем твердым частицам, находящимся в единичном объеме, называется интенсивностью силы гидравлического воздействия потока. В расчетах обычно используют составляющие R, представленные вертикальной силой взвешивания (архимедовой силой), равной A = γ_в ∙ m, и силой Ф, называемой фильтрационной силой. В частном случае отсутствия фильтрации Ф=0, но всегда действует сила А.

Рис. 3.10. Схема сил, действующих на частицу грунта (а); архимедова и фильтрационная силы (б) потока на единичный объем грунта.

Дополнительное к силе взвешивания воздействие фильтрационного потока (u = k_ф∙I > 0) на скелет грунта выражается в виде объемных (т.е. действующих на каждый единичный объем грунта) фильтрационных сил Ф, направленных по линии тока. В свою очередь скелет грунта действует на воду тормозящей силой Т, равной по величине Ф, но обратной по направлению, т.е.

Т = - Ф. (3.28)

Фильтрационные силы вызовут развитие в грунте фильтрационных напряжений. Для их определения предварительно необходимо найти силы Ф, действующие в грунтовом основании в пределах фильтрационного потока.

Для определения интенсивности, т.е. удельной (действующей на единичный объем грунта) фильтрационной силы вырежем по линии тока s элементарную трубку грунта (скелет грунта и заполняющая поры вода) длиной ds и поперечным сечением А. Рассмотрим все силы, действующие только на поровую воду в трубке.

По торцам трубки (рис. 3.11) действуют силы давления воды: на одном торце – рА , на другом - . Давление воды действует также на боковую поверхность трубки. На рис. 3.11 оно не показано, поскольку это давление в уравнение проекции на ось s не входит. Внутри трубки действуют вес воды в порах, равный γ_вnAds, и сила, обратная архимедовой и равная γ_вmAds. Учет ее обязателен, так как, если вода взвешивает частицы с архимедовой силой, направленной вверх, то по принципу равенства сил действия и противодействия на воду будет действовать равная, но направленная вниз сила, обратная архимедовой. Кроме того, внутри трубки на движущуюся воду действует объемная тормозящая сила, равная TAds, которая направлена по оси s. Здесь Т - удельная, т.е. действующая на единичный объем грунта, тормозящая сила.

Рис. 3.11. Силы, действующие на воду при фильтрации

в элементарной трубке грунта.

Составляя уравнение равновесия всех сил, действующих на воду внутри грунтовой трубки, в виде их проекции на направление оси s, в соответствии с рис. 3.11 получим

pА - A+TАds- mγ_вAds∙sinα- nγ_вAds∙sinα=0,

oткуда, учитывая, что m+n=1, а , получим

и, имея в виду (3.28), находим

Ф= - . (3.29)

Проектируя фильтрационную силу на оси x, z, получаем составляющие объемной фильтрационной силы

X = - , Z = - , (3.30)

для определения численных величин которых необходимо располагать распределением напоров H = H(x, z).

При определении напряжений от объемных фильтрационных сил по модели линейно-деформируемой среды (теории упругости) исходными являются уравнения (3.2 . . . 3.4), в которых X и Z принимаются по (3.30). При сложном распределении фильтрационных сил по массиву основания решение задачи теории упругости можно получить численным методом, например, МКЭ. В ряде случаев при расчете оснований удобен подход (В. А. Флорин), основанный на эквивалентной замене фильтрационных сил фиктивными внешними нагрузками, приложенными к поверхности основания (см. подробнее в [9,12]).

Величина и направление фильтрационных сил существенно влияют на напряженно-деформированном состоянии основания. В частности, со стороны верхнего бьефа (В.Б.) в пределах от поверхности грунта до подошвы сооружения (плотина, перемычка и т.п.) фильтрационные силы направлены преимущественно вниз; со стороны нижнего бьефа (Н.Б.) – вверх (рис. 3.12,а). В случае нисходящего потока с I = const (рис. 3.12,б) напряжения σ_z на глубине z определяются зависимостью

σ_z = (γ_взв + Φ)·z = (γ_взв+γ_вI)·z ,

т.е. фильтрационный поток увеличивает напряжение σ_z по сравнению с напряжением γ_взв·z при Ф=0. Увеличение сжимающих напряжений σ_z вызывает дополнительные деформации уплотнения грунта, распространяющиеся под сооружение, что приводит к наклону сооружения в сторону В.Б. навстречу давлению воды (рис.3.12,а).

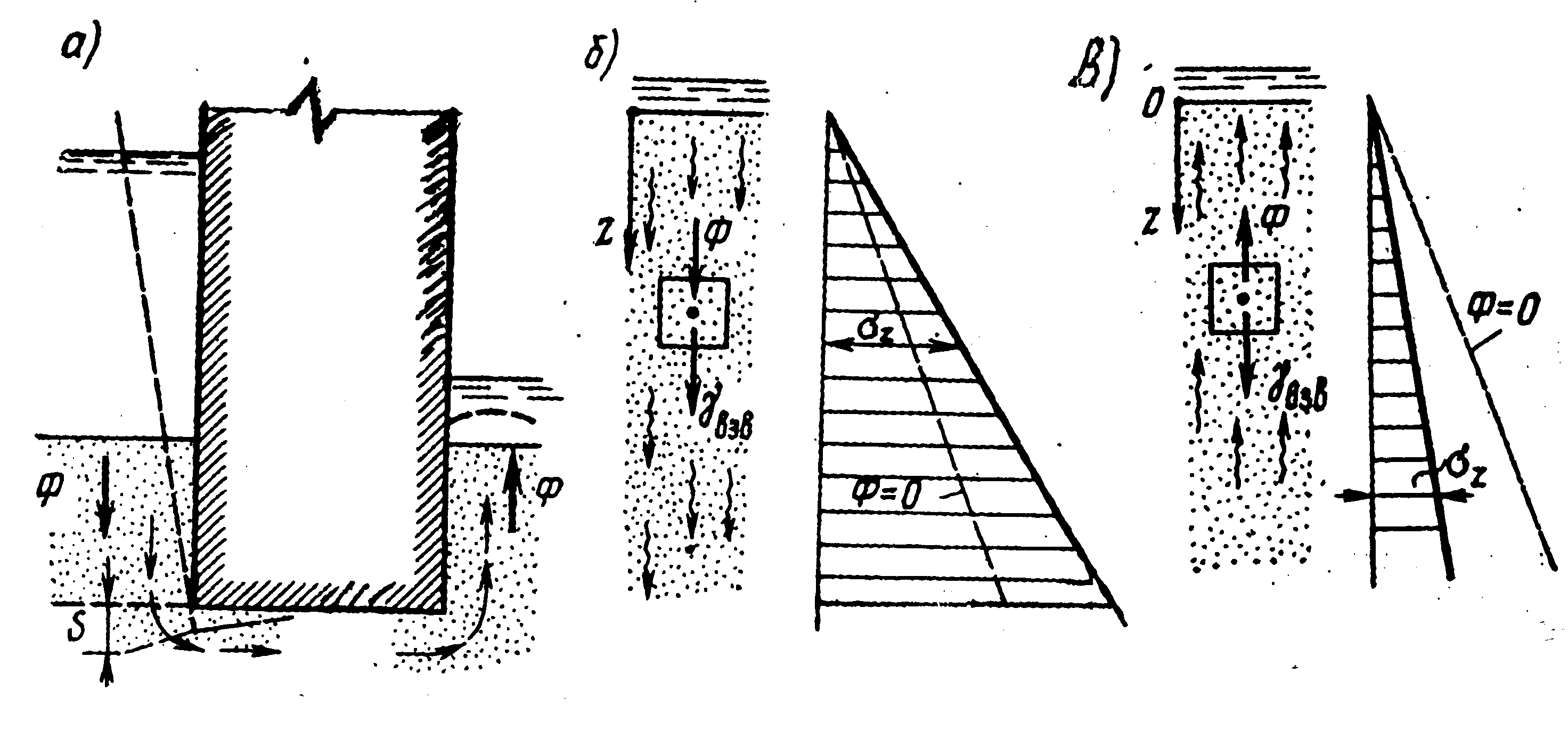
Рис. 3.12. Действие фильтрационных сил на основание сооружения

при разности уровней воды (а) и напряжения σ_z в грунте при нисходящем (б)

и восходящем фильтрационном потоке ( в).

При восходящем фильтрационном потоке с I=const силы γ_взв и Ф противоположны по направлению и σ_z = (γ_взв – γ_в· I)z (рис. 3.12,в) , т.е. происходит уменьшение сжимающих напряжений σ_z от фильтрационных сил. Аналогичное снижение σ_z имеет место при отрыве котлована с водоотливом, приводящим к формированию восходящего потока воды в котлован. В случае восходящего потока с удельными фильтрационными силами Ф = _в · I_кр = γ_взв на глубине z от дна котлована получаем σ_z = (γ_взв - -Ф)z = 0. Необходимый для этого градиент I_kp называют критическим градиентом напора. При критическом градиенте песчаный грунт (с = 0) не обладает сопротивлением сдвигу (при σ_z = 0 τ = σ_z ∙tgφ = 0). При малейшем превышении I значения I_kp песчаный грунт будет подниматься фильтрационным потоком (Ф > γ_взв), т.е. происходит так называемый фильтрационный выпор. В глинистом грунте выпор произойдет, если будет преодолено сопротивление грунта разрыву. Для исключения выпора применяют различные мероприятия (удлинение пути фильтрации, пригрузка грунта и т.п.) по уменьшению градиента напора I_в на выходе потока на поверхность до величины, которая существенно меньше I_kp (I_в ≈ 0,3). Заметим, что для большинства грунтов γ_взв ≈10 кН/м³ и I_kp≈1.