Для уравнения (7.10/) необходимо в (7.11) заменить е на nв/m.

Уравнения неразрывности компонент полностью водонасыщенного грунта.

Уравнение неразрывности для жидкой и твердой компонент грунта и для грунта в целом рассмотрим применительно к условиям плоской задачи. Поровую воду считаем несжимаемой, что оправдано для большинства практических задач консолидации грунтов.

Уравнение неразрывности жидкой компоненты грунта. Выделим, как показано на рис. 7.4, в грунте элементарный объем dx x dz x 1.

Тогда объем воды, вошедшей в элемент слева через грань dz за время dt будет u_xּdzּdt. Объем воды, вышедшей через правую грань dz определится как . Таким образом за счет горизонтальной составляющей потока воды в элементе добавится объем воды

u_xּdzּdt — =.

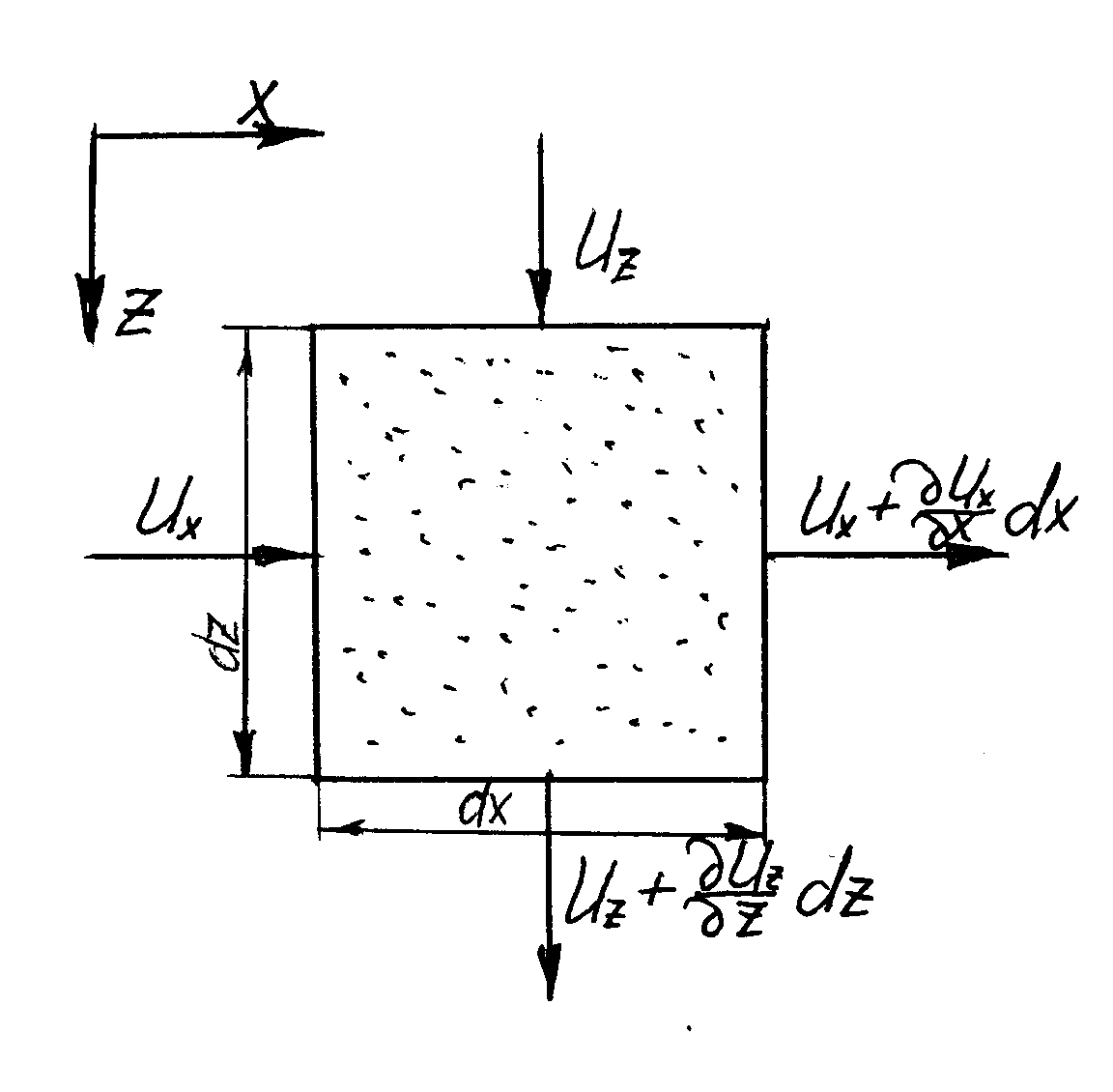
Рис. 7.4. Элемент грунта с входящими и выходящими потоками воды

для вывода уравнения неразрывности жидкой компоненты грунта

Аналогичным образом определится объем воды, который добавится в элементе за время dt за счет вертикальной составляющей потока. Этот объем составит . Суммарно в элемент добавится объем воды, равный

. (7.12)

В то же время объем воды, вошедшей в элемент, можно определить по изменению пористости (объема пор) грунта, остающегося полностью водонасыщенным.

Считаем, что в момент времени t грунт элемента имел пористость n, соответственно объем воды составлял n ∙dx ∙dz.

Через промежуток времени dt, т.е. в момент t + dt будем иметь: пористость и объем воды в элементе . Изменение объема воды в элементе, т.е. добавленный объем, составит

. (7.13)

Очевидно, что объемы воды, определяемые выражениями (7.12) и (7.13), являются одинаковыми, т.е. имеем

=

или

= 0. (7.14)

Уравнение (7.14) определяет неразрывность жидкой компоненты и означает, что суммарный объем воды, вошедшей в элемент (или вышедшей из элемента), равен изменению объема воды (объема пор) в элементе.

Уравнение неразрывности твердой компоненты грунта.

Заменяя в проделанных выше выкладках u на v и n на m и повторяя все рассуждения применительно к движению (фильтрации) несжимаемых твердых частиц, получим уравнение неразрывности (баланса объема) твердой компоненты в виде

= 0. (7.15)

Уравнение неразрывности в целом для грунта.

Складывая уравнения неразрывности (7.14) и (7.15) для жидкой и твердой составляющих грунта, и учитывая, что n + m = 1 и = 0, получим уравнение неразрывности водонасыщенного (двухкомпонентного) грунта в виде

= 0 или = - . (7.16)

Уравнение (7.16) означает, что в случае полностью водонасыщенного (двухкомпонентного) грунта объем несжимаемой воды, вошедшей в элемент (вышедшей из элемента), равен объему вышедших из элемента (вошедших в элемент) твердых несжимаемых частиц.

Уравнения неразрывности компонент трехкомпонентного грунта.

Уравнения неразрывности жидкой и твердой компонент применительно к условиям плоской задачи получаются аналогично уравнениям для водонасыщенного (двухкомпонентного) грунта.

Неразрывность жидкой компоненты определяется уравнением (7.14), в котором необходимо заменить n на n_в.

Неразрывность твердой компоненты определяется уравнением (7.15).

Уравнение неразрывности газообразной компоненты.

Газ в виде защемленных пузырьков при изменении давления и температуры может существенно изменять объем и, кроме того, растворяться в воде или выделяться из нее (см. раздел 1.1). Это следует учитывать при составлении уравнения неразрывности (баланса) газообразной составляющей грунта.

Масса газа, вошедшего внутрь элемента dx ∙dz (рис. 7.4) за время dt через обе грани dz, составит

= , (а)

а через грани dx соответственно

. (б)

Полагая, что поступающая в элементарный объем вода насыщена газом, принимаем, что температура грунта не меняется и масса растворенного газа определяется законом Генри (см. раздел 1.1). За время dt масса выделившегося газа может составить

μ_гּn_вּρ_гdxdz - . (в)

В то же время массу газа, вошедшего в элемент, можно найти по изменению содержания газа в элементе за время dt

dxdz = . (г)

Учитывая, что (а) + (б) + (в) = (г), уравнение неразрывности (баланса) защемленного газа получаем в виде:

= .

Обычно принимают μ_гּn_в = const. В этом случае, после дифференцирования, уравнение баланса принимает вид

w_xּ w_zּ+++ (s + μ_гּn_в) ּ= 0.

Уравнение неразрывности трехкомпонентного грунта в целом получается при сложении уравнений неразрывности жидкой, твердой и газообразной компонент, приведенных выше. В результате получаем:

++ + + + + w_xּ

+ w_zּ(s + μ_гּn_в) ּ= 0. (7.16^/)

В случае отсутствия газа (s = 0) уравнение (7.16^/) переходит в (7.16).

Для газообразной компоненты грунта в расчетах принимают в качестве уравнения состояния зависимость Бойля-Мариотта (см. раздел 1.1):

ρ_г = (р₁ + р),

где α – газовая постоянная; р₁ – начальное (до процесса консолидации) давление в воде, включая атмосферное; р – избыточное поровое давление. После дифференцирования уравнение состояния принимает вид

= .