7. Уплотнение водонасыщенных грунтов при длительно

действующих статических нагрузках (основы теории

консолидации).

1. Основные представления теории консолидации и этапы ее развития.

Консолидация — это уплотнение водонасыщенного грунта во времени путем сближения его твердых частиц, связанное с уменьшением объема пор и отжатием (удалением) части поровой воды из грунта. Начальные представления о процессе консолидации применительно к уплотнению (разуплотнению) грунта в компрессионном приборе были даны уже выше в разделе 2.1.

Как известно, характер сжатия грунта в компрессионном приборе (рис. 2.5) соответствует схеме одномерного (по вертикали) деформирования слоя грунта, бесконечно простирающегося в горизонтальном направлении и нагруженного по всей поверхности равномерно распределенной нагрузкой q (рис. 7.1). Выделенная в грунтовом слое призма находится в условиях, аналогичных условиям испытания грунта в компрессионном приборе. Из условия равновесия действующих на призму (площадь сечения А = 1) нагрузок q, σ_t, p_t (рис. 7.1) следует (см. формулу 2.6) соотношение

q = σ_t + p_t . (7.1)

Как и в разделе 2.1, соотношение (7.1) представляют в виде

σ_t = σ^*- p_t. (7.2)

В теории консолидации входящие в зависимость (7.2) величины принято называть: напряжения в скелете σ_t — эффективными, давления в воде p_t — нейтральными, а σ^* — тотальными (полными) напряжениями. При q = const имеем σ^* = q и σ^* является напряжением в стабилизированном состоянии (см. раздел 2.1).

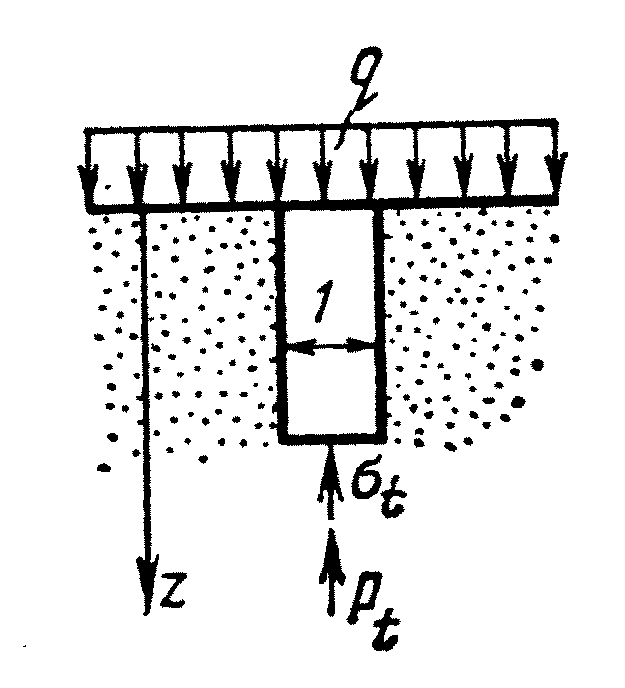
Рис. 7.1. Передача внешней нагрузки на скелет грунта

и поровую воду в случае одномерной задачи.

Процесс консолидации слоя водонасыщенного грунта (рис. 7.1) и образца грунта в компрессионном приборе (рис. 2.5) наглядно представляется с помощью простой механической модели, предложенной К. Терцаги (рис. 7.2). В этой модели элемент водонасыщенного грунта имитируется сосудом (цилиндром) с поршнем и пружиной, заполненным несжимаемой водой. Соответственно пружина моделирует скелет грунта, понятие которого дано в гл. 1, вода в сосуде представляет поровую воду, а определенного диаметра отверстие в поршне характеризует водопроницаемость грунта.

Рис. 7.2. Механическая модель К. Терцаги, иллюстрирующая

процесс консолидации элемента слоя водонасыщенного грунта.

В момент t = 0 приложения к поршню нагрузки q вода через отверстие еще не начала выходить и поршень осадку не получает, пружина остается недеформированной и поэтому усилие в ней отсутствует, т.е. в момент t = 0 в скелете σ_t=0 = 0. Из (7.1) следует, что вся нагрузка q передается на воду, т.е. дополнительное (сверх гидростатического) давление p_t=0 = q (рис. 7.2,а). Затем при t > 0 через отверстие в поршне начинается излив воды в виде фонтанчика (рис. 7.2,б). Объем воды в цилиндре уменьшается и поршень постепенно оседает, сжимая пружину, что соответствует появлению напряжений σ_t в скелете грунта, т.е. в любой момент t > 0 нагрузка q передается и на воду и на скелет. При этом выполняется условие равновесия (7.1). В момент, когда пружина получает сжатие, отвечающее всей нагрузке q, а поршень прекращает дальнейшее оседание, наступает стабилизированное состояние: усилие в пружине (напряжение в скелете) σ* = q, а дополнительное давление в поровой воде p = 0 (рис. 7.2,в). Таким образом, в течение всего периода консолидации напряжения в скелете изменяются от 0 до q, а дополнительное давление в поровой воде от q до 0. В соответствии с условием равновесия (7.1) приращение напряжения в скелете в любой момент времени равно падению давления в поровой воде.

Следует заметить, что изложенный процесс одновременного изменения σ_t и p_t справедлив только для схемы одномерной консолидации, для которой условие (7.1) выполняется строго. В случае плоской и тем более объемной (пространственной) схемы деформирования грунта уже в момент t = 0 приложенная нагрузка не передается полностью на воду, часть нагрузки воспринимается скелетом грунта.

Поскольку в процессе консолидации происходит изменение как напряжений в скелете, так и давлений в поровой воде, то соответственно происходят процессы деформирования скелета грунта и неустановившегося движения (фильтрации) воды, заполняющей поры грунта. Поэтому теория консолидации может рассматриваться как задача неустановившейся фильтрации в деформируемой грунтовой среде.

Постановка задачи теории консолидации в указанном аспекте во многом принадлежит отечественным ученым. Уравнение неустановившейся фильтрации при переменных значениях пористости и проницаемости грунта впервые было дано Н.Н. Павловским в 1922 г. Значительным этапом развития теории консолидации явились работы Н.М. Герсеванова, в частности, его капитальный труд «Динамика грунтовой массы» (1933 — 1937 г.г.), где приводится (однако, неполного состава) система уравнений пространственной задачи. За рубежом ряд одномерных задач консолидации был решен уже в 1925 г (К. Терцаги). Переход же к плоским и объемным задачам был осуществлен много позднее (в 1940 — 1950-х годах).

Важнейшим этапом развития теории консолидации явились работы В.А. Флорина, опубликованные в 1938, 1939 гг. В них была дана полная постановка плоской и пространственной задач консолидации треxкомпонентного грунта в рамках так называемой модели объемных сил. За рубежом аналогичная постановка была дана позднее, в 1941 г, М.А. Био.

В 1947. . .1948 г.г. В.А. Флорин предложил решение задач консолидации в предположении модели грунта, названной им «основной расчетной», позволяющей учитывать самые разнообразные свойства и особенности деформирования грунта. Заметим, что именно этот вариант теории консолидации использовался многие десятилетия для решения практических задач и до сих пор остается широко применяемым. В рамках этой модели В.А. Флориным в 1950 . . .1960 г.г. был предложен учет при консолидации наличия защемленного газа, ползучести скелета грунта, начального градиента напора, переменности характеристик грунта, постепенности возведения и конструктивных особенностей сооружения и др. [12].

Учитывая, что расчеты консолидации (уплотнения) водонасыщенных оснований фундаментов сооружений в настоящее время осуществляется, как правило, в рамках основной расчетной модели Флорина, в данной главе изложение теории консолидации в первую очередь приводится применительно к этой модели.

При выводе уравнения, описывающего процесс консолидации, приходится использовать ряд вспомогательных зависимостей, физических предпосылок и допущений, приводимых ниже.