4. Определение напряжений по подошве сооружений

Внешние силы, приложенные к сооружению, и его собственный вес передаются подошвой сооружения (точнее, подошвой его фундамента) на основание в виде нормальных и касательных напряжений (на рис. 4.1,а,б показаны только нормальные напряжения).

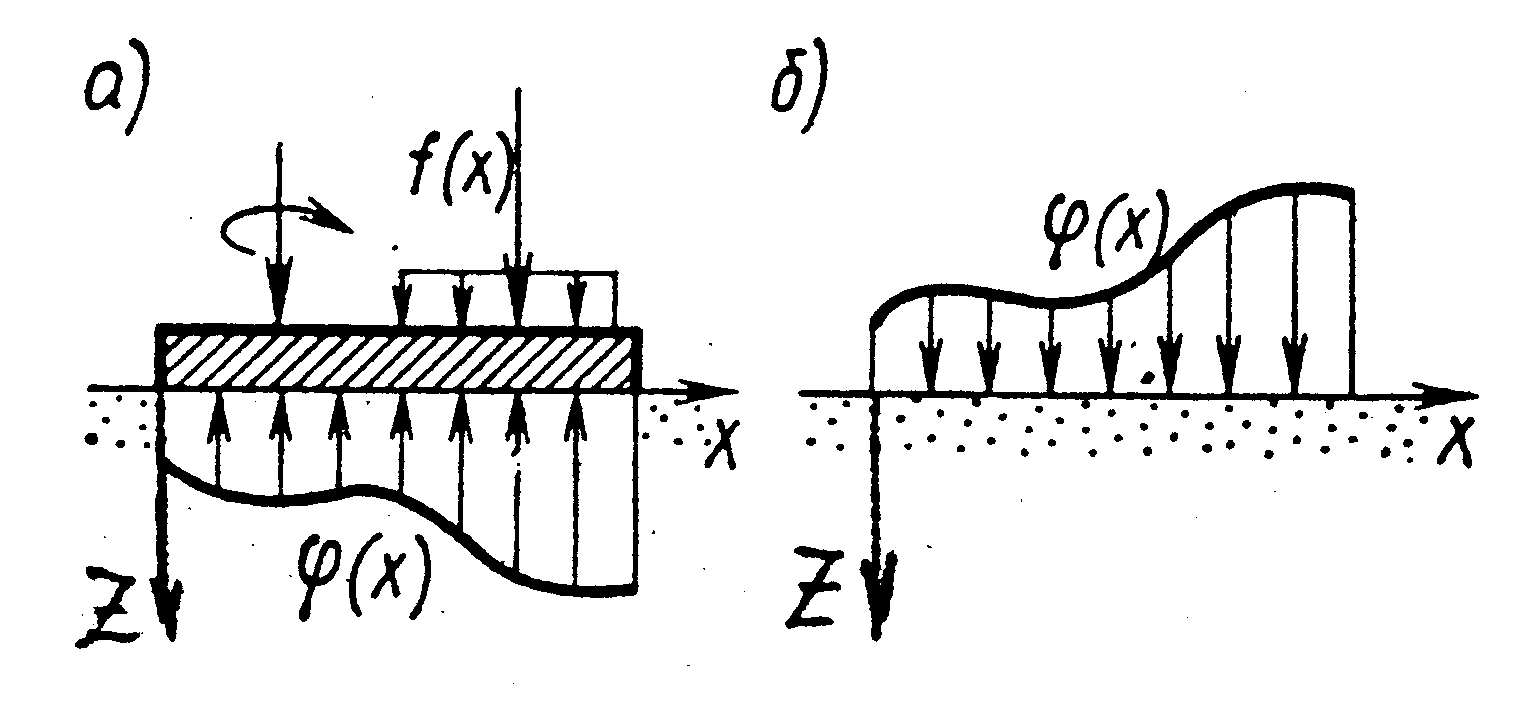
Рис. 4.1. Схема внешней нагрузки на сооружение и реактивные

нормальные напряжения φ(x) по подошве (а);

нагрузка φ(x), передающаяся сооружением на основание (б).

Эти напряжения для основания являются внешней нагрузкой (рис. 4.1,б) и их определение позволяет перейти к расчету напряженного состояния основания методами, рассмотренными в главе 3, и затем к расчету деформаций основания и перемещений сооружения (см. гл.5). Одновременно по подошве сооружения (рис. 4.1,а) со стороны основания (в силу 3-го закона механики Ньютона) действуют реактивные усилия, равные по величине нагрузке на основание, но противоположные по направлению. Их необходимо учитывать при определении величин внутренних усилий (М, Q, N и др.), по которым оценивается степень и характер армирования фундаментных железобетонных конструкций.

1. Расчетные схемы сооружений и модели оснований.

В зависимости от соотношения деформируемости основания и сооружения (или его фундамента) при определении напряжений по подошве возможны три расчетных случая:

1. Деформируемость сооружения (фундамента) столь велика, что его можно считать абсолютно гибким, точно следующим за деформациями основания, не влияя на них. Характерный пример – резервуары под жидкие или сыпучие материалы, тонкое металлическое или железобетонное днище («фундамент» резервуара) которых практически без изменения передает на основание нагрузку, действующую на верхнюю плоскость днища. Таким образом, для отмеченной категории сооружений определение напряжений по подошве заменяется определением нагрузок, приведенных к сечению сооружения на уровне его подошвы.

2. Деформируемость сооружения настолько мала по сравнению с деформируемостью основания, что сооружение можно считать недеформируемым или, как принято обозначать, абсолютно жестким.

3. B случае соизмеримости деформаций основания и сооружения последнее рассматривается как сооружение конечной жесткости.

Учитывая, что для большинства сооружений, зданий основные нагрузки имеют вертикальное направление (вес конструкций, оборудования и т.п.), в первую очередь разрабатывались методы определения нормальных напряжений (давлений) по подошве (φ(x) на рис. 4.1,а). Эти методы и рассматриваются подробно ниже.

Методы определения реактивных (нормальных) давлений основания на подошву сооружений как абсолютно жестких, так и конечной жесткости долгие годы развивались с использованием двух моделей основания: модели, в которой характеристикой основания является коэффициент постели, и модели линейно-деформируемого основания (ЛДО). Начиная с 1970-80-х годов, идет активное внедрение в практику расчета оснований, включая определение реактивного давления по подошве сооружений, упругопластических моделей грунта.

Модель коэффициента постели была предложена еще в 1801 г. русским академиком И.И. Фуссом, позднее, в 1867 г. ее независимо предложил и реализовал в расчетах Е. Винклер. С учетом истории появления эту модель следует называть моделью Фусса – Винклера, но, поскольку все практические применения ее начались в конце XIX века с Винклера, она во многих работах называется «моделью Винклера или «основанием Винклера».

В этой модели принимаются два существенных допущения: первое – осадка W(х,у) точки поверхности основания прямо пропорциональна величине нагрузки р(х,у) в этой точке (такая пропорциональная зависимость выполняется и в модели ЛДО), второе – осадки происходят только в месте приложения нагрузки, а за пределами площади загружения W(х,у) = 0.

Согласно этим допущениям осадки W поверхности основания Винклера под нагрузкой р формируют осадочную воронку, зеркально повторяющую характер изменения нагрузки (рис. 4.2.,а). В случае сосредоточенной силы осадка происходит в месте ее приложения, а в соседних точках W = 0 (рис. 4.2.,б). В целом основание Винклера образно иллюстрируется механической моделью в виде отдельных, не связанных между собой, пружин (рис. 4.2,в).

Рис. 4.2. Осадка основания Винклера от распределенной нагрузки р (а)

и от силы Р (б); механическая модель основания Винклера (в).

В модели коэффициента постели в соответствии с первым допущением принимается, что

p = k∙W. (4.1)

В случае задачи плоской деформации (рис. 4.1,б) погонная нагрузка φ(x) выражается через p(x,y) как φ(x) = p∙b и зависимость (4.1) принимает вид

φ(x) = b∙k∙W(x), (4.2)

где b – размер площади загружения в направлении, перпендикулярном плоскости деформации (в направлении оси «у»), при этом нагрузка и осадка вдоль оси «у» не меняются, т.е. р(x,y) = р(x), W(x,y) = W(x).

Коэффициент пропорциональности k носит название коэффициента постели. Из зависимости (4.1) при W(x) = 1 получаем p = k, т.е. коэффициент постели k численно равен давлению р, которое следует приложить к поверхности основания, чтобы получить осадку, равную единице. Соответственно коэффициент постели имеет размерность МПа/см, МПа/м (кгс/см³, тс/м³).

Подчеркнем, что модель коэффициента постели по ее физической сущности применима только для определения напряжений по подошве сооружения и осадок поверхности основания в пределах контакта его с сооружением без определения напряжений и деформаций в основании, т.е. это специфическая модель, пригодная только для решения контактной задачи.

Рис. 4.3. Сосредоточенная сила (а) и распределенная нагрузка (б),

приложенные к линeйно-деформируемому основанию.

Модель линейно-деформируемого основания базируется на представлении грунта моделью линейно-деформируемой среды (см. раздел 3.1) и в противоположность модели коэффициента постели постулирует осадки поверхности основания и за пределами площади загружения. Согласно этой модели от приложенной силы Р_ζ (рис. 4.3,а) любая точка поверхности линейно-деформируемого основания с координатой x получает осадку W(x), которая прямо пропорциональна величине силы Р_ζ и зависит от расстояния (x — ) между точкой приложения нагрузки и точкой с координатой x, т.е. осадку можно представить в виде

, (4.3)

где F(x — ) – функция от расстояния (x — ), принимающаяся по соответствующему решению линейной теории упругости (см. ниже).

Для случая распределенной нагрузки φ() (рис. 4.3,б) имеем dP_ζ = φ()d, из (4.3) dW = φ() F(x - ) d и осадка W(x) от φ() определяется интегрированием

. (4.4)

B отличие от модели Винклера модель линейно-деформируемого основания позволяет после определения φ() найти напряженно-деформированное состояние грунта во всей области основания от нагрузки φ(x) = - φ().

Переходим к определению напряжений по подошве сооружений с использованием приведенных, а также других моделей с последующим выявлением области их применения.