Лекция 2

Глава 2. Вычисление основных демографических показателей

2.1. Оценки средней численности населения и ее изменений.

Средняя численность населения S определенного населенного пункта для периода времени от t₁ до t₂ вычисляется по формуле:

(2.1.)

где — численность населения на начало рассматриваемого года.

— численность населения на начало следующего года.

Например, если известно, что принятая за численность жителей Ленинградской области на январь 1990 г. составила 1 656 тыс. чел., а в момент t₂, — на январь 1995 г. равнялась 1 667 тыс.чел., то среднее значение этого показателя для пятилетия равнялось (1 656 + 1 667) / 2 = 1661, 5 тыс.чел.

Это средняя численность жителей одного и того же региона для интересующего нас пятилетия. Но в демографии вычисляют среднее значение численности населения двух или более населенных пунктов.

Например, «формально» можно получить оценку , средней численности питерцев и жителей Ленинградской обл., скажем, на январь 1995 г. Но этот показатель для демографии не представляет интереса. А вот средняя численность жителей сельского населенного пункта, допустим, деревни Ленинградской обл., несомненно интересует демографов. Формула для ее вычисления такова:

(2.2)

где i — порядковый номер населенного пункта, S_i — число жителей в населенном пункте. В Ленинградской области в 2 952 деревнях проживает 34% от общей численности — 564 тыс. чел.. Таким образом, согласно формуле (2.2.) на каждую деревню приходится в среднем 19 жителей. Это означает, что большинство деревень насчитывают от 1 до 10 дворов, семейств. Кривая распределения численности выглядит далекой от гаусовского, нормального распределения. Резко скошена влево. Вершина максимальной частоты (доли, процента) — так называемая мода кривой распределения далеко стоит от средней выборочной, медианы.

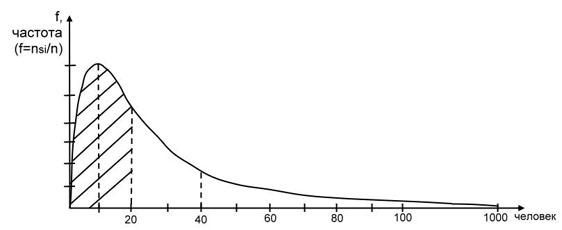
Рис. 2.1. Приблизительный вид кривой распределения числа жителей деревень Ленинградской и других областей Северо-Запада РФ.

В какой мере пригоден этот показатель для экономистов управленцев?

Оставим без внимания пока математико-статистическое значение этого распределения. Для оценивания проблем менеджмента, трудностей социальной жизни, культурно-просветительного обеспечения важно учесть, что в 25% деревень может не быть ни одного ребенка, 50% — 2-3-, а в 75% деревень насчитывается всего по несколько человек детей. Приходится закрывать школы, лечебные учреждения и пр.

2.2. Показатели рождаемости и смертности.

Общий коэффициент рождаемости вычисляется как частное от деления числа новорожденных N_i за интересующий нас i-тый год к средней численности в том же году

Получаем показатель физически безразмерный. Чаще всего он употребляется в тысячных долях или промиллях:

промилле (2.3)

Общий коэффициент смертности вычисляется аналогично, как отношение числа умерших M_i в течение i-ого года к средней численности населения в том же году

Он также безразмерный; чаще всего выражается в тех же относительных величинах, обозначенных промиллями:

промилле (2.4)

Третий фундаментальной важности демографический параметр — это показатель естественного прироста (или убыли) населения k, который вычисляется как разность между общим коэффициентом рождаемости и коэффициентом смертности m:

, промилле (2.5)

Формулы для получения трех фундаментальной значимости демографических оценок — m, n и k — чрезвычайно просты. Но для их запоминания и уяснения значения этих важнейших параметров, давайте сообща потренируемся в решении простейших демографических задач, а также в использовании результатов вычислений для анализа демографической ситуации. Правда, «сообща» мы сможем решать, если в нашем распоряжении имеются простейшие калькуляторы.

На основании опубликованных материалов по статистике населения [4; 27], вашему вниманию предлагаются данные таблицы 2.2.

Таблица 2.1.

Данные статистики населения Петербурга, Ленинградской области и Российской Федерации.

Год		1987	19901	1994
Население Петербурга	Родилось (чел), N Умерло (чел), М Средняя числен.насл. (тыс.чел.)	73 275 58 270 0,5 (4882,2+ +4931,2)= =4906,7	54 322 61 534 0,5 (4986,9+ +5023,5)= = 5005,2	34 563 83 647 0,5 (4952,3 + +4882,6)= =4917,4
Население Ленинградской области	Родилось (чел), N Умерло (чел), M Средняя числен. населен.(тыс.чел.)	23 631 18 625 0,5(1628,2+ +1612,4) = =1620,3	18 310 20 873 0,5(1653,6+ +1656,6)= =1655,1	12 339 32 453 0,5(1666,7+ +1661,4)= =1664,0
Население России	Родилось (чел.) N Умерло (чел.) М Средняя числен. насел.(тыс.чел.)	2 456 000 1 571 000 142 800	1 794 600 1 690700 148 320	1 395 000 2 211 000 148 400

На основании приведенных данных, по формулам (2.3) — (2.5), мы получили приведенные в табл. 2.2. значения интересующих нас показателей, оценивающих демографический статус населения трех регионов в три временных периода — 1987, 1990 и 1994 гг.

Таблица 2.2.

Значения общих коэффициентов рождаемости n , смертности m и показателей естественного прироста (убыли) населения k (значения показателей в

промилях)

Год		1987	1990	1994
Население Петербурга	Рождаемость, n Смертность, m Прирост, k	14,9 11,9 3,0	10,8 12,3 -1,5	7,0 17,0 -10,0
Население Ленинградской области	Рождаемость, n Смертность, m Прирост, k	14,6 11.% 3.1	11,1 12,6 -1.5	7,4 19,5 -12,1
Население РФ	Рождаемость, n Смертность, m Прирост, k	17,2 11,0 0,2	12,1 11.4 0,7	9,4 14,9 -5,5

Во всех трех регионах в рассматриваемое семилетие демографическая ситуация должна быть оценена как начавшийся процесс депопуляции, вымирания населения. Это наглядно подтверждает графический ход кривых динамики показателей, изображенных на рис 2.2. В частности, легко убедиться в том, что демографическая ситуация в городе на Неве и Ленинградской области демонстрирует более глубокое проявление процесса вымирания населения.

Рис. 2.2. График динамики показателей n, m и k, рассчитанных для населения трех регионов — Петербург, Ленинградская область, Российская Федерация (по данным табл. 2.2).

Суммарный коэффициент рождаемости — средне число детей, рожденных женщиной возраста 15-49 лет за всю ее жизнь:

(2.3)

где — средняя численность женщин возраста 15-49 лет (живущих в данный период); N — численность детей, рожденных этими женщинами.

Специальный коэффициент рождаемости F — отношение численности новорожденных за i-тый год к среднегодовой численности репродуктивного возраста, живущих в этом же году

(2.4)

Если известна доля женщин d_r репродуктивного периода в составе общей среднегодовой численности населения, , тогда значение специального коэффициента рождаемости F может быть получен путем деления n — общего коэффициента рождаемости на d_r:

Значения специального коэффициента рождаемости F, по понятным причинам в 3 -4 раза больше значения n; тот и другой показатель выражается обычно в промиллях.

Краткое содержание лекции и вопросы по её тематике.

Тема лекции — вычисление основных демографических показателей. В ней было дано определение и приведена формула для вычисления следующих показателей: средняя (в том числе среднегодовая) численность населения , значение общего коэффициента рождаемости n, общего коэффициента смертности m и показателя естественного прироста (или убыли) населения k. Приведены примеры вычисления названных показателей и использования изменения их значений при анализе сдвигов в демографической ситуации. Рассмотрена демографическая сущность суммарного коэффициента рождаемости , специального коэффициента рождаемости F и даны формулы для их вычислений.