9.2. Модель стабильного населения

Основных теоретических предпосылок или постулат в этой демографической модели также три:

1 - порядок вымирания постоянен и отвечает показателям таблицы дожития;

2 - число рождений изменяется во времени по закону геометрической прогрессии;

3 - внешняя миграция населения отсутствует.

Первая и третья посылка такие же как и в рассмотренной модели стационарного населения. Отличия, и весьма существенные, во втором постулате.

Знаменателем прогрессии, согласно которой изменяются годовые числа рождений, здесь записана экспонента, множитель (?). Суммируя численности всех возрастных групп и вынеся множительза знак суммирования, авторы учебника [2, с. 144] приводят следующее уравнение — формулу получения численностиSстабильного населения:

(21.4)

Не уточнён принцип, на основе которого выведена формула, в том числе, не оговорены различия между двумя, можно сказать «пересеающимися» геометрическими прогрессиями — между и. Но подчеркивается, постулируется, что коэффициентkпо абсолютной величине в том и другом знаменателе одинаковы. В целом вывод этой формулы вызывает сомнение.¹

Далее, на основании уравнение (21.4) авторы полученной формулы для вычисления оценок общих коэффициентов рождаемости nи смертностиm:

(21.5)

Так, как, по мнению авторов, на основании постулата о стабильном населении числитель можно (?) считать равным единице, получаем формулу для коэффициента смертности m:

(21.6)

Представляется малоубедительным и вывод последних двух формул. Согласно формуле (21.5), при постоянном множителе (а он в стабильном населении постоянен), значениеnполучается обратно пропорционально сумме абсолютной численности возрастных групп. Ориентировочные подсчеты показывают, что еслиувеличивается в 10 раз, во столько же раз уменьшаетсяnи наоборот. Таким образом, формулы (21.4)–(21.6) в том виде, в котором они приведены в учебнике [2,c. 144] не пригодны для вычисленийS,n,mстабильного населения.

Следует заметить, что высказанные критические замечания ни малейшим образом не поколебали важность следующих двух утверждений по обсуждаемому вопросу: 1) в стабильном населении соотношения между ежегодным числом рождений его общей численностью — постоянно, следовательно постоянна и величина общего показателя рождаемости; 2) численность возрастных групп и общая численность стабильного населения изменяется по закону геометрической прогрессии прироста (или убыли). При этом, если k< 0, мы получаем убывающий временной ряд численностиS_t, отображающий процесс депопуляции. Примером его является линия дожития, схематически изображающая поло-возрастную пирамиду «в» (рис. 21.1).

На наш взгляд более правильной для вычисления коэффициента рождаемости nбудет следующая формула:

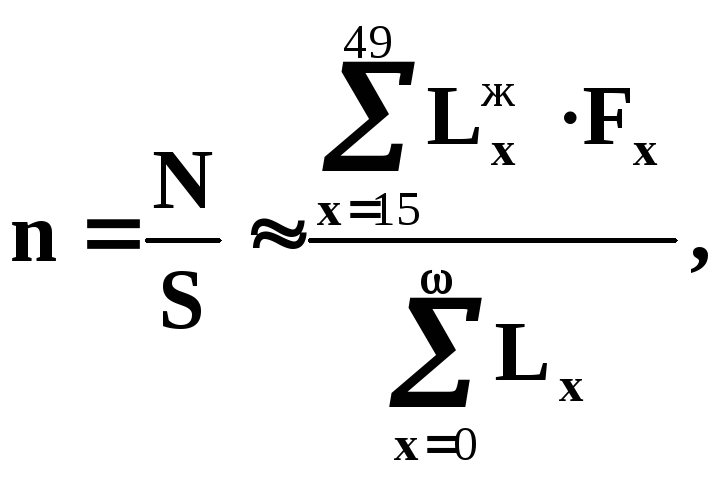(21.7)

где w— максимальный, принятый в таблицах дожития возраст,w= 100 лет.

9.3. Режим воспроизводства и истинный коэффициент естественного прироста населения.

Допустим перед нами стоит следующая демографическая проблема: появились объективные признаки улучшения демографической ситуации, например, во многих регионах, скажем, нашей страны, длительное время страдающей от депопуляции, вдруг коэффициент естественного прироста стал положительным и возросли показатели рождаемости некоторых возрастных групп женщин. Спрашивается, надолго ли удержатся возникшие изменения режима, воспроизводства народонаселения и как оценить устойчивость такого рода сдвигов?

Ответить на эти вопросы можно, вычислив истинный коэффициент естественного приростанаселения (или «коэффициент прогрессивности режима воспроизводства населения» [24,c. 268], которым мы обозначим буквойQи который отвечает тому режиму воспроизводства — замещения поколений, который присущ установившемуся режиму воспроизводства модели стабильного населения при данной совокупности параметров показателей таблицы дожития, таблицы повозрастной плодовитости женщин (F_x) и доле их в составе населения.

Критерием превышения коэффициента kв истинный коэффициентQестественного прироста населения является выполнение следующего правила:

, если (21.8)

где — доля девочек в составе новорожденных,L_x— численность возрастных групп,F_x— средняя плодовитость. В таблице 21.1 дан пример вычисления истинного коэффициента естественного прироста населения.

Таблица 21.1

Расчет истинного коэффициента естественного прироста населения (по данным [2, с. 149])

Возраст, годы, x	k = 0	k = 0,02		k = 0,01		для
						k = 0,005	k = 0,0048	k = 0,0047
15-19	753	0,7047	531	0,8395	632	690	692	694
20-24	3988	0,6376	2543	0,7985	3184	3564	3580	3588
25-29	3087	0,5770	1781	0,7596	2345	2690	2705	2712
30-34	2018	0,5220	1053	0,7225	1458	1715	1727	1732
35-39	1141	0,4724	539	0,6873	784	946	953	957
40-44	340	0,4274	145	0,6538	222	275	277	278
45-49	54	0,3867	21	0,6219	34	43	43	43
	11381		6613		8659	9923	9977	1004
т. е.2*	1,1381		0,6613		0,8659	0,9923	0,9977	1,0004

В таблице показано: взяв k= 0 — получим существенно большую величину суммы, чем требуется правилом (21.8); взявk= 0,02, затемk= 0,01 получаем отклонение в противоположную сторону. Лишь после двух последних «итераций» получаем значениеk, которое с полным правом можно принять заQ— истинный коэффициент естественного прироста населения. Лишь это значениеk, отвечает сложившимся половозрастным соотношениям показателей таблиц дожития и плодовитости. Вычисленноеk=Qотражать будет устойчивый режим воспроизводства поколений в совокупности с приведенной возрастной структурой населения (значениямL_x) и плодовитостью женщин (значениям специальных коэффициентов рождаемостиF_x) будет обеспечивать устойчивый режим воспроизводства населения, реализуя указанные выше свойства модели стабильного населения.

9.4. Истинный коэффициент естественного прироста и коэффициенты воспроизводства населения.

1. Показатели воспроизводства населения. Такого рода показателями в демографии считают: суммарный коэффициент рождаемостиF_, брутто-коэффициент воспроизводстваR_bи нетто-коэффициент воспроизводстваR_n.

Первый и второй показатели рассчитываются без учета данных о смертности женщин и мужчин по формулам:

(21.9)

(21.10)

где n_x– число детей, рожденных 1000 женщин репродуктивного возраста х, или от мужчин аналогичного возраста (коэффициентчаще вычисляется для женщин;— доля девочек среди новорожденных).

При расчете показателей воспроизводства женского и мужского населения одной из областей СССР (данные [1, c. 255]) были получены следующие числа рождений за весь репродуктивный период: для женщин, для мужчин. Подставив эти величины в формулу (21.9), получаем:

.

Следовательно, каждая женщина данного региона за все репродуктивные годы жизни оставила в среднем по 3,25 ребенка, а каждый мужчина — несколько больше, по 3,64.

Брутто-коэффициенты при значении = 0,488 получают таковы:

Таким образом, женщины оставляют после себя женское потомство несколько меньше, чем мужчины — мужское, примерно, на 15%.

Существенный недостаток двух рассмотренных показателей воспроизводства состоит в том, что не учитывается смертность данных таблиц дожития. При вычислении нетто-коэффициента воспроизводства это учтено:

(21.11)

где n_x— число новорожденных, рожденных родителямиx-возраста,L_x— численность возрастных групп;N₀— исходная численность, численность при х = 0 в условном поколении, обычно принимаемая равной 100 000 человек.

В той же таблице [1, с. 256] приводятся следующие значения интересующих нас сумм: ,человек. Исходя из этого получаем:

.

Таким образом, каждая женщина рассматриваемого региона воспроизводит в среднем 1,527 девочекс учетом того, что часть их «не доживает до возраста матери в момент их рождения» (1, с. 257). Имеется ввиду:— это часть контингента дочерей не доживших до возраста своих матерей.

Мужчины оставляют после себя немного больше (примерно на 12%) мальчиков — в среднем по 1,723 мальчика, с учетом того, что часть из них (равная d= 1,864 — 1,723 = 0,141), «не доживает до возраста отца в момент их рождения».

2. Определение коэффициента Q по формуле Лотке. Американский демограф в 1920-е годы предложил для случаев моделей стационарного и стабильного населения определять истинный коэффициент естественного приростаQпо следующей формуле:

(21.12)

где Т — длина женского поколения, т. е. средний возраст женщин при рождении первого ребенка.

Если, как заявили представители российской правящей «элиты», возглавляющие социальную политику страны, действительно они будут добиваться, следуя духу Каирской конференции, чтобы коренное население РФ взяло за правило иметь однодетную семью, т. е. значениеR_nподдерживать на уровне 0,5 деторождений на женщину 15-49-летнего возраста, то чему будет равен коэффициентQнаселения России?

Это путь в историческое небытие. Согласно формуле оценки «демографического тренда» :

(21.13)

здесь _q— время «тренда», изменения численности населения вqраз,kилиQ— коэффициент его естественного прироста (убыли). Численность населения России при сокращении ее каждый год на 2,63% (более чем по 3 млн. человек ежегодно), следовательно, уменьшится на 50% через 26 лет.

Недостатки методов вычисления истинного коэффициента естественного прироста населения Qкак по формуле (21.8), так и по формуле Лотке (21.12) в неучете показателей таблиц смертности, а также приложимость их лишь к моделям стационарного и стабильного населения. Учитывая смертность только возрастных групп женщин с 15 до 49-50 лет. Тогда как в реальности величина коэффициента естественного прироста населения равна разности между годовыми числамиNи всех возрастовM:

k = n — m.

Это равенство по своей сути представляет собой демографическую аксиому, физико-биологическое непреложное требование,которое должно быть выполненным при построениях и выводах любых формул и алгоритмов по статистике населения.

9.5. «Длина» демографических поколений.

Длительность Т или, как принято обозначать в демографии, — «длина» женского и мужского поколения — это отрезок времени, прошедший от дня рождения родителей до дня рождения их дочери или сына.

В современной демографии помимо вычисления средней «длины» поколений Т вычисляют также показатель сосуществования поколений t_T.

1. Вычисление длины поколений.Первый способ — это непосредственное вычисление значений Т^жи Т^мпо данным статистики населения определенного региона. Строится следующая таблица: первая графа — середина семи возрастных групп от 18 до 47 лет, вторая и третья — число детей, родившихся у родителей этих возрастных групп отдельно у женщин и мужчин, четвертая и пятая — число человеко-лет, прожитых отдельно матерями и отцами. Для экономического района, данными о населении которого мы выше пользовались для вычисленийи, в итоговой строке 2-й и 3-й графах рассматриваемой таблицы вписано по 88400 человек (детей), в 4-й графе — 2257000 и в 5-й — 2386600 человеко-лет. На основании этих данных вычисляем интересующие нас показатели:

T^ж= 2 257 000 : 88 400 = 25,5 = 26 лет.

Т^м= 2 386 600 : 88 400 = 26,9 = 27 лет.

Второй способ — вычисление по формуле Лотке, т. е. на основании заданных величин нетто-коэффициента воспроизводства поколений R_nи истинного коэффициента естественного прироста населения подставляемых в следующее равенство:

26 лет,

27 лет.

2. Вычисление показателей сосуществования поколений t_T. В демографии считается наиболее приемлемым способ вычисления показателяt_T, предложенный украинским демографом В. Никитенко (цит. по [1,c. 259]). Он состоит в следующем. В таблице дожития находят показатель ожидаемой продолжительности жизнипри возрастеx₁, соответствующемпоказателю средней длины поколения. Это и будет величина сосуществования двух поколенийt_T:

Если, например T^ж= 26, аT^м= 27, тогда, согласно таблице дожитиягодам — таковы будут и показатели совместного сосуществования ребенка с матерью —и с отцомгода.

Примем, что ожидаемая продолжительность предстоящей жизни для родителей и прародителей такова:

женщины мужчины

родители e₂₆= 51e₂₇= 43

прародители e₅₂= 27e₅₄= 21

прапрародители e₇₈= 9e₈₁= 7 лет

Тогда значения показателей t_Tn, длительностей сосуществования поколений (n= 1, 2, 3) будут следующими:

1) продолжительность сосуществования матери (отца) и дочери (сына):

год, ;

2) продолжительность сосуществования бабушки (дедушки) и внучки (внука):

, ;

3) продолжительность сосуществования прабабушки (прадедушки) и правнучки (правнука) :

, годам.