Кластерный анализ

Метод применяется для разбиения объектов на группы. Типичный пример – группировка покупателей при сегментировании рынка. При разбиении на группы требуется, чтобы внутри группы определенные классификационные признаки были бы схожи, а между группами – различались.

Домашние хозяйства группируются по потреблению энергии, покупатели – по тому, что они ожидают от нового товара, по стилю жизни, население разбивается на гомогенные группы при проведении переписи и анализе ее данных, виды товара – по схожести с товарами конкурентов и т.д. В последние годы кластерный анализ применяется также при исследованиях поведения, отношения и других психологических характеристик.

Пусть стоит задача откомандирования приемщиков грибов и ягод в шесть деревень (A – F)одного района. Если по карте видно, что деревни образуют достаточно тесные группы, то в каждую из таких групп целесообразно послать приемщика. Тогда расстояния, проезжаемые ими при посещении прикрепленных деревень, будут небольшими.

Как нетрудно догадаться, такая идеальная ситуация имеет место далеко не всегда. Во-первых, в средней полосе России деревни обычно располагаются достаточно равномерно. Во-вторых, не всегда соседство на карте означает удобное сообщение. Поэтому следует применять формализованные методы.

Кластерный анализ для рассмотренного примера начинается с определения расстояний между деревнями. Следует определить расстояния между каждой парой деревень¹⁶¹. Полученные результаты имеют вид табл. 5.17.

Таблица 5.17

Расстояния между деревнями, км

DF = 100	AB = 125	AD = 150
DE = 105	BF = 130	CE = 155
AC = 110	CD = 135	BE = 160
BD = 115	EF = 140	AE = 165
BC = 120	CF = 145	AF = 170

Получив расстояния между каждой парой объектов, применяют один из методов кластеризации.

Простая кластеризациязаключается в выполнении следующих шагов:

Шаг 1. Расстояния рассматриваются от минимального до максимального.

Шаг 2. Пару, имеющую минимальное расстояние (максимальное подобие), объединяют в кластер.

Шаг 3.Берется следующее значение расстояния. Если это расстояние между двумя объектами, еще не включенными в кластер, то формируется новый кластер. Если это расстояние между некоторым объектом и одним из членов существующего кластера, то новый объект включается в этот кластер. Если это расстояние между объектами из двух различных кластеров, то эти кластеры объединяются в один.

Простая кластеризация деревень выполняется так, как это показано на рис.Рис. 23 и Рис. 24 ¹⁶². Минимальное расстояние составляет 100. При меньших расстояниях все объекты существуют сами по себе и кластеров нет. На уровне 100 формируется кластер DF (рис.Рис. 23, а). На уровне 105 к нему добавляется объект E (рис.Рис. 23, б). Кластер AC образуется на уровне 110 (рис.Рис. 23, в). Уровень 115 присоединяет объект B к кластеру DEF (рис.Рис. 23, г). Затем, на уровне 120, в результате объединения кластеров AC и BDEF появляется один кластер (рис.Рис. 23, д) и процесс завершается. В данном методе возможно образование кластеров типа цепочек, когда расстояние между соседними объектами будет мало, но некоторые объекты внутри кластера будут находиться далеко друг от друга. В примере один кластер из всех объектов образовался на уровне 120, а расстояние между объектами A и F , входящими в него, составляет 450. Это иллюстрирует особенность простой кластеризации: тенденцию к образованию «цепочек» объектов.

Рис. 23. Ход простой кластеризации

На рис.Рис. 24 ход кластеризации представлен в виде дерева кластеризации (дендрограммы). Это дерево и есть итог процедуры. По нему можно оценить сходство объектов и групп. Например, видно, что кластер DFгораздо более компактный, чем кластерAC. Даже кластерDFE«теснее»AC.

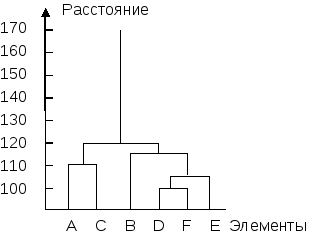
Рис. 24 . Результат простой кластеризации

Полученная дендрограмма может быть использована для следующих действий.

• Выделение компактных групп объектов. Если кластеры объединяются на уровне, значительно бóльшим того, на котором они образуются, то это означает, что имеются компактные группы объектов, далеко отстоящие друг от друга. В данном случае это кластеры ACиDFE. Картину «портит» кластер, состоящий из одного элемента –B. Этот элемент стоит особняком, он далек как от кластераAC, так и от кластераDFE.

• Разделение всех объектов на заданное число групп. Если, например, требуется разбить все деревни на три группы (на большее у фирмы не хватит работников), то выбирается такой уровень, который пересекают три ветви (на рис.Рис. 24 это уровень 112). Далее каждая ветвь дает свой кластер: AC, B и DEF. Именно эти кластеры будут наиболее тесными, и будут отстоять друг от друга на наибольшее расстояние¹⁶³.

Дендрограмма кластеризации с полной связьюпредставлена на рис.Рис. 25. Для объединения в кластер требуется, чтобы расстояние между всеми элементами объединяемых кластеров было не больше заданного уровня.

Вначале населенные пункты DиFобъединяются в один кластер на уровне100. Уровень105пропускается, так как объектEне может быть присоединен к кластеруDF(еще не «проверено» расстояниеEF). Далее формируется кластерAC на уровне110. Уровни115и120пропускаются, так какB еще не может быть присоединен ни к кластеруDF, ни кAC.B добавляется кACтолько на уровне125. Это – расстояние от вновь присоединяемого элементаB досамого дальнего от него элемента клстера AC.Поэтому данный метод кластеризации называется также методомсамого дальнего соседа.

Рис. 25. Кластеризация с полной связью

Следующее подсоединение – объекта E к кластеру DF – происходит на уровне 140. Наконец, один общий кластер образуется на уровне 170 – максимальном расстоянии между исследуемыми объектами.

Этот метод имеет тенденцию к образованию более компактных кластеров. Интересно отметить, что результаты применения двух методов отличаются не только уровнями кластеризации, но и составом кластеров.

Существует также метод кластеризации по среднему расстоянию, когда уровень объединения определяется средним расстоянием между всеми парами объектов из двух объединяемых кластеров. Метод требует большой, хотя и несложной вычислительной работы.

При использовании узловой кластеризациивыбираются, скажем, два объекта, имеющие максимальное расстояние друг от друга. Они образуют полярные узлы – ядра двух кластеров. Остальные объекты присоединяются к тому кластеру, к узлу которого они ближе.

Для кластеризации на заданное число групписпользуется следующий итеративный алгоритм.

Шаг 1.Все объекты случайным образом разбиваются на заданное число кластеров.

Шаг 2.Определяется «центр тяжести» каждого из полученных кластеров.

Шаг 3.Каждый объект переназначается тому кластеру, к центру которого он ближе.

Шаг 4.Процедура повторяется с шага2до тех пор, пока идут перемещения из кластера в кластер¹⁶⁴.

Кластерный анализ может применяться и для группировки объектов не только по расстоянию, но и по другим характериситкам. Возможна и кластеризация по нескольким характеристикам одновременно. Для такой кластеризации следует каким-то образом оценить различие между каждой парой объектов или их подобие¹⁶⁵. Программы, поддерживающие кластерный анализ, работают как с мерами различия, так и с мерами подобия.

Пусть при исследовании покупаемости продукта на рынке требуется исследовать города, в которых он продается. Города описываются двумя характеристиками: X₁– средний доход жителей,X₂– численность населения. Рассмотрим процесс кластеризации для этого случая. Поскольку классификационных переменных только две, можно просто построить пространство с двумя координатами и расположить на нем точки, соответствующие городам. Далее, может быть, будут видны тесные группы. Однако при большем числе переменных требуется использование стандартизированной процедуры. Поскольку применение метода требует довольно значительных вычислений, его развитие шло параллельно с компьютеризацией.

Наиболее часто в качестве меры различия используется евклидово расстояние D_ij между объектами i иj. Для случаяn-мерного пространства оно равно:

где X_ki,X_kj–k-е координаты объектовi иj соответственно¹⁶⁶.

Следует отметить, что это не расстояние в километрах по прямой или по автомобильной дороге. В данном примере в вычисленном расстоянии отражено различие между городами в таких аспектах, как количество жителей и их средний доход. Для схожих по этим двум параметрам городов D_ij будет малó, они будут подобны друг другу. Если города отличаются либо по численности жителей, либо по их доходам, то различие между ними будет больше, а их подобие уменьшится.

После определения таких «расстояний» между каждой парой объектов кластеризация идет по одному из рассмотренных способов.

Итак, результатом кластеризации всегда является рисунок дендрограммы. Интерпретация и использование полученных результатов – дело исследователя. Кластерный анализ – один из ярких примеров того, что математический аппарат дает лишь исходные данные для осмысления их человеком.

Использование кластерного анализа связано с решением следующих проблем.

1.Выбор и кодирование атрибутов. Выбираться должны атрибуты, имеющие концептуальный смысл согласно теории. Кодирование зависит от природы атрибутов. Они могут быть непрерывными величинами (доход), двузначными (пол) или многозначными (район проживания). Тип шкалы может в некоторой степени определяться и исследователем (большая/малая семья или количество человек в семье).

Если кластеризация используется для сегментирования рынка, то их следует выбирать так, чтобы они давали полезные сегменты. Это в первую очередь виды покупаемых товаров; мера удовлетворенности различными характеристиками товарных групп и т. д. Шкалы этих атрибутов чаще номинальные, в лучшем случае – порядковые.

2.Выбор оценки сходства (различия). Для кластеризации необходима некоторая мера расстояния. Евклидово расстояние – далеко не единственная мера. Часто используются меры, основанные на корреляции данных, собранных по каждому элементу исследования. Можно просто взять в качестве меры сходства двух респондентов число товаров, коорые оба предпочитают покупать. Интересные результаты дает мера (D_ij)². Это аналогично выпуклому зеркалу: ближние объекты кажутся еще ближе, а дальние – еще дальше. Например, если имеются три расстояния0,5, 1, 1,5,то их квадраты будут равны0,25, 1, 2,25соответственно.

Сюда же можно отнести и вопрос масштабирования переменных. Например, если мера сходства – евклидово расстояние, и число жителей измеряется в тысячах человек, то в каких единицах измерять доход – в рублях или в тысячах рублей? Во втором случае влияние дохода на сходство и различие будет заметно меньше.

В случаях, когда различные атрибуты отражают данные различной природы или имеют различные шкалы оценки (порядковые и непрерывные), для определения подобия двух объектов, i-го и j-го,используют формулу Гоуэра:

где W_k – вес атрибута; s_ijk – подобие по k-му атрибуту, (k=1,…,m) в диапазоне от 1 (полное подобие) до 0 (полное несоответствие), количественно оцениваемое, например, как

где R_k – диапазон изменения атрибута в выборке (обычно определяется как размах).

В простейшем случае весам присваиваются значения 1(атрибут рассматривается) и0(атрибут не рассматривается). В специальных исследованиях веса определяются исходя из некоторой теории.

Если выбрать все веса равными 1, то это эквивалентно равной значимости всех атрибутов. Если исходно объекты располагаются в пространстве атрибутов внутри эллипсоида (например, размер рассматриваемых городов находится в пределах от50 000до250 000жителей, а доходы колеблются в пределах от1000до30000руб./мес.), то при таком масштабировании все объекты будут расположены внутри сферы.

Если атрибуты двухзначны или многозначны, то для оценки сходства используется коэффициент соответствия – отношение количества совпадающих характеристик к общему их количеству.

Пусть, например, требуется определить сходство читательских вкусов у читателей A,B,Cпо сведениям о читаемых журналах из десяти предложенных. Строится следующая таблица (табл. 5.18).

Таблица 5.18

Оценка читательских вкусов

Пара респондентов	Количество журналов, которые оба читают, a	Количество журналов, которые оба не читают, b	Количество несовпадений во вкусах, c
AB	2	4	4
AC	1	4	5
BC	2	3	5

Подобие читательских вкусов может быть оценено различными способами:

a/(a+b+c); a/(b+c); (a+b)/(a+b+c); b/(a+b+c).

3.Выбор метода кластеризации. Все рассмотренные выше методы – эвристические, то есть «в большинстве случаев работают логично», но не подкреплены никакой теорией. Единственное общее соображение при выборе заключается в том, что методы с усреднением менее чувствительны к ошибкам в исходных данных. Один из способов кластерного анализа – составление дендрограмм различными методами и последующее выделение тех из них, которые имеют простую и полезную содержательную интерпретацию.

Рекомендуется также проводить кластеризацию различными методами и проверять, каие кластеры при этом сохраняются. Такие устойчивые кластеры обычно достойны более пристального внимания.

4.Определение количества и состава итоговых кластеров и их именование.

В заключение следует отметить, что методы кластерного анализа всегда дают какие-то кластеры, даже если в действительности естественных групп объектов и нет.