Chapter 21

Searching

In This Chapter

Performing a sequential search

Performing a binary search

Hashing

Picking a searching algorithm

Searching for data is the second most common activity (after sorting data) necessary for creating many types of programs. A program that stores

names and addresses, for example, needs to sort data and then use a search algorithm to find the data that you want (such as looking for all people who live in Los Angeles and whose last names begin with the letter M ).

To make searching easier, programs usually sort the data first before trying to search it. For more information about sorting, see Chapter 20.

An algorithm is just a fancy way of giving the computer specific types of instructions to accomplish a task. Choosing the right sorting and searching algorithms can make your program run quickly and efficiently. Choose the wrong sorting and searching algorithms and your program may run sluggishly, even for small amounts of data.

Searching Sequentially

A sequential search examines every possible item in a data structure (such as an array or linked list) until it finds what it’s looking for. This type of search is like looking for your car keys in your apartment by going through room

by room, looking in every conceivable location until you find your car keys. Although such a sequential search eventually turns up your car keys (assuming that they’re in your apartment in the first place), it may take a long time.

288 Part V: Algorithms: Telling the Computer What to Do

For small lists, a sequential search is simple to use and fast. But if you need to search large amounts of data, the sequential search bogs down rapidly. Imagine the futility of trying to find your car keys somewhere in the city of New York. That’s the type of task that a sequential search must face in searching through huge amounts of data.

A sequential search can start at either the beginning or the end of a list. It then proceeds to examine every item in the list until it finds the one item that it’s searching for. Then it stops. To see how a sequential search works, try running the following Liberty BASIC program:

MaxSize = 5

REDIM MyArray(MaxSize)

MyArray(1) = INT(RND(1) * 10) + 1

PRINT MyArray(1); SPACE$(1);

FOR I = 2 TO MaxSize

MyArray(I) = MyArray(I - 1) + INT(RND(1) * 10) + 1

PRINT MyArray(I); SPACE$(1);

NEXT I

PRINT

INPUT “Which number do you want to find: “; FindMe

FoundIt = 0

FOR J = 1 TO MaxSize

IF FoundIt = 0 THEN

PRINT “Checking array location “; J

IF MyArray(J) = FindMe THEN

FoundIt = 1

END IF

END IF

NEXT J

IF FoundIt = 1 THEN

PRINT “Found it!”

ELSE

PRINT “The number you want is not in the list.”

END IF

END

This program works as follows:

1.The first and second lines create the variable MaxSize, set the value of MaxSize to 5, and define the array MyArray, which can hold five (the value of MaxSize) integers.

2.The third through ninth lines create a random number and store it in MyArray. Each additional random number is slightly larger than the previous one to create a sorted array of five integers. Then this group of lines prints the complete array on-screen for you to examine.

Chapter 21: Searching 289

3.The tenth line asks the user to type the number to find, which the program stores in the FindMe variable.

4.The eleventh line creates the variable FoundIt and sets its value to 0.

5.The twelfth through nineteenth lines start searching in MyArray for the number that the FindMe variable stores and print each array location that the program checks.

6.The twentieth through twenty-fifth lines print the message Found it! if

the program finds the number; if the program doesn’t find the number, it prints The number that you want is not in the list.

7. The twenty-sixth line marks the end of the program.

One advantage of a sequential search is that you can use it on both sorted and unsorted lists.

Performing a Binary Search

A sequential search starts from the beginning of a list and keeps trudging through the entire list from start to finish until it finds what it’s looking for. But if a list is already sorted, you can shorten the search by using a binary search. (See Chapter 20 for more information about sorting data.)

A binary search divides a long (previously sorted) list in half. If the list that you want to sort contains 10 numbers that it arranges from smallest (on the left) to largest (on the right), the computer looks to see which half of the list (5 numbers on the left and 5 numbers on the right) contains the number for which it’s searching.

Figure 21-1 shows a binary search trying to find the number 37 in a list containing 10 numbers. First, the binary search algorithm cuts the long list in half and examines the number in the middle of the list. Because the list contains 10 numbers, the binary search examines the fifth number in the list. In this case, the middle (fifth) number is 30, which tells the binary search algorithm that the number that it wants (37) must lie in the right half of the list.

Then the binary search takes the right half of the list (consisting of five numbers) and cuts this list in half, which points to the third number in the list (59). Because 59 is larger than 37 (the number that it’s trying to find), the binarysearch algorithm determines that the number 37 must lie in the left side of this part of the list.

The left part of this list contains just two numbers, 37 and 45. With two items in a list, the binary search algorithm needs to look at only the first number in this list, which is 37. Fortunately, 37 is the number that the binary search is looking for, and so the search is over.

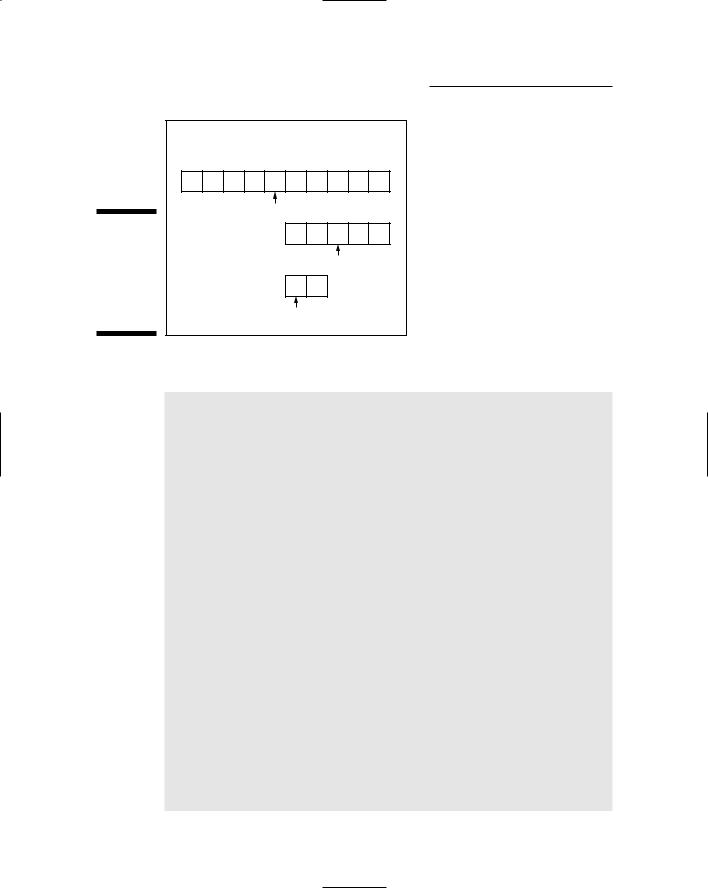
290 Part V: Algorithms: Telling the Computer What to Do

To see how the binary-search algorithm works, try the following program:

MaxSize = 5

REDIM MyArray(MaxSize)

MyArray(1) = INT(RND(1) * 10) + 1

PRINT MyArray(1); SPACE$(1);

FOR I = 2 TO MaxSize

MyArray(I) = MyArray(I - 1) + INT(RND(1) * 10) + 1

PRINT MyArray(I); SPACE$(1);

NEXT I

PRINT

INPUT “Which number do you want to find: “; FindMe

Left = 1

Right = MaxSize

Time2Stop = 0

WHILE Time2Stop = 0

Half = INT((Left + Right) / 2)

IF FindMe < MyArray(Half) THEN

Right = Half - 1

ELSE

Left = Half + 1

END IF

IF (FindMe = MyArray(Half) OR Left > Right) THEN

Time2Stop = 1

END IF

WEND

IF FindMe = MyArray(Half) THEN

PRINT “Found it in location “; Half

ELSE

PRINT “The number you want is not in the list.”

END IF

END

Chapter 21: Searching 291

The binary search program works as follows:

1.The first and second lines create the variable MaxSize, set the value of MaxSize to five, and define the array MyArray, which can hold five integers (the value of MaxSize).

2.The third through ninth lines create a random number and store it in MyArray. Each additional random number is slightly larger than the previous one to create a sorted array of five integers. Then this group of lines prints the complete array on-screen for you to examine.

3.The tenth line asks the user to type the number to find which the program stores in the FindMe variable.

4.The eleventh line creates the variable Left and sets its value to 1.

5.The twelfth line creates the variable Right and sets its value to MaxSize, the maximum size of the array.

6.The thirteenth line creates the variable Time2Stop and sets its value to 0.

7.The fourteenth line is the start of a WHILE WEND loop that repeats until the binary search finds the FindMe number in the array or until it searches the entire array and can’t find the FindMe number.

8.The fifteenth line creates the variable Half, which divides the list in half and stores the integer result. (So if you divide an odd number, the integer result drops all fractions, so INT(5 / 2) equals 2.)

9.The sixteenth through twentieth lines look for the FindMe number in the left half of the array. If the FindMe number is less than the item that the middle of the array stores, the Right variable is set to Half - 1. Otherwise, the value of the Left variable is set to Half + 1. By lowering the value of the Right variable and increasing the value of the Left variable, the program can keep track after it searches all numbers in the array without finding the number that it’s looking for. The moment that the Left variable becomes greater than the Right variable, the program knows that the number it’s searching for isn’t anywhere in the array.

10.The twenty-first through twenty-third lines check to see whether it can find the FindMe number or until the program determines that the FindMe number doesn’t exist. If this situation occurs, the value of the Time2Stop variable is set to 1.

11.The twenty-fourth line marks the end of the WHILE-WEND loop.

12.The twenty-fifth through twenty-ninth lines print the message Found it in location, following that message with the array position. If it doesn’t find the number in the array, the program prints The number that you want is not in the list.

13.The thirtieth line marks the end of the program.