Beginning Algorithms (2006)

Chapter 18

How It Works

The preceding test cases work by considering many examples of lines that may or may not intersect, and may or may not be vertical. When using tests to drive the implementation, it is important to cover all such cases and not just assume that the cases are covered. It may seem like a lot of test cases, but remember that you are testing for a lot of behaviors. If you require many more tests than this, you should think of ways to break up the functionality into multiple classes. This is actually why the Slope class was created!

In the next Try It Out, you implement the Line class itself and pass these tests.

The Line class has three instance members: the two Point objects that define its end-points, and a Slope object to encapsulate its slope. Create the fields and constructor as shown here:

package com.wrox.algorithms.geometry;

public class Line { private final Point _p; private final Point _q;

private final Slope _slope;

public Line(Point p, Point q) {

assert p != null : “point defining a line cannot be null”; assert q != null : “point defining a line cannot be null”;

_p = p; _q = q;

_slope = new Slope(_p.getY() - _q.getY(), _p.getX() - _q.getX());

}

...

}

You implement the isParallelTo() method by relying on the Slope’s ability to determine whether it is equal to another Slope:

public boolean isParallelTo(Line line) { return _slope.equals(line._slope);

}

Implement the contains() method to determine whether a line contains the supplied point:

public boolean contains(Point a) {

if (!isWithin(a.getX(), _p.getX(), _q.getX())) { return false;

}

if (!isWithin(a.getY(), _p.getY(), _q.getY())) { return false;

}

if (_slope.isVertical()) { return true;

454

Computational Geometry

}

return a.getY() == solveY(a.getX());

}

Create a method to calculate the y coordinate of a point on the line, given the x coordinate:

private double solveY(double x) {

return _slope.asDouble() * x + base();

}

You also create a method to determine the value of b in the formula y = mx + b:

private double base() {

return _p.getY() - _slope.asDouble() * _p.getX();

}

Create a simple utility to determine whether one number is within the range specified by two other numbers:

private static boolean isWithin(double test, double bound1, double bound2) { return test >= Math.min(bound1, bound2)

&& test <= Math.max(bound1, bound2);

}

Now you create the method that determines the intersection point of two lines:

public Point intersectionPoint(Line line) { if (isParallelTo(line)) {

return null;

}

double x = getIntersectionXCoordinate(line); double y = getIntersectionYCoordinate(line, x);

Point p = new Point(x, y);

if (line.contains(p) && this.contains(p)) { return p;

}

return null;

}

To support the preceding code, create a method to determine the x coordinate of the theoretical point of intersection of the two lines:

private double getIntersectionXCoordinate(Line line) { if (_slope.isVertical()) {

return _p.getX();

}

if (line._slope.isVertical()) {

455

Chapter 18

return line._p.getX();

}

double m = _slope.asDouble(); double b = base();

double n = line._slope.asDouble(); double c = line.base();

return (c - b) / (m - n);

}

Finally, create a method to determine the y coordinate of the point of intersection:

private double getIntersectionYCoordinate(Line line, double x) { if (_slope.isVertical()) {

return line.solveY(x);

}

return solveY(x);

}

How It Works

The Line class has three instance members: the two Point objects that define its end-points, and a Slope object to encapsulate its slope. Much of the functionality of the Line class is actually provided by these encapsulated member objects. For example, to determine whether a line is parallel to another line, you simply need to determine whether their respective slopes are equal.

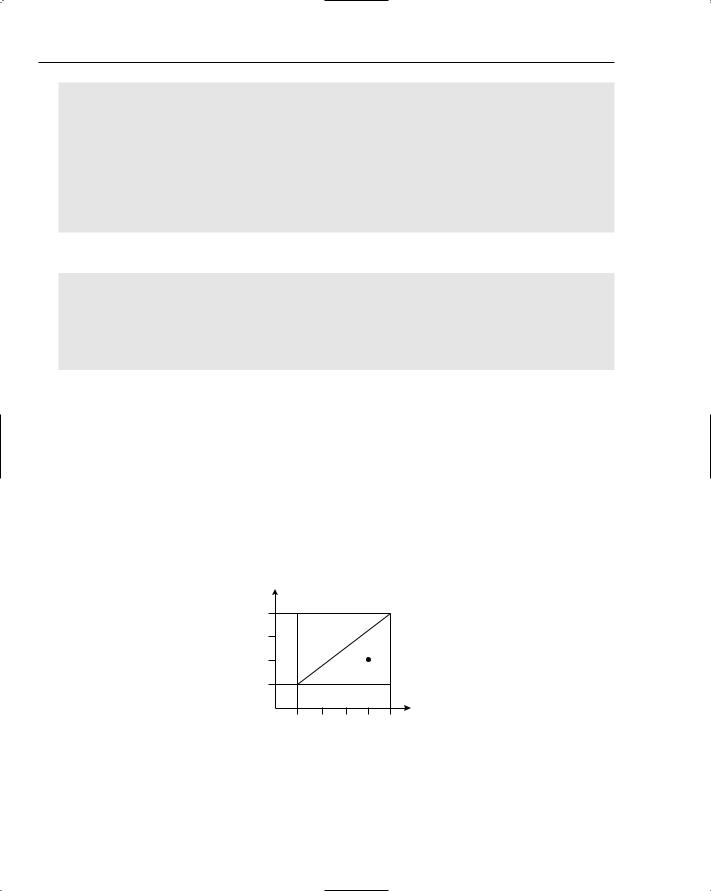
To determine whether a point falls within a line, you see whether the point’s x coordinate falls within the range of x coordinates defined by its end-points. If not, you know the line cannot possibly contain the point. You then repeat the process for the y coordinate span of the line. Having made it that far, you know that the point in question is a candidate for being on the line. In fact, if the line is vertical, you can conclude that the point is actually on the line. However, consider Figure 18-14, which shows a point that has passed all of these tests but is still not on the line.

Figure 18-14: A point that is not part of the line, but which has x and y coordinates within the span of the line.

You have to do a final check to determine whether this point’s coordinates make sense when plugged into the formula for the line (y = mx + b). For this, you create a call to solveY(). Given a value for the

456

Computational Geometry

x coordinate, it calculates the corresponding y coordinate. If the point’s coordinates evaluate correctly, the point lies on the line.

Now you come to the heart of the matter: determining the intersection point of two lines. The basic idea is this: If the lines are parallel, there is no intersection point; if they aren’t, first determine the x coordinate of the (theoretical) intersection point, and then use this value to determine the y coordinate of the (theoretical) intersection point. Finally, you need to confirm that both lines actually contain the theoretical intersection point before returning it.

To determine the x coordinate of the intersection point, you first need to determine whether either line in question is vertical. If one is, the answer is just the x coordinate of either end-point of the vertical line. If not, you use the formula described earlier to determine the x coordinate of the intersection point.

The final method determines the y coordinate of the point of intersection. Again, you have to be on guard for the case where one of the lines is vertical (you won’t be doing this if both are vertical). This means that you simply use a nonvertical line to calculate the y coordinate of the point of intersection.

If you run the tests, you will see that all of them work. You now have a nicely abstracted set of classes representing geometrical concepts, with some well-tested and valuable functionality. You can now move on to your next challenge, finding the closest pair among an arbitrary set of points.

Finding the Closest Pair of Points

Imagine a large set of scattered points such as those shown in Figure 18-15.

Figure 18-15: A number of scattered points.

Can you find the pair of points that are closest to each other? You might think that’s pretty easy — just compare every point with every other point, compute the distance between them, and remember the pair of points with the minimum distance. While that would work, by now you should be forming an allergy to brute-force solutions that are O(N2) because they process every item in relation to every other item. We won’t bother implementing such a naive solution for this problem. Instead, this section looks at an algorithm known as the plane sweep algorithm.

457

Chapter 18

The plane sweep algorithm considers each point in order from left to right in the coordinate system. It makes a single pass, or sweep, across the two-dimensional plane containing the points, remembering the currently known smallest distance and the two points that are separated by that minimum distance.

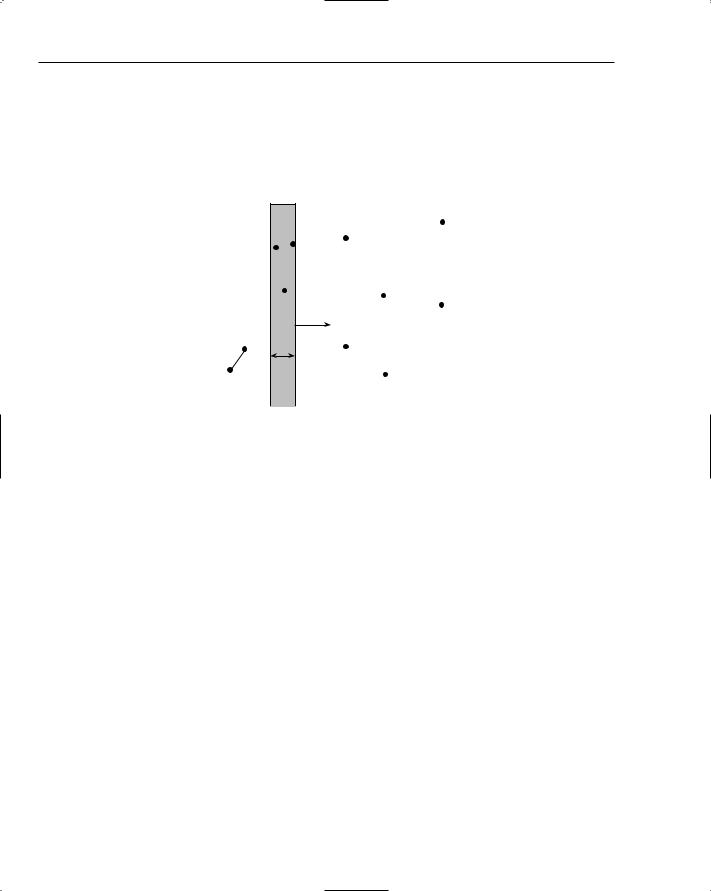
It’s easier to understand this algorithm with an example that has progressed a little. Figure 18-16 shows the state of the algorithm when the fifth point (from left to right) is about to be processed (the x and y axes have been removed to avoid cluttering the diagram).

Sweep direction

d

d

Drag

net

Figure 18-16: The plane sweep algorithm in progress.

Notice in the figure that the currently identified closest pair of points is separated by a distance d. The point currently being considered as the sweep progresses is treated as if it was at the right edge of a r ectangular box referred to as the drag net. The key thing to notice about the drag net is that its width is also d — that is, you create an imaginary box behind the current point that is no wider than the distance between the current closest pair of points. That’s quite a mouthful, but it will make sense soon enough.

The idea is that if the point being considered is to be part of a pair (with a point to its left) that is a closer pair than the current closest pair, then the second point in that new pair must lie within the drag net.

If not, it could hardly form a closer pair than the currently identified pair. Therefore, the algorithm checks the distance between the point under the sweep line with all other points in the drag net to determine whether any combination forms a closer pair than the one currently identified. If a closer pair is found, the algorithm proceeds with a smaller drag net until every point has been processed. In this way, depending on the distribution of the points, relatively few comparisons are required. A more advanced form of the algorithm can ignore points in the drag net that are farther away than d from the point being considered in the y direction as well, restricting the number of comparisons even further.

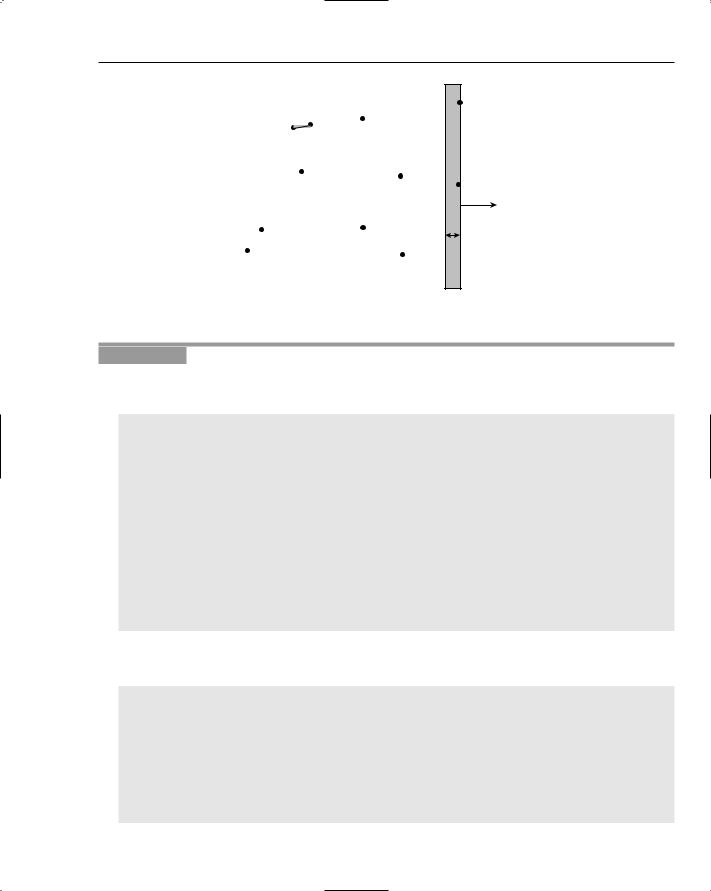
Figure 18-17 shows the situation after almost all the points have been processed.

There are two main aspects to implementing the plane sweep algorithm just described. The points need to be sorted according to their coordinates, and then they have to be scanned in the algorithm itself. The first thing you need to be able to do is sort the points into logical order. This involves creating a comparator that can be plugged into a sorting algorithm. In the following Try It Out, you write tests for this comparator.

458

Computational Geometry

d

Sweep direction

d

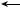Drag

net

Figure 18-17: The algorithm is almost complete.

You start with a simple test that proves that two points that are equal are correctly handled by our comparator — that is, the result is zero:

package com.wrox.algorithms.geometry;

import junit.framework.TestCase;

public class XYPointComparatorTest extends TestCase {

private final XYPointComparator _comparator = XYPointComparator.INSTANCE;

public void testEqualPointsCompareCorrectly() {

Point p = new Point(4, 4);

Point q = new Point(4, 4);

assertEquals(0, _comparator.compare(p, q)); assertEquals(0, _comparator.compare(p, p));

}

...

}

You then need a test to prove that the points sort according to their x coordinate as you expect. You do this by setting up three points and testing them relative to each other, as shown here:

public void testXCoordinateIsPrimaryKey() { Point p = new Point(-1, 4);

Point q = new Point(0, 4); Point r = new Point(1, 4);

assertEquals(-1, _comparator.compare(p, q)); assertEquals(-1, _comparator.compare(p, r)); assertEquals(-1, _comparator.compare(q, r));

assertEquals(1, _comparator.compare(q, p));

459

Chapter 18

assertEquals(1, _comparator.compare(r, p)); assertEquals(1, _comparator.compare(r, q));

}

Finally, you need a test to establish that the points will take their y coordinates into account when their x coordinates are the same. Here’s the code for this test:

public void testYCoordinateIsSecondaryKey() { Point p = new Point(4, -1);

Point q = new Point(4, 0); Point r = new Point(4, 1);

assertEquals(-1, _comparator.compare(p, q)); assertEquals(-1, _comparator.compare(p, r)); assertEquals(-1, _comparator.compare(q, r));

assertEquals(1, _comparator.compare(q, p)); assertEquals(1, _comparator.compare(r, p)); assertEquals(1, _comparator.compare(r, q));

}

How It Works

You need a comparator that can sort points according to their x coordinates. This obviously means that negative x coordinates will precede positive ones, but what about when two points share the same x coordinate? You need to sort them somehow, so you arbitrarily choose to sort them by their y coordinate in this circumstance. You might be wondering how to handle points that have the same x and y coordinates. The answer is that you won’t allow that — by simply using a Set to contain the points under consideration. Recall that the semantics of a Set do not allow duplicate items, and that Point objects are considered equal if both their coordinates are the same.

The immediately previous tests work by creating a sufficiently broad set of cases and asserting that the comparator provides the expected behavior. That should be enough to get your comparator going. You implement it in the next Try It Out.

Start by declaring a singleton instance and a private constructor, as this object has no state of its own:

package com.wrox.algorithms.geometry;

import com.wrox.algorithms.sorting.Comparator;

public final class XYPointComparator implements Comparator {

public static final XYPointComparator INSTANCE = new XYPointComparator();

private XYPointComparator() {

}

...

}

460

Computational Geometry

Implement compare(), which delegates to a strongly typed version by casting its parameters to Point objects:

public int compare(Object left, Object right) throws ClassCastException { return compare((Point) left, (Point) right);

}

Finally, create the strongly typed version of compare():

public int compare(Point p, Point q) throws ClassCastException {

int result = new Double(p.getX()).compareTo(new Double(q.getX())); if (result != 0) {

return result;

}

return new Double(p.getY()).compareTo(new Double(q.getY()));

}

How It Works

Don’t be concerned that the comparator itself takes fewer lines of code than the accompanying unit test — it’s perfectly normal! The only method you need to implement is compare(), which delegates to a strongly typed version by casting its parameters to Point objects. This will throw a ClassCastException when objects other than points are passed in, but that is explicitly allowed by the Comparator interface.

The implementation of the compare() method, which knows the objects are of class Point, is where the real logic lives. The return value is based on the x coordinates of the respective objects, and only if they are equal does the method take their y coordinates into account.

With your comparator in place, you are ready to implement the plane sweep algorithm itself, which you do in the next Try It Out. You assume that there will be other algorithms that solve the problem of finding the closest pair (see the exercises at the end of this chapter), so you create an abstract test that can be used to prove the behavior of various implementations. You then extend this test with a specific version for our algorithm.

Define an abstract factory method to allow specific implementations to instantiate the appropriate algorithm class, as shown here:

package com.wrox.algorithms.geometry;

import com.wrox.algorithms.sets.ListSet; import com.wrox.algorithms.sets.Set; import junit.framework.TestCase;

public abstract class AbstractClosestPairFinderTestCase extends TestCase { protected abstract ClosestPairFinder createClosestPairFinder();

...

}

461

Chapter 18

The first test case simply proves that if you supply an empty set of points, you get null in return:

public void testEmptySetOfPoints() {

ClosestPairFinder finder = createClosestPairFinder();

assertNull(finder.findClosestPair(new ListSet()));

}

It’s pretty hard to find the closest pair when there’s only a single point, so you also prove that in this case you get null as a return value:

public void testASinglePointReturnsNull() { ClosestPairFinder finder = createClosestPairFinder();

Set points = new ListSet();

points.add(new Point(1, 1));

assertNull(finder.findClosestPair(points));

}

Obviously, the next case occurs when only two points are provided in the input set. In this case, it’s easy to determine the closest pair, so test it with the following code:

public void testASinglePairOfPoints() { ClosestPairFinder finder = createClosestPairFinder();

Set points = new ListSet();

Point p = new Point(1, 1);

Point q = new Point(2, 4);

points.add(p);

points.add(q);

Set pair = finder.findClosestPair(points);

assertNotNull(pair); assertEquals(2, pair.size()); assertTrue(pair.contains(p)); assertTrue(pair.contains(q));

}

Now we come to an interesting case. Imagine there are three points in a line, evenly spaced. Which pair should be the closest pair? You’d like your algorithm to take the first pair it encounters in the sweep, which will depend on the comparator you created to sort the points. You need to make sure this is what happens, so here is the test:

public void testThreePointsEquallySpacedApart() { ClosestPairFinder finder = createClosestPairFinder();

Set points = new ListSet();

Point p = new Point(1, 0);

Point q = new Point(1, 4);

462

Computational Geometry

Point r = new Point(1, -4);

points.add(p);

points.add(q);

points.add(r);

Set pair = finder.findClosestPair(points);

assertNotNull(pair); assertEquals(2, pair.size()); assertTrue(pair.contains(p)); assertTrue(pair.contains(r));

}

A similar case occurs when you have a larger set of points in which two pairs have the same distance. Again, you decide you want the algorithm to return the pair it encounters first, so you prove it with the following test case:

public void testLargeSetOfPointsWithTwoEqualShortestPairs() { ClosestPairFinder finder = createClosestPairFinder();

Set points = new ListSet();

points.add(new Point(0, 0)); points.add(new Point(4, -2)); points.add(new Point(2, 7)); points.add(new Point(3, 7)); points.add(new Point(-1, -5)); points.add(new Point(-5, 3));

points.add(new Point(-5, 4)); points.add(new Point(-0, -9)); points.add(new Point(-2, -2));

Set pair = finder.findClosestPair(points);

assertNotNull(pair); assertEquals(2, pair.size());

assertTrue(pair.contains(new Point(-5, 3))); assertTrue(pair.contains(new Point(-5, 4)));

}

Finally, you extend your abstract test case, making a version that is specific to your plane sweep algorithm, as shown here:

package com.wrox.algorithms.geometry;

public class PlaneSweepClosestPairFinderTest extends AbstractClosestPairFinderTestCase {

protected ClosestPairFinder createClosestPairFinder() { return PlaneSweepClosestPairFinder.INSTANCE;

}

}

463