Beginning Algorithms (2006)

Chapter 18

This means that if you know the formulas for the two lines, you can find the x coordinate of the point of intersection by the formula just shown. In this example, the formula would be as follows:

x = (–2 – 2) / (0.5 – –2)

This becomes the following:

x = –4 / 2.5

Or it becomes the following:

x = –1.6

If you refer to Figure 18-12, this looks about right for the x coordinate of the point of intersection. Figuring out the y coordinate is trivial; put the just discovered x coordinate back into the formula for either line. For example:

y = 0.5x + 2

y = 0.5 × –1.6 + 2

y = –0.8 + 2

y = 1.2

The point of intersection is therefore (–1.6, 1.2) for the example lines.

The method varies slightly when one of the lines is vertical. The steps to find the x coordinate of the point of intersection do not apply, because the x coordinate of the point of intersection when one of the lines is vertical will simply be the x coordinate of the vertical line itself. Solving the nonvertical line’s equation for this value of x will finish the job. It’s now time to put all the theory discussed in the previous sections to work in some code. In the following Try It Out exercise, many of the concepts map directly to objects in Java, so the effort spent getting the concepts clear is worthwhile. You will begin by creating a class to represent points.

Start by defining what you want the Point class to do in the form of a JUnit test case. You only need two behaviors from Point: to determine whether a point is the same as another (that is, it has the same coordinates), and to determine the distance from one point to another.

Here is the code:

package com.wrox.algorithms.geometry;

import junit.framework.TestCase;

public class PointTest extends TestCase { public void testEquals() {

assertEquals(new Point(0, 0), new Point(0, 0));

444

Computational Geometry

assertEquals(new Point(5, 8), new Point(5, 8)); assertEquals(new Point(-4, 6), new Point(-4, 6));

assertFalse(new Point(0, 0).equals(new Point(1, 0))); assertFalse(new Point(0, 0).equals(new Point(0, 1))); assertFalse(new Point(4, 4).equals(new Point(-4, 4))); assertFalse(new Point(4, 4).equals(new Point(4, -4))); assertFalse(new Point(4, 4).equals(new Point(-4, -4))); assertFalse(new Point(-4, 4).equals(new Point(-4, -4)));

}

public void testDistance() {

assertEquals(13d, new Point(0, 0).distance(new Point(0, 13)), 0); assertEquals(13d, new Point(0, 0).distance(new Point(13, 0)), 0); assertEquals(13d, new Point(0, 0).distance(new Point(0, -13)), 0); assertEquals(13d, new Point(0, 0).distance(new Point(-13, 0)), 0);

assertEquals(5d, new Point(1, 1).distance(new Point(4, 5)), 0); assertEquals(5d, new Point(1, 1).distance(new Point(-2, -3)), 0);

}

}

To begin the implementation of Point, declare an instance variable to hold each of the x and y coordinates, and a constructor to initialize them. Note that both fields are final, making objects of this class immutable:

package com.wrox.algorithms.geometry;

public class Point { private final double _x; private final double _y;

public Point(double x, double y) { _x = x;

_y = y;

}

...

}

Then provide simple accessors for the coordinates:

public double getX() { return _x;

}

public double getY() { return _y;

}

Use Pythagoras’ theorem to calculate the distance between this point and another supplied to the distance() method:

445

Chapter 18

public double distance(Point other) {

assert other != null : “other can’t be null”;

double rise = getY() - other.getY();

double travel = getX() - other.getX();

return Math.sqrt(rise * rise + travel * travel);

}

All that is left is to implement equals() and hashCode(), as follows:

public int hashCode() { return (int) (_x * _y);

}

public boolean equals(Object obj) { if (this == obj) {

return true;

}

if (obj == null || obj.getClass() != getClass()) { return false;

}

Point other = (Point) obj;

return getX() == other.getX() && getY() == other.getY();

}

How It Works

The Point class holds a value for each of its x and y coordinates as member variables. These variables are initialized in the constructor and cannot be changed. To determine the distance from a point to another point, the code treats the two points as the corners of a right-angled triangle, using Pythagoras’ theorem to determine the length of the hypotenuse of the triangle, which is the distance between the points.

The code also determines whether two points are equal. All that is required for two points to be considered equal is that they have matching coordinates, so the code simply compares the x and y coordinates of the two points and returns true if they are both the same.

That’s all there is to the Point class. In the next Try It Out, you model the slope of a line.

Begin by writing a test case that proves a slope knows when it’s vertical:

package com.wrox.algorithms.geometry;

import junit.framework.TestCase;

public class SlopeTest extends TestCase { public void testIsVertical() {

assertTrue(new Slope(4, 0).isVertical());

446

Computational Geometry

assertTrue(new Slope(0, 0).isVertical()); assertTrue(new Slope(-5, 0).isVertical()); assertFalse(new Slope(0, 5).isVertical()); assertFalse(new Slope(0, -5).isVertical());

}

...

}

Next you create a test to prove that a slope can determine whether it is parallel to another slope. Use the standard equals() method for this:

public void testEquals() {

assertTrue(new Slope(0, -5).equals(new Slope(0, 10))); assertTrue(new Slope(1, 3).equals(new Slope(2, 6))); assertFalse(new Slope(1, 3).equals(new Slope(-1, 3))); assertFalse(new Slope(1, 3).equals(new Slope(1, -3))); assertTrue(new Slope(5, 0).equals(new Slope(9, 0)));

}

Create a test method to ensure that a nonvertical slope can calculate its value as a Java double:

public void testAsDoubleForNonVerticalSlope() { assertEquals(0, new Slope(0, 4).asDouble(), 0); assertEquals(0, new Slope(0, -4).asDouble(), 0); assertEquals(1, new Slope(3, 3).asDouble(), 0); assertEquals(1, new Slope(-3, -3).asDouble(), 0);

assertEquals(-1, new Slope(3, -3).asDouble(), 0); assertEquals(-1, new Slope(-3, 3).asDouble(), 0); assertEquals(2, new Slope(6, 3).asDouble(), 0); assertEquals(1.5, new Slope(6, 4).asDouble(), 0);

}

Finally, you need to verify what happens were someone silly enough to try to calculate the slope of a vertical line as a double value. You make sure that an exception is thrown with an appropriate message:

public void testAsDoubleFailsForVerticalSlope() { try {

new Slope(4, 0).asDouble(); fail(“should have blown up!”);

} catch (IllegalStateException e) {

assertEquals(“Vertical slope cannot be represented as double”, e.getMessage());

}

}

How It Works

The code assumes that a Slope object can be instantiated by providing two integer values that describe the rise and travel of the slope. It is important to remember that this does not represent a fixed point in two-dimensional space. Likewise, a slope does not have a length either. You are purely interested in representing only the slope itself. Many lines between different points can share the same slope. Lines that share the same slope are parallel. This is represented in the code by the test that proves that a slope can determine whether it is equal to another slope. This is achieved by providing both positive and negative test cases to ensure that the implementation is robust.

447

Chapter 18

Recall from the description of the formula of a line (y = mx + b) that the value m is a floating-point value that is the ratio of the rise of the line to its travel. The preceding test code provides several assertions to establish that the implementation can correctly calculate this value. You need to separate the tests that deal with vertical lines from those that deal with nonvertical lines, as attempting to calculate this value for a vertical line is impossible; the tests prove that trying to do so will raise an exception.

Passing this set of tests will give you a robust implementation, so we’ll build that in the next Try It Out.

Begin the slope implementation with the pair of final member variables and a constructor to initialize them, as shown here:

package com.wrox.algorithms.geometry;

public class Slope {

private final double _rise; private final double _travel;

public Slope(double rise, double travel) { _rise = rise;

_travel = travel;

}

...

}

Implement isVertical(), which is trivial indeed:

public boolean isVertical() { return _travel == 0;

}

Implement hashCode() and equals() to determine whether two slopes are the same:

public int hashCode() {

return (int) (_rise * _travel);

}

public boolean equals(Object object) { if (this == object) {

return true;

}

if (object == null || object.getClass() != getClass()) {

return false;

}

Slope other = (Slope) object;

if (isVertical() && other.isVertical()) { return true;

}

if (isVertical() || other.isVertical()) {

448

Computational Geometry

return false;

}

return (asDouble()) == (other.asDouble());

}

Finally, you calculate the numerical representation of the slope, being careful to avoid vertical lines:

public double asDouble() { if (isVertical()) {

throw new IllegalStateException(“Vertical slope cannot be represented

as double”);

}

return _rise / _travel;

}

How It Works

You have previously seen classes that have member variables that are final and are initialized in the constructor like the Slope class just described, so the basic structure of the class should be familiar.

Determining whether two slopes are equal is a little more challenging. You implement a simple hashCode() and then build the equals() implementation with three cases in mind: first is the case when both slopes are vertical, in which case they are equal; next is the case when one of the slopes is vertical, in which case they are not equal. Finally is the general case, in which two slopes are equal if their representation as a Java double ratio is the same. The code has to eliminate all cases involving vertical slopes before attempting to calculate the numerical representation of either slope.

The final method calculates the ratio of the slope’s rise to its travel as a double value. The only trick is to avoid dividing by zero when the slope is vertical. The code deals with this issue by throwing an exception.

In the next Try It Out, you set up the tests to determine several qualities of a line, including whether a given point falls on it, whether it is vertical or parallel to another line, and so on.

The final class in the line intersection problem is Line. You begin by writing a series of test cases to define the functionality you want Line to provide. Start with a test that proves you can ask Line whether it contains a specified Point — that is, whether Point falls on the line:

package com.wrox.algorithms.geometry;

import junit.framework.TestCase;

public class LineTest extends TestCase {

public void testContainsForNonVerticalLine() {

Point p = new Point(0, 0);

Point q = new Point(3, 3);

Line l = new Line(p, q);

assertTrue(l.contains(p));

449

Chapter 18

assertTrue(l.contains(q));

assertTrue(l.contains(new Point(1, 1))); assertTrue(l.contains(new Point(2, 2))); assertTrue(l.contains(new Point(0.5, 0.5)));

assertFalse(l.contains(new Point(3.1, 3.1))); assertFalse(l.contains(new Point(3, 3.1))); assertFalse(l.contains(new Point(0, 1))); assertFalse(l.contains(new Point(-1, -1)));

}

...

}

You separately test the functionality for a vertical line, just to make sure that the special case is covered, as shown here:

public void testContainsForVerticalLine() { Point p = new Point(0, 0);

Point q = new Point(0, 3);

Line l = new Line(p, q);

assertTrue(l.contains(p));

assertTrue(l.contains(q));

assertTrue(l.contains(new Point(0, 1))); assertTrue(l.contains(new Point(0, 2))); assertTrue(l.contains(new Point(0, 0.5)));

assertFalse(l.contains(new Point(0, 3.1))); assertFalse(l.contains(new Point(0.1, 1))); assertFalse(l.contains(new Point(1, 0))); assertFalse(l.contains(new Point(-1, -1)));

}

You want a line to indicate whether it is parallel to another line. You need to be careful and treat vertical lines as a special case. The first test proves the correct behavior when the two lines are parallel but not vertical:

public void testIsParallelForTwoNonVerticalParallelLines() { Point p = new Point(1, 1);

Point q = new Point(6, 6); Point r = new Point(4, -2); Point s = new Point(6, 0);

Line l = new Line(p, q);

Line m = new Line(r, s);

assertTrue(l.isParallelTo(m));

assertTrue(m.isParallelTo(l));

}

450

Computational Geometry

Next, you test the behavior for two nonvertical and nonparallel lines:

public void testIsParallelForTwoNonVerticalNonParallelLines() { Point p = new Point(1, 1);

Point q = new Point(6, 4); Point r = new Point(4, -2); Point s = new Point(6, 0);

Line l = new Line(p, q);

Line m = new Line(r, s);

assertFalse(l.isParallelTo(m));

assertFalse(m.isParallelTo(l));

}

In the following test, you address some of the edge cases — first, when both lines are vertical (and therefore by definition parallel):

public void testIsParallelForTwoVerticalParallelLines() { Point p = new Point(1, 1);

Point q = new Point(1, 6); Point r = new Point(4, -2); Point s = new Point(4, 0);

Line l = new Line(p, q);

Line m = new Line(r, s);

assertTrue(l.isParallelTo(m));

assertTrue(m.isParallelTo(l));

}

The final test of the isParallel() method is for the case when one of the lines is vertical and the other is not:

public void testIsParallelForOneVerticalAndOneNonVerticalLine() { Point p = new Point(1, 1);

Point q = new Point(1, 6); Point r = new Point(4, -2); Point s = new Point(6, 0);

Line l = new Line(p, q);

Line m = new Line(r, s);

assertFalse(l.isParallelTo(m));

assertFalse(m.isParallelTo(l));

}

Now you define some tests for determining the point of intersection of two lines. You create a method on Line called intersectionPoint() that will be passed another Line object. This method will be allowed to return null if the lines do not intersect, or a Point object that defines the point of intersection if they do. Again, you need to take extra care to cover cases involving vertical lines.

451

Chapter 18

First prove that two nonvertical lines that are parallel are correctly determined to have no intersection, as shown in the following test method:

public void testParallelNonVerticalLinesDoNotIntersect() { Point p = new Point(0, 0);

Point q = new Point(3, 3); Point r = new Point(5, 0); Point s = new Point(8, 3);

Line l = new Line(p, q);

Line m = new Line(r, s);

assertNull(l.intersectionPoint(m));

assertNull(m.intersectionPoint(l));

}

Now establish the same behavior for a pair of vertical lines:

public void testVerticalLinesDoNotIntersect() { Point p = new Point(0, 0);

Point q = new Point(0, 3); Point r = new Point(5, 0); Point s = new Point(5, 3);

Line l = new Line(p, q);

Line m = new Line(r, s);

assertNull(l.intersectionPoint(m));

assertNull(m.intersectionPoint(l));

}

Now test a case in which the two lines do have an easily determined point of intersection and prove that it works as expected:

public void testIntersectionOfNonParallelNonVerticalLines() { Point p = new Point(0, 0);

Point q = new Point(4, 4); Point r = new Point(4, 0); Point s = new Point(0, 4);

Line l = new Line(p, q);

Line m = new Line(r, s);

Point i = new Point(2, 2);

assertEquals(i, l.intersectionPoint(m)); assertEquals(i, m.intersectionPoint(l));

}

Next cover the case in which one of the lines is vertical, as shown here:

452

Computational Geometry

public void testIntersectionOfVerticalAndNonVerticalLines() { Point p = new Point(0, 0);

Point q = new Point(4, 4); Point r = new Point(2, 0); Point s = new Point(2, 4);

Line l = new Line(p, q);

Line m = new Line(r, s);

Point i = new Point(2, 2);

assertEquals(i, l.intersectionPoint(m)); assertEquals(i, m.intersectionPoint(l));

}

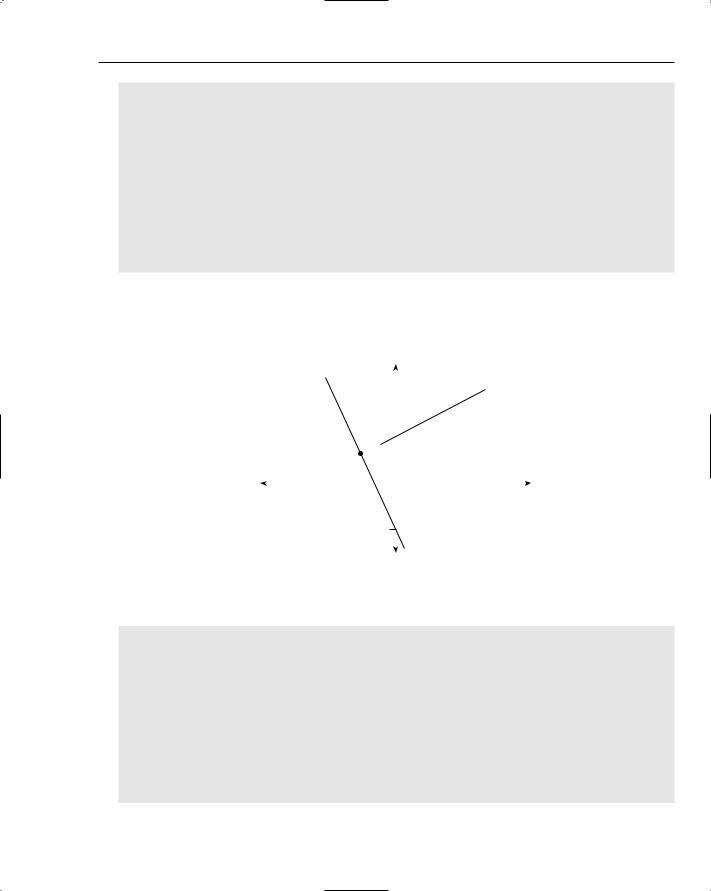
Finally, consider when the two lines are arranged such that they have a theoretical point of intersection, but the lines themselves are not long enough to include that point in one or other of the lines. Such lines are called disjoint lines. Figure 18-13 shows a pair of disjoint lines with their theoretical point of intersection marked:

Figure 18-13: A pair of disjoint lines.

Here is the code to ensure the correct behavior in this case:

public void testDisjointLinesDoNotIntersect() { Point p = new Point(0, 0);

Point q = new Point(0, 3); Point r = new Point(5, 0); Point s = new Point(-1, -3);

Line l = new Line(p, q);

Line m = new Line(r, s);

assertNull(l.intersectionPoint(m));

assertNull(m.intersectionPoint(l));

}

}

453