Beginning Algorithms (2006)

Chapter 17

}

++stringIndex;

}

return String.valueOf(result);

}

private static char map(char c) {

int index = Character.toUpperCase(c) - ‘A’;

return isValid(index) ? CHARACTER_MAP[index] : ‘0’;

}

private static boolean isValid(int index) {

return index >= 0 && index < CHARACTER_MAP.length;

}

}

How It Works

By defining the PhoneticEncoder interface, you will be able to develop other variations that can be used in your own applications without depending directly on the specific implementation presented here:

package com.wrox.algorithms.wmatch;

public interface PhoneticEncoder {

public String encode(CharSequence string);

}

The SoundexPhoneticEncoder class then implements the PhoneticEncoder interface to ensure pluggability with different encoding schemes if you so desire.

Notice that the constructor is marked as private, which prevents instantiation. Recall that earlier we mentioned we would only ever need a single instance of the class, so all access to the class must be via the publicly available constant INSTANCE.

Notice also the character array CHARACTER_MAP. This is crucial to the algorithm and provides a mapping between characters and coded digits. The map is assumed to start at A and continue on through the alphabet until Z. Obviously, this limits the implementation to working only with the English language, but as the algorithm only really works for English names, this isn’t much of a problem:

package com.wrox.algorithms.wmatch;

public final class SoundexPhoneticEncoder implements PhoneticEncoder { public static final SoundexPhoneticEncoder INSTANCE =

new SoundexPhoneticEncoder();

private static final char[] CHARACTER_MAP = “01230120022455012623010202”.toCharArray();

private SoundexPhoneticEncoder() {

}

...

}

424

String Matching

Before getting into the core of the algorithm, we’ll first cover two simple helper methods: map() and isValid(). Together, these methods take a character from the input string and translate it according to the Soundex rules. The character is first converted into an index that can be used for looking up values in the array CHARACTER_MAP. If the index falls within the bounds of the array, the character is translated; otherwise, a 0 is returned to indicate that it should be ignored — just as for vowels:

private static char map(char c) {

int index = Character.toUpperCase(c) - ‘A’;

return isValid(index) ? CHARACTER_MAP[index] : ‘0’;

}

private static boolean isValid(int index) {

return index >= 0 && index < CHARACTER_MAP.length;

}

Finally, you get to the actual Soundex encoding algorithm: encode(). This method starts by initializing a four-character array with all zeros. This is actually a shortcut method of padding the final encoded value — you already know the result must be four characters in length, so why not start off with all zeros? Next, the first character of the input string is used as the first character of the result — and converted to uppercase just in case — as per rule 1. The method then loops over each character of the input string. Each character is passed through map() and the return value is stored in the result buffer — unless it is 0 or the same as the last value stored, in which case it is ignored. This continues until either the result buffer is full — four characters have been stored — or there are no more input characters to process. The result buffer is then converted to a string and returned to the caller:

public String encode(CharSequence string) {

assert string != null : “string can’t be null”; assert string.length() > 0 : “string can’t be empty”;

char[] result = {‘0’, ‘0’, ‘0’, ‘0’};

result[0] = Character.toUpperCase(string.charAt(0));

int stringIndex = 1; int resultIndex = 1;

while (stringIndex < string.length() && resultIndex < result.length) { char c = map(string.charAt(stringIndex));

if (c != ‘0’ && c != result[resultIndex - 1]) { result[resultIndex] = c;

++resultIndex;

}

++stringIndex;

}

return String.valueOf(result);

}

425

Chapter 17

Understanding Levenshtein Word Distance

While phonetic coding such as Soundex is excellent for fuzzy-matching misspelled English names and even some minor spelling mistakes, it isn’t very good at detecting large typing errors. For example, the Soundex values for “mistakes” and “msitakes” are the same, but the values for “shop” and “sjop” are not, even though transposing a “j” for an “h” is a common mistake — both letters are next to each other on a standard QWERTY keyboard.

The Levenshtein word distance (also known as edit distance) algorithm compares words for similarity by calculating the smallest number of insertions, deletions, and substitutions required to transform one string into another. You can then choose some limit — say, 4 — below which the distance between two words is short enough to consider. Thus, the algorithm presented often forms the basis for a number of other techniques used in word processor spell-checking, DNA matching, and plagiarism detection.

The algorithm uses an effective yet rather brute-force approach that essentially looks at every possible way of transforming the source string to the target string to find the least number of changes.

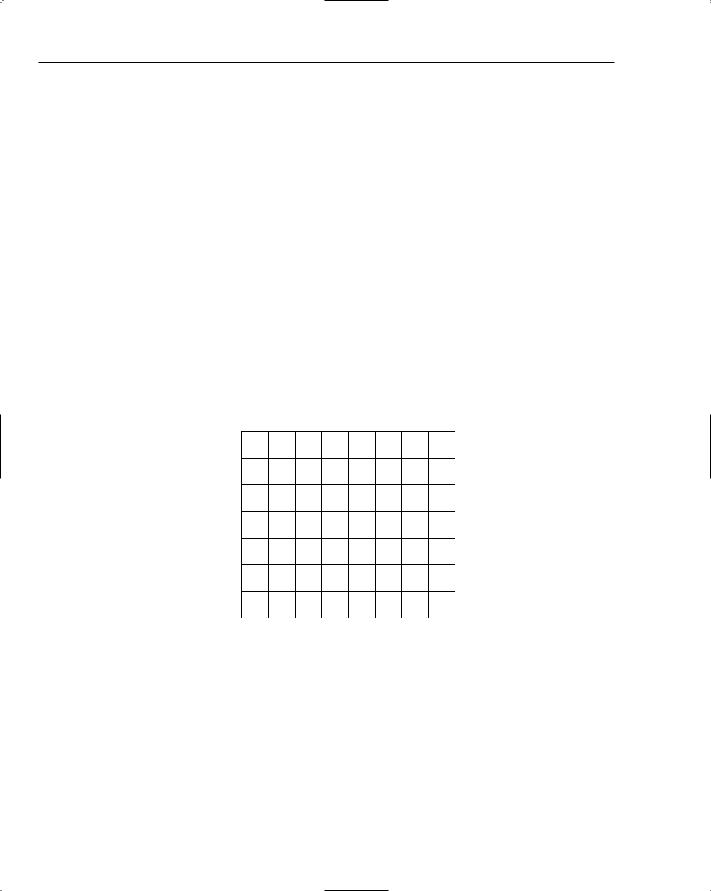
Three different operations can be performed. Each operation is assigned a cost, and the smallest distance is the set of changes with the smallest total cost. To calculate the Levenshtein distance, start by creating a grid with rows and columns corresponding to the letters in the source and target word. Figure 17-10 shows the grid for calculating the edit distance from “msteak” to “mistake”.

m i s t a k e

0 1 2 3 4 5 6 7

m 1

s2

t3

e 4

a 5

k 6

Figure 17-10: Initialized grid for comparing msteak with mistake.

Notice we’ve also included an extra row with the values 1–7 and an extra column with the values 1–6. The row corresponds to an empty source word and the values represent the cumulative cost of inserting each character. The column corresponds to an empty target word and the values represent the cumulative cost of deletion.

The next step is to calculate the values for each of the remaining cells in the grid. The value for each cell is calculated according to the following formula:

min(left diagonal + substitution cost, above + delete cost, left + insert cos)

For example, to calculate the value for the first cell (m, m), you apply the following formula:

426

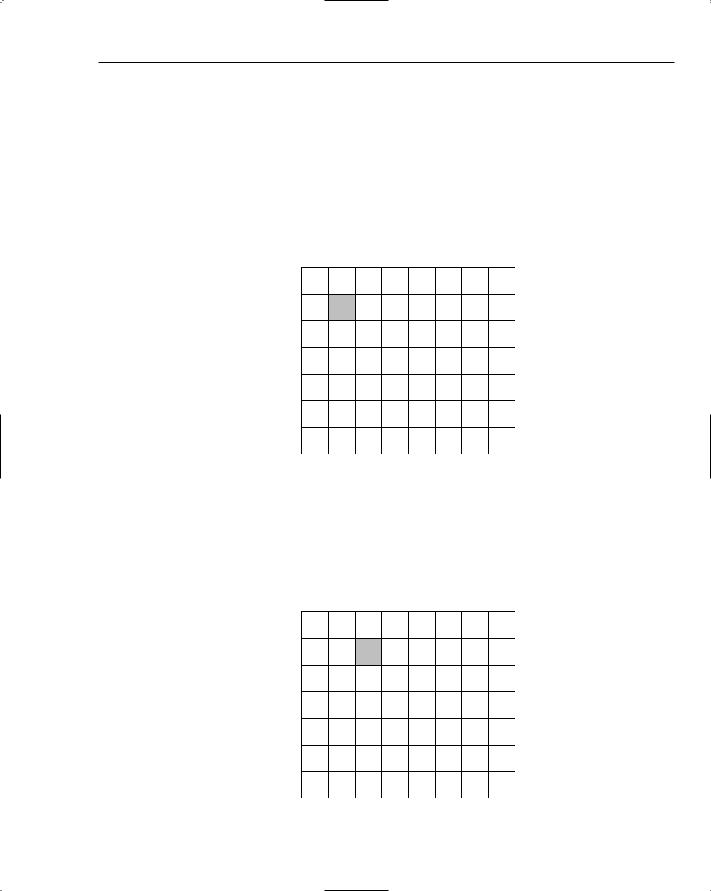
String Matching

min(0 + 0, 1 + 1, 1 + 1) = min(0, 2, 2) = 0

The cost for insertion and deletion is always one, but the cost for substitution is only one when the source and target characters don’t match.

You might want to vary the cost for some operations — specifically, insertion and deletion — as you may consider the substitution of one character for another to be less costly than inserting or deleting a character.

Calculating the value for the cell leads to the grid shown in Figure 17-11.

m i s t a k e

m 1 0

s2

t3

e 4

a 5

k 6

Figure 17-11: Calculating the value for the first cell (m, m).

For the next cell (m, i), it would be as follows:

min(1 + 1, 2 + 1, 0 + 1) = min(2, 3, 1) = 1

This would result in the grid shown in Figure 17-12.

m i s t a k e

m 1 0 1

s2

t3

e 4

a 5

k 6

Figure 17-12: Calculating the value for the next cell (m, i).

427

Chapter 17

This process continues until every cell has been assigned a value, as shown in Figure 17-13.

m i s t a k e

0 1 2 3 4 5 6 7

m 1 0 1 2 3 4 5 6

Figure 17-13: A completed grid. The last cell (k, e) has the minimum distance.

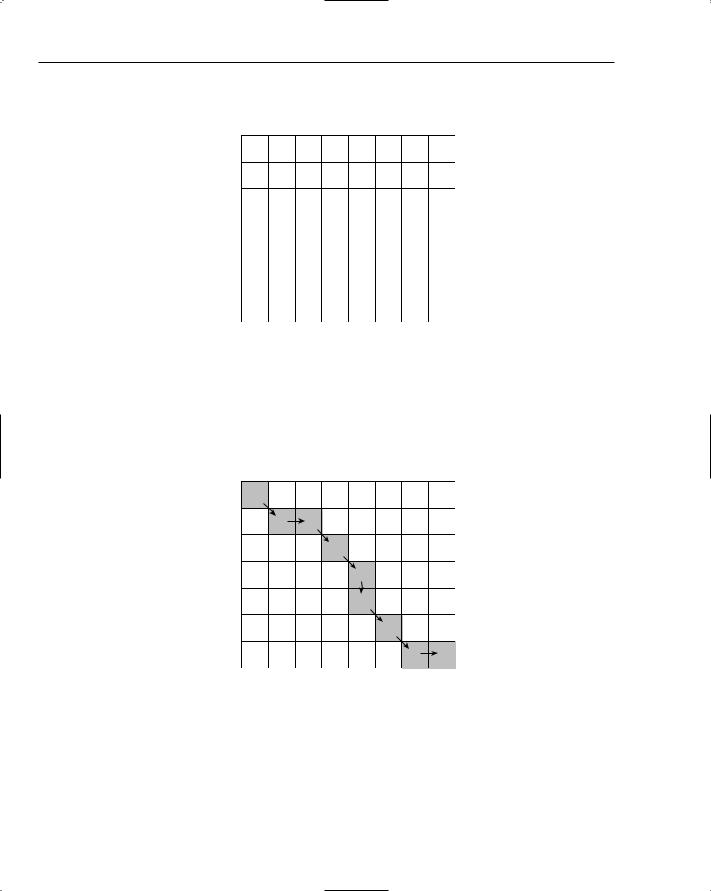
The value in the bottom-right cell of the grid shows that the minimum distance between “msteak” and “mistake” is 3. The grid actually provides a set of operations (or alignments) that you can apply to transform the source to the target. Figure 17-14 shows just one of the many paths that make up a set of transformations.

Figure 17-14: One of many possible paths through the grid showing the order of operations for transforming “msteak” into “mistake”.

You can interpret Figure 17-14 as follows”

428

String Matching

From this, you can deduce that a move diagonally down is a substitution; to the right an insertion; and straight down a deletion.

The algorithm as just defined performs in a time relative to O(MN), as each character from the source, M, is compared with each character in the target, N, to produce a fully populated grid. This means that the algorithm as it stands couldn’t really be used for producing a spell-checker containing any appreciable number of words, as the time to calculate all the distances would be prohibitive. Instead, word processors typically use a combination of techniques similar to those presented in this chapter.

In the following Try It Out, you build some tests that ensure that your implementation of the algorithm runs correctly.

Create the test class as follows:

package com.wrox.algorithms.wmatch;

import junit.framework.TestCase;

public class LevenshteinWordDistanceCalculatorTest extends TestCase { private LevenshteinWordDistanceCalculator _calculator;

protected void setUp() throws Exception { super.setUp();

_calculator = LevenshteinWordDistanceCalculator.DEFAULT;

}

public void testEmptyToEmpty() { assertDistance(0, “”, “”);

}

public void testEmptyToNonEmpty() { String target = “any”;

assertDistance(target.length(), “”, target);

}

public void testSamePrefix() { assertDistance(3, “unzip”, “undo”);

}

public void testSameSuffix() { assertDistance(4, “eating”, “running”);

}

public void testArbitrary() {

429

Chapter 17

assertDistance(3, “msteak”, “mistake”); assertDistance(3, “necassery”, “neccessary”); assertDistance(5, “donkey”, “mule”);

}

private void assertDistance(int distance, String source, String target) { assertEquals(distance, _calculator.calculate(source, target)); assertEquals(distance, _calculator.calculate(target, source));

}

}

How It Works

The LevenshteinWordDistanceCalculatorTest class holds an instance of a

LevenshteinWordDistanceCalculator to be used by the tests. This is then initialized with the default instance described earlier:

package com.wrox.algorithms.wmatch;

import junit.framework.TestCase;

public class LevenshteinWordDistanceCalculatorTest extends TestCase { private LevenshteinWordDistanceCalculator _calculator;

protected void setUp() throws Exception { super.setUp();

_calculator = LevenshteinWordDistanceCalculator.DEFAULT;

}

...

}

The method assertDistance() is used in all of the tests to ensure that the calculated distance is as expected. It takes a source string and a target string and runs them through the calculator, comparing the result with the expected value. The thing to note about this method — and the reason you have created it — is that it runs the calculation twice, swapping the source and target the second time around. This ensures that no matter which way the strings are presented to the calculator, the same distance value is always produced:

private void assertDistance(int distance, String source, String target) { assertEquals(distance, _calculator.calculate(source, target)); assertEquals(distance, _calculator.calculate(target, source));

}

The method testEmptyToEmpty() ensures that the distance between two empty strings is zero — even though they are empty, both strings are effectively the same:

public void testEmptyToEmpty() { assertDistance(0, “”, “”);

}

430

String Matching

The method testEmptyToNonEmpty() compares an empty string with an arbitrary non-empty string: The distance should be the length of the non-empty string itself:

public void testEmptyToNonEmpty() { String target = “any”;

assertDistance(target.length(), “”, target);

}

Next, testSamePrefix() tests strings sharing a common prefix: The distance should be the length of the longer string minus the prefix:

public void testSamePrefix() { assertDistance(3, “unzip”, “undo”);

}

Conversely, testSamePrefix() test strings sharing a common suffix: This time, the distance should be the length of the longer string minus the suffix:

public void testSameSuffix() { assertDistance(4, “eating”, “running”);

}

Finally, you tested various combinations with known distances:

public void testArbitrary() { assertDistance(3, “msteak”, “mistake”);

assertDistance(3, “necassery”, “neccessary”); assertDistance(5, “donkey”, “mule”);

}

Now that you have some tests to back you up, in the following Try It Out section, you create the actual distance calculator.

Create the distance calculator as follows:

package com.wrox.algorithms.wmatch;

public class LevenshteinWordDistanceCalculator {

public static final LevenshteinWordDistanceCalculator DEFAULT = new LevenshteinWordDistanceCalculator(1, 1, 1);

private final int _costOfSubstitution; private final int _costOfDeletion; private final int _costOfInsertion;

public LevenshteinWordDistanceCalculator(int costOfSubstitution, int costOfDeletion, int costOfInsertion) {

assert costOfSubstitution >= 0 : “costOfSubstitution can’t be < 0”; assert costOfDeletion >= 0 : “costOfDeletion can’t be < 0”;

431

Chapter 17

assert costOfInsertion >= 0 : “costOfInsertion can’t be < 0”;

_costOfSubstitution = costOfSubstitution; _costOfDeletion = costOfDeletion; _costOfInsertion = costOfInsertion;

}

public int calculate(CharSequence source, CharSequence target) { assert source != null : “source can’t be null”;

assert target != null : “target can’t be null”;

int sourceLength = source.length(); int targetLength = target.length();

int[][] grid = new int[sourceLength + 1][targetLength + 1];

grid[0][0] = 0;

for (int row = 1; row <= sourceLength; ++row) { grid[row][0] = row;

}

for (int col = 1; col <= targetLength; ++col) { grid[0][col] = col;

}

for (int row = 1; row <= sourceLength; ++row) { for (int col = 1; col <= targetLength; ++col) {

grid[row][col] = minCost(source, target, grid, row, col);

}

}

return grid[sourceLength][targetLength];

}

private int minCost(CharSequence source, CharSequence target, int[][] grid, int row, int col) {

return min(

substitutionCost(source, target, grid, row, col), deleteCost(grid, row, col),

insertCost(grid, row, col)

);

}

private int substitutionCost(CharSequence source, CharSequence target, int[][] grid, int row, int col) {

int cost = 0;

if (source.charAt(row - 1) != target.charAt(col – 1)) { cost = _costOfSubstitution;

}

return grid[row - 1][col - 1] + cost;

}

private int deleteCost(int[][] grid, int row, int col) { return grid[row - 1][col] + _costOfDeletion;

432

String Matching

}

private int insertCost(int[][] grid, int row, int col) { return grid[row][col - 1] + _costOfInsertion;

}

private static int min(int a, int b, int c) { return Math.min(a, Math.min(b, c));

}

}

How It Works

The LevenshteinWordDistanceCalculator class has three instance variables for storing the unit cost associated with each of the three operations: substitution, deletion, and insertion. The class also defines a DEFAULT whereby all three operations have a unit cost of one, as was the case in the discussion earlier. There is also a public constructor that enables you to play with different weightings:

package com.wrox.algorithms.wmatch;

public class LevenshteinWordDistanceCalculator {

public static final LevenshteinWordDistanceCalculator DEFAULT = new LevenshteinWordDistanceCalculator(1, 1, 1);

private final int _costOfSubstitution; private final int _costOfDeletion; private final int _costOfInsertion;

public LevenshteinWordDistanceCalculator(int costOfSubstitution, int costOfDeletion, int costOfInsertion) {

assert costOfSubstitution >= 0 : “costOfSubstitution can’t be < 0”; assert costOfDeletion >= 0 : “costOfDeletion can’t be < 0”;

assert costOfInsertion >= 0 : “costOfInsertion can’t be < 0”;

_costOfSubstitution = costOfSubstitution; _costOfDeletion = costOfDeletion; _costOfInsertion = costOfInsertion;

}

...

}

Before getting into the core of the algorithm, let’s start by examining some of the intermediate calculations. The first such calculation is substitutionCost(). As the name implies, this method calculates the cost of substituting one character for another. Recall that the substitution cost is 0 if the two letters are the same, or 1 + the value in the diagonally left cell.

The method starts off by assuming the characters will match, therefore initializing the cost to 0. You then compare the two characters, and if they differ, the cost is updated accordingly. Finally, you add in the cumulative value stored in the diagonally left cell of the grid before returning the value to the caller:

private int substitutionCost(CharSequence source, CharSequence target, int[][] grid, int row, int col) {

int cost = 0;

433