Beginning Algorithms (2006)

Chapter 16

As demonstrated a little later, this capability to skip entire sections of text leads to some pretty amazing performance improvements over the brute-force search. In fact, although highly unlikely, if the text is such that no character from the pattern ever occurs, then the entire length of the pattern can be skipped each time, leading to a best-case running time of O(N/M), where N is the length of the text to search and M is the length of the pattern.

Following along the same lines as the previous implementation, you can now create both a test class and a searcher named after the algorithm.

Creating the Tests

Again, you can make use of the tests defined in our abstract test case. This time, however, you will define an additional test specific to the Boyer-Moore implementation.

Create a test class as shown here:

package com.wrox.algorithms.ssearch;

public class BoyerMooreStringSearcherTest extends AbstractStringSearcherTestCase {

protected StringSearcher createSearcher(CharSequence pattern) { return new BoyerMooreStringSearcher(pattern);

}

public void testShiftsDontErroneouslyIgnoreMatches() { String text = “aababaa”;

String pattern = “baba”;

StringSearcher searcher = createSearcher(pattern);

StringMatch match = searcher.search(text, 0); assertNotNull(match);

assertEquals(text, match.getText()); assertEquals(pattern, match.getPattern()); assertEquals(2, match.getIndex());

assertNull(searcher.search(text, match.getIndex() + 1));

}

}

How It Works

Because the Boyer-Moore algorithm can shift more than one position at a time, you need to ensure that it shifts the correct number of places. The pattern in this case contains two occurrences of each character. If there was a bug in your calculation of the last occurrence, you might shift too many or too few places.

Implementing the Algorithm

There are several steps involved in implementing the Boyer-Moore algorithm. You must create a string searcher code, compute the last occurrence table, and finally perform the search.

404

String Searching

Start with the basic class definition:

package com.wrox.algorithms.ssearch;

public class BoyerMooreStringSearcher implements StringSearcher { private final CharSequence _pattern;

private final short[] _lastOccurrence;

public BoyerMooreStringSearcher(CharSequence pattern) { assert pattern != null : “pattern can’t be null”;

assert pattern.length() > 0 : “pattern can’t be empty”;

_pattern = pattern;

_lastOccurrence = computeLastOccurrence(pattern);

}

...

}

How It Works

So far, this class looks very similar to the brute-force code except for the presence of the array _lastOccurrence and the call to computeLastOccurrences to initialize it. If you recall, the BoyerMoore algorithm needs to know the position of the last occurrence of each character in the pattern. You could calculate this repeatedly by scanning the pattern as needed, but this would certainly add significant overhead, or you could calculate the values once, store them, and look them up as needed.

The construction of the lookup table does incur a once-off overhead proportional to the length of the pattern and size of the character set used. For small character sets such as ASCII, the overhead is minimal. However, larger character sets, such as those required to represent Asian and Middle-Eastern languages, may require more sophisticated techniques, which are beyond the scope of this book.

The method computeLastOccurrences() takes the pattern and returns an array containing the position (0, 1, 2, . . .) of the last occurrence of each character. This is then stored in the _lastOccurrence variable for later use:

private static short[] computeLastOccurrence(CharSequence pattern) { short[] lastOccurrence = new short[CHARSET_SIZE];

for (int i = 0; i < lastOccurrence.length; ++i) { lastOccurrence[i] = -1;

}

for (int i = 0; i < pattern.length(); ++i) { lastOccurrence[pattern.charAt(i)] = (short) i;

}

return lastOccurrence;

}

405

Chapter 16

How It Works

Here you have assumed the use of the ASCII character set, so you first construct an array containing 256 elements — one for each character — and initialize each with a value of –1 to indicate that, by default, it doesn’t exist within the pattern.

You then iterate from left to right over each character in the pattern, using its character code as an index to the element at which to record the position. Processing the pattern in this way ensures that the position of each character will be overwritten by that of any duplicate that follows, thereby guaranteeing that the array always holds the position of the last (rightmost) occurrence.

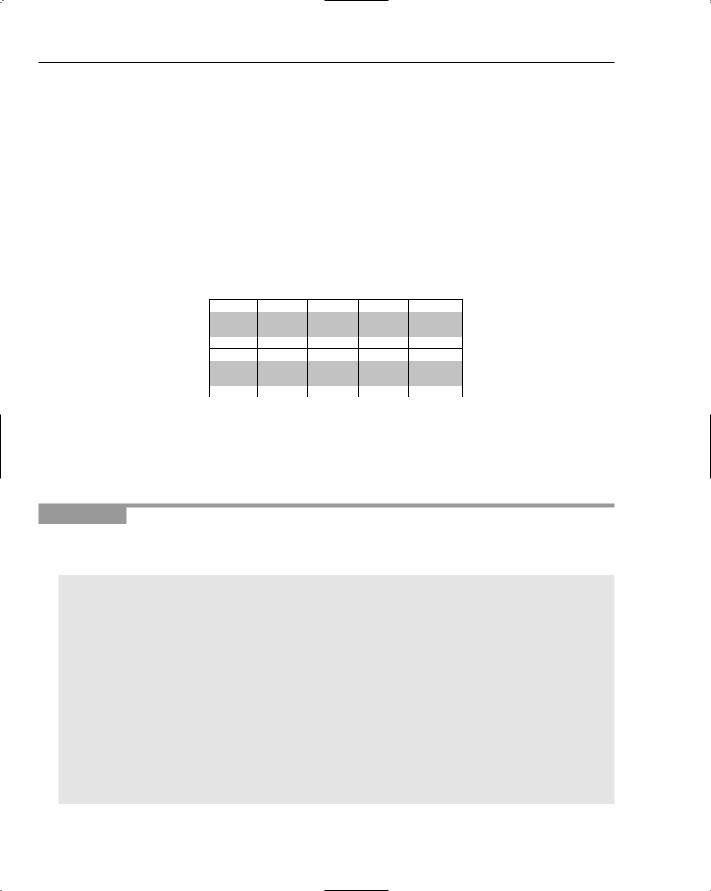
Imagine you have a very simplistic character set containing only five characters: A , B, C, D, and E. From this, you can define a pattern, DECADE, and construct a corresponding last occurrence table, as shown in Figure 16-1.

Figure 16-1: A last occurrence table.

The pattern contains one A at position 3 and one C at position 2, but no B, which has consequently been set to –1. Both D and E, however, occur twice and have been assigned the rightmost position — 4 and 5, respectively.

As with the brute-force approach, you could simply increment the current position within the text by one each time, but the Boyer-Moore algorithm calls for something more sophisticated:

public StringMatch search(CharSequence text, int from) { assert text != null : “text can’t be null”;

assert from >= 0 : “from can’t be < 0”;

int s = from;

while (s <= text.length() - _pattern.length()) { int i = _pattern.length() - 1;

char c = 0; while (i >= 0

&& _pattern.charAt(i) == (c = text.charAt(s + i))) { --i;

}

if (i < 0) {

return new StringMatch(_pattern, text, s);

406

String Searching

}

s += Math.max(i - _lastOccurrence[c], 1);

}

return null;

}

How It Works

The search() method itself is structurally very similar to the brute-force version, with two notable differences:

The pattern is compared backwards, i.e., from right-to-left.

Determining the shift involves an array lookup and a calculation.

Here is the code that performs the shift calculation:

s += Math.max(i - _lastOccurrence[c], 1);

Performing the calculation is quite straightforward: You take the mismatched character from the text and use it to look up its last known position (0, 1, 2, . . .) within the pattern. This is then subtracted from the current position within the pattern. As an example, imagine you were to compare the pattern abcd with the text bdaaedccda:

bdaaedccda abcd------

The first mismatch occurs immediately when d (position 3 within the pattern) is compared with a. The last occurrence of a within the pattern is at position 0, so subtracting one from the other results in a shift of 3 - 0 = 3. Moving three place to the right, you next compare abcd with aaed:

bdaaedccda --abcd----

Although the two ds match, the previous two characters (position 2 within the pattern) do not, and as there is no e within the pattern, the table lookup yields a value of –1; when used in our calculation, this gives us a shift of 2 - –1 = 3. Moving right another three places leads to a comparison of abcd with dccd:

bdaaedccda

-----abcd-

Here you find a mismatch between the b (position 1 within the pattern) and the c from the text. The last place a c occurs within the pattern is at position 2, giving us a shift of 1 – 2 = –1; you certainly don’t want to be sliding backwards.

Recall, however, that the last part of our three-part heuristic deals with negative shifts. In such cases, the procedure is to resort to the naive approach of shifting right by one. Thus, the call to Math.max(..., 1) ensures that no matter what value is calculated, you always end up with an increment of at least one.

407

Chapter 16

A String Match Iterator

If you take a look at the test cases, you may notice that anytime you wanted to iterate through a number of matches, you needed to remember your current location. This approach, though good enough for our needs so far, would ultimately force a duplication of coding effort: Every time you want to perform a search, you need to remember not only the text you are searching through, but also the current position. What you really need is another class to sit on top of a searcher and encapsulate this behavior.

Chapter 2 introduced the Iterator, and throughout this book you have made good use of it. Create the following class, which demonstrates yet again the power and flexibility of the iterator and of our string searcher design by encapsulating the behavior and state required to perform multiple, successive searches:

package com.wrox.algorithms.ssearch;

import com.wrox.algorithms.iteration.Iterator;

import com.wrox.algorithms.iteration.IteratorOutOfBoundsException;

public class StringMatchIterator implements Iterator { private final StringSearcher _searcher;

private final CharSequence _text; private StringMatch _current;

public StringMatchIterator(StringSearcher searcher, CharSequence text) { assert searcher != null : “searcher can’t be null”;

assert text != null : “text can’t be null”;

_searcher = searcher; _text = text;

}

public void last() {

throw new UnsupportedOperationException();

}

public void previous() {

throw new UnsupportedOperationException();

}

public boolean isDone() { return _current == null;

}

public void first() {

_current = _searcher.search(_text, 0);

}

public void next() { if (!isDone()) {

_current = _searcher.search(_text, _current.getIndex() + 1);

408

String Searching

}

}

public Object current() throws IteratorOutOfBoundsException { if (isDone()) {

throw new IteratorOutOfBoundsException();

}

return _current;

}

}

How It Works

The StringMatchIterator class holds the string searcher to use; the text to search; and, of course, the current match (if any). It is therefore assumed that you will already have created a string searcher before constructing the string match iterator.

Both last() and previous() throw UnsupportedOperationException. This is because the

StringSearcher interface provides only for searching forwards through the text.

Implementing isDone() is simple, as the string searcher always returns null when no more matches are found.

Finding the first match is a matter of calling the string searcher with an initial character position of 0 — the start of the string.

Finding the next and subsequent matches is where you gain most from having the iterator. Because you always hold on to the result of any previous match, you can easily calculate the character position that is one to the right of it in order to continue the search.

Finally, you make the current match accessible via the current() method, again making sure to throw

IteratorOutOfBoundsException if there isn’t one.

Comparing the Performance

Now that you have your working string searching algorithms, you probably want to see how they compare with each other. We are pretty confident that the Boyer-Moore algorithm will outperform the bruteforce algorithm, but how do we prove it? Usually you would come up with a suite of tests for calculating the best, worst, and average case times. Instead, we thought a more practical example would be of interest: searching a file.

This section develops a simple application that exercises our string searchers by looking for patterns within a file. In the process, you’ll demonstrate a simple technique to enable measuring the relative performance of each search implementation.

Measuring Performance

There are many ways to measure the performance of algorithms. The most obvious, of course, is to record elapsed running time. Unfortunately, running times are often susceptible to unpredictable interference

409

Chapter 16

from operating system functions such as virtual memory swapping, task switching, network interrupts, and so on. You really need to find a more predictable measure.

Most of the performance-related discussion so far has centered around the number of comparisons made. In fact, the entire basis for deviating from the brute-force algorithm is to reduce not only the number of string comparisons, but also the number of character comparisons — by reducing the number of character comparisons, you reduce the amount of work; by reducing the amount of work, you should in theory reduce the overall running time. Therefore, if you could count the number of comparisons performed, you should be able to measure the performance of each algorithm.

Reviewing the code, it becomes apparent that in both implementations, for each comparison made, there are two character lookups: one to obtain a character from the text, and another from the pattern. From this, you can infer a direct relationship between character lookups and comparisons: If you can count the number of lookups, you can measure the relative performance.

You may recall that instead of using Strings for the text and pattern, you used the interface CharSequence. Another reason to use the interface is because it becomes trivial to create a wrapper (see Decorator [Gamma, 1995]) that can intercept and count every call to charAt() — yet another good reason to use interfaces over concrete classes.

Here is a class that does exactly what you need — namely, count character lookups:

package com.wrox.algorithms.ssearch;

public class CallCountingCharSequence implements CharSequence { private final CharSequence _charSequence;

private int _callCount;

public CallCountingCharSequence(CharSequence charSequence) { assert charSequence != null : “charSequence can’t be null”; _charSequence = charSequence;

}

public int getCallCount() { return _count;

}

public char charAt(int index) { ++_count;

return _charSequence.charAt(index);

}

public int length() {

return _charSequence.length();

}

public CharSequence subSequence(int start, int end) { return _charSequence.subSequence(start, end);

}

}

410

String Searching

How It Works

Besides implementing CharSequence, the class CallCountingCharSequence wraps and eventually delegates all method calls to another underlying CharSequence. Notice how each call to charAt() increments a counter. This counter is then made accessible via the getCallCount() method. In this way, it is very easy to determine how many character comparisons have been made.

Now that you have a way to count character lookups, you need a way to search through files:

import com.wrox.algorithms.iteration.Iterator;

import java.io.FileInputStream; import java.io.IOException; import java.nio.ByteBuffer; import java.nio.CharBuffer;

import java.nio.channels.FileChannel; import java.nio.charset.Charset;

public final class ComparativeStringSearcher { private static final int NUMBER_OF_ARGS = 2;

private static final String CHARSET_NAME = “8859_1”;

private final String _filename; private final String _pattern;

public ComparativeStringSearcher(String filename, String pattern) { assert filename != null : “filename can’t be null”;

assert pattern != null : “pattern can’t be null”;

_filename = filename; _pattern = pattern;

}

public void run() throws IOException {

FileChannel fc = new FileInputStream(_filename).getChannel(); try {

ByteBuffer bbuf =

fc.map(FileChannel.MapMode.READ_ONLY, 0, (int) fc.size());

CharBuffer file =

Charset.forName(CHARSET_NAME).newDecoder().decode(bbuf);

System.out.println(“Searching ‘“ + _filename + “‘ (“

+ file.length() + “) for ‘“ + _pattern + “‘...”);

search(new BruteForceStringSearcher(_pattern), file); search(new BoyerMooreStringSearcher(_pattern), file);

} finally { fc.close();

}

}

private void search(StringSearcher searcher, CharSequence file) {

411

Chapter 16

CallCountingCharSequence text = new CallCountingCharSequence(file);

Iterator i = new StringMatchIterator(searcher, text);

int occurrence = 0;

long startTime = System.currentTimeMillis();

for (i.first(); !i.isDone(); i.next()) { ++occurrence;

}

long elapsedTime = System.currentTimeMillis() - startTime;

System.out.println(searcher.getClass().getName()

+“: occurrences: “ + occurrence

+“, comparisons: “ + text.getCallCount()

+“, time: “ + elapsedTime);

}

public static void main(String[] args) throws IOException { assert args != null : “args can’t be null”;

if (args.length < NUMBER_OF_ARGS) { System.err.println(

“Usage: ComparativeStringSearcher <file> <pattern>”); System.exit(-1);

}

ComparativeStringSearcher searcher =

new ComparativeStringSearcher(args[0], args[1]);

searcher.run();

}

}

How It Works

Most modern operating systems enable you to open memory-mapped files — instead of reading them as a stream, you can address them as if they were a contiguous array of bytes in memory. You can take advantage of memory-mapped files in your Java programs by using, among others, the java.nio.CharBuffer class. What does this have to do with what we’re talking about? Well, the truly great thing about CharBuffer is that it implements CharSequence, which, if you haven’t already guessed, means you can use a file as input to the searching algorithms, which is exactly what this class does.

The run() method opens the file specified in the constructor and creates a CharBuffer that enables you to read from the file using memory-mapped I/O. This is then passed along with a string searcher to the search() method, twice: once for each of the two string searcher implementations you created earlier.

The search() method first wraps the file with a CallCountingCharSequence — a CharBuffer is a

CharSequence — to count the number of character lookups, and then uses a StringMatchIterator to find all occurrences of the pattern.

412

String Searching

Finally, the main() method is called when this program is run. It simply ensures that the correct number of arguments have been passed — one for the file in which to search and another for the pattern — before calling search(), where all the real work will be performed.

You may also have noticed the strange “8859_1”. This is a character set name and is necessary when using CharBuffers; otherwise, there would be no way of knowing how to decode the text in the file. The character set “8859_1” corresponds to ISO Latin-1, used for any Western European languages, including English. (See www.unicode.org for more information on character sets and character encoding.)

Now the big questions are: How efficient are the two algorithms? Which one is faster? More important, by how much?

How They Compare

To give you a good idea of how each performs, we thought we’d give them a good workout by searching through some large text files looking for various patterns. For this, we used Leo Tolstoy’s War and Peace — just a little over 3MB in size — available in plain-text format from the Gutenberg Projects website at www.gutenberg.org. Table 16-1 shows some of the results.

Table 16-1: Pattern Searching War and Peace

*The figures for Boyer-Moore include one extra lookup for each character due to the building of the last occurrence table.

As you can see, the Boyer-Moore algorithm performs consistently better than the naive algorithm — in almost all cases, more than twice as fast; and in most cases, more than four times faster! In fact, if you look carefully, you will notice that the longer the pattern, the greater the improvement. This is because the Boyer-Moore algorithm is often able to skip over large chunks of text — the longer the pattern, the more characters to skip, and consequently the better the performance.

Summar y

This chapter covered a few commonly used and well understood string searching algorithms — bruteforce and Boyer-Moore — and an iterator that sits on top of the common string searcher interface that removes the coding burden of making multiple, successive searches. Highlights of this chapter include the following main points:

413