
Beginning Algorithms (2006)
.pdf

15
B-Trees
So far, everything we’ve covered has been designed to work solely with in-memory data. From lists (Chapter 3) to hash tables (Chapter 11) and binary search trees (Chapter 10), all of the data structures and associated algorithms have assumed that the entire data set is held only in main memory, but what if the data exists on disk — as is the case with most databases? What if you wanted to search through a database for one record out of millions? In this chapter, you’ll learn how to handle data that isn’t stored in memory.
This chapter discusses the following topics:
Why the data structures you’ve learned so far are inadequate for dealing with data stored on disk
How B-Trees solve the problems associated with other data structures
How to implement a simple B-Tree-based map implementation
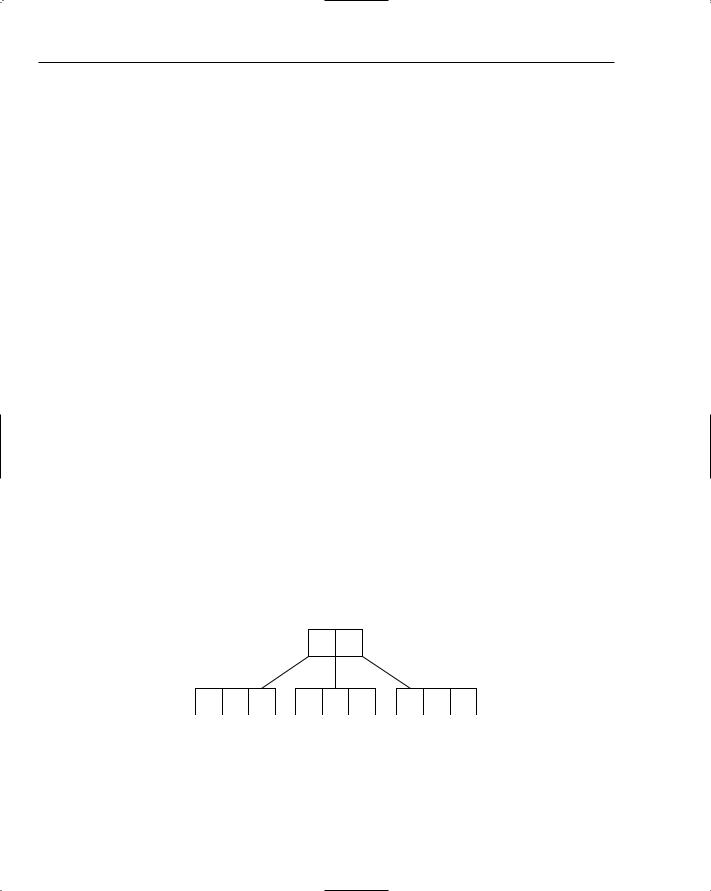
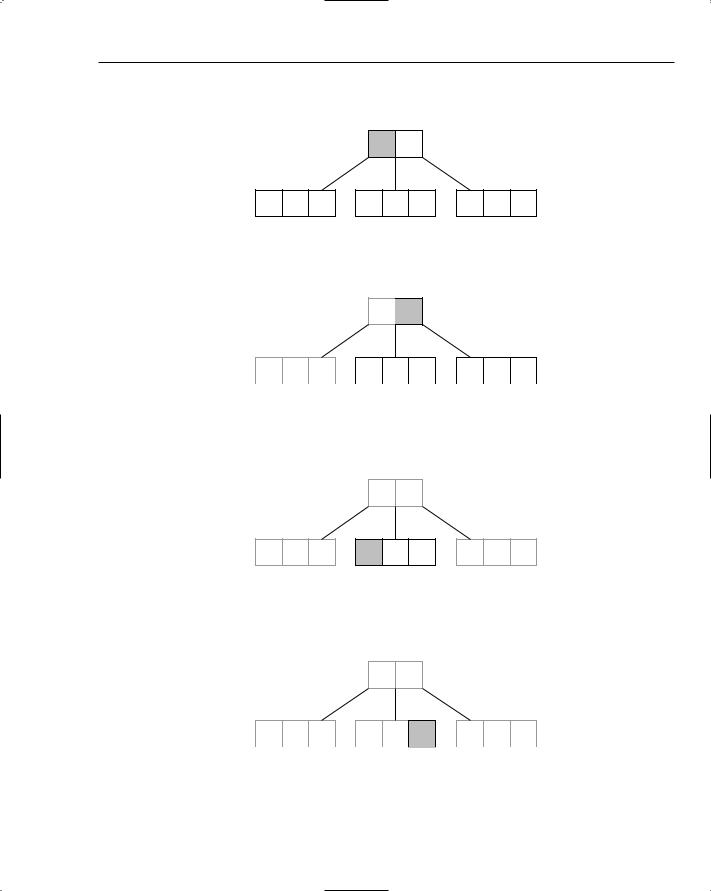
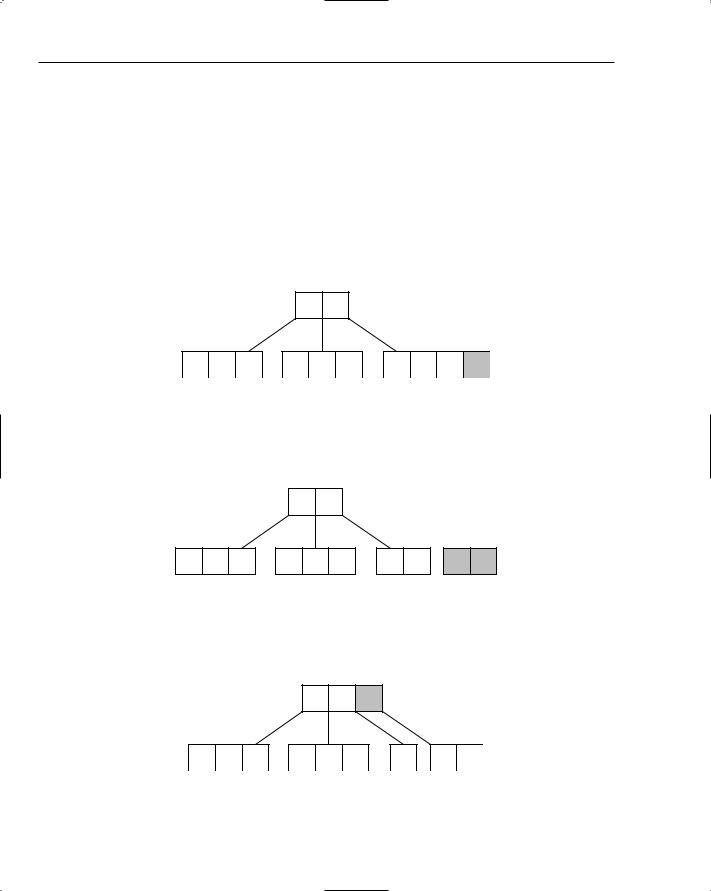
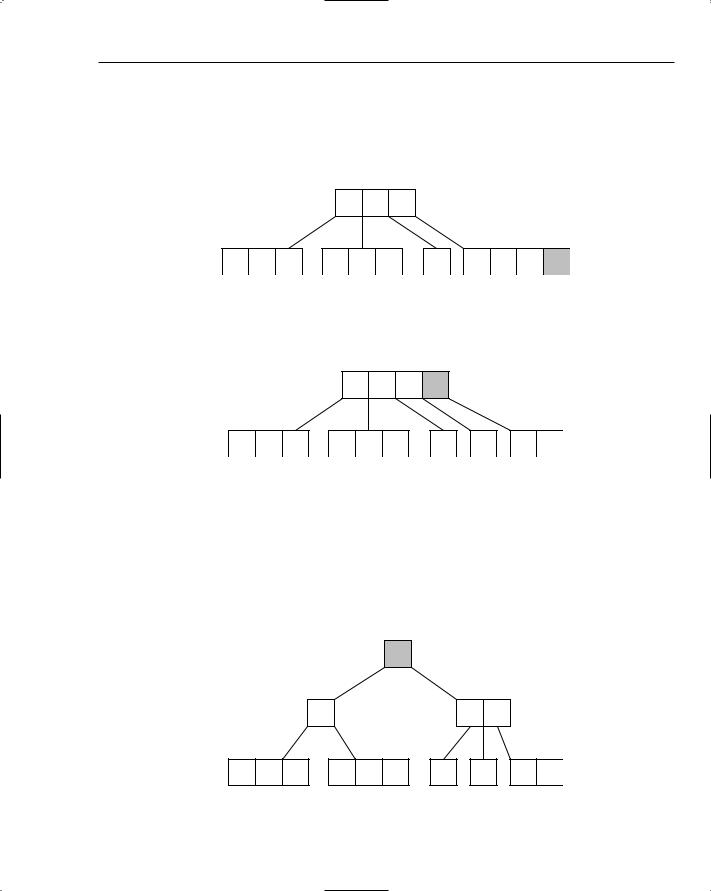
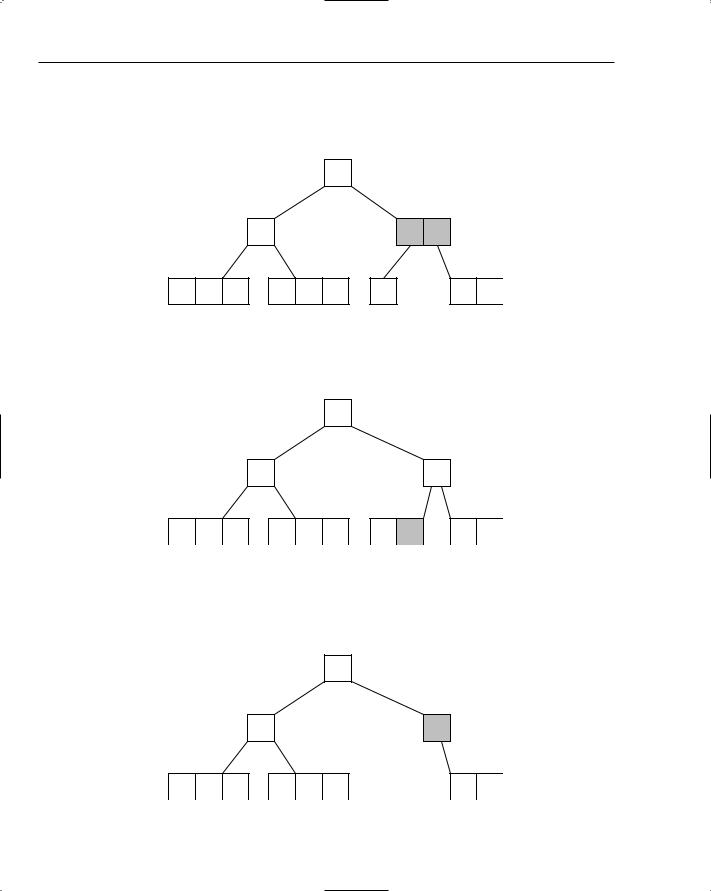
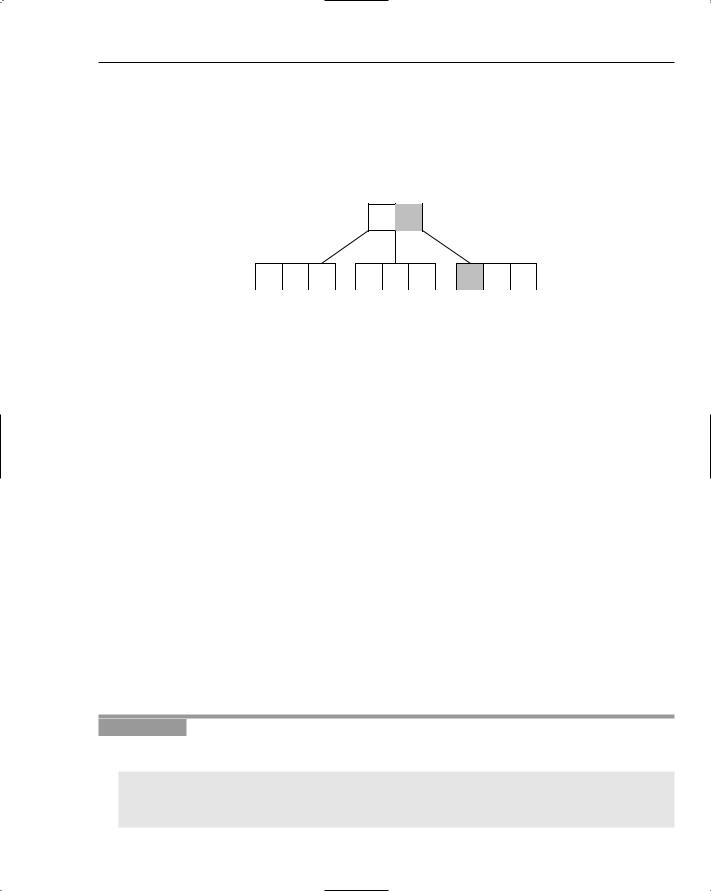
Understanding B-Trees
You’ve already seen how you can use binary search trees to build indexes as maps. It’s not too much of a stretch to imagine reading and writing the binary tree to and from disk. The problem with this approach, however, is that when the number of records grows, so too does the size of the tree. Imagine a database table holding a million records and an index with keys of length ten. If each key in the index maps to a record in the table (stored as integers of length four), and each node in the tree references its parent and child nodes (again each of length four), this would mean reading and writing 1,000,000 × (10 + 4 + 4 + 4 + 4) = 1,000,000 × 26 = 26,000,000 or approximately 26 megabytes (MB) each time a change was made!
That’s a lot of disk I/O and as you are probably aware, disk I/O is very expensive in terms of time. Compared to main memory, disk I/O is thousands, if not millions, of times slower. Even if you can achieve a data rate of 10MB/second, that’s still a whopping 2.6 seconds to ensure that any updates to the index are saved to disk. For most real-world applications involving tens if not hundreds of concurrent users, 2.6 seconds is going to be unacceptable. One would hope that you could do a little better than that.



 H
H