
Beginning Algorithms (2006)
.pdf
Chapter 5
Summar y
Although conceptually very simple, stacks underpin the operation of most computers. In this chapter you’ve learned the following:
Most CPUs, and therefore most programming languages, including Java, are stack-based.
Stacks always add and remove from the top — thus, they are often referred to as FIFO queues.
Stacks can easily be implemented on top of lists without constraining the implementation to one particular type of list.
There are many possible uses for stacks. This chapter demonstrated how easy it is to augment another data structure — in this case, a list — with an undo feature.
Now that you have seen some simple algorithms for string searching, and are familiar with managing your data using basic data structures such as lists, queues, and stacks, it is time to move on to solving more complex problems.
114

6
Basic Sor ting
Now that you understand some of the fundamental data structures used in today’s software applications, you can use those data structures to organize the large amounts of data that your applications need to process. Sorting data into a logical order is a critical prerequisite for many of the algorithms in the chapters to come, and it is such a potential performance bottleneck that an enormous amount of research has been done over many decades to determine the most efficient way to sort various types of data. This chapter introduces three sorting algorithms that are easy to implement and are best suited to smaller sets of data, as their performance is O(N2). Chapter 7 covers more complex sorting algorithms with better performance characteristics for very large data sets.
This chapter discusses the following:
The importance of sorting
The role of comparators
How the bubble sort algorithm works
How the selection sort algorithm works
How the insertion sort algorithm works
The meaning of stability
The pros and cons of the basic sorting algorithms
The Impor tance of Sor ting
You already know from the real world how important sorting is when working with searching algorithms. To look up a word in a dictionary, you use an algorithm: You open the dictionary at a point roughly equivalent to the word’s position in the sorted list of all the words in the dictionary. You then do a few quick narrowing searches until you find the page it’s on, and then finally scan the page for the word. Now imagine the words in the dictionary were not sorted. You’d probably decide to give up because the time to search the unsorted data would be prohibitive, and you’d be right!

Chapter 6
Without sorting, searching is impractical for very large sets of data. You could apply the same principle to many other types of data in the real world, such as the names in a phone book or the books on the shelves of a library. The problem with these examples is that you have never (I hope) had to deal with any of these types of data before they were sorted for you, so you’ve never had to create an efficient algorithm for sorting them. In the computer world, however, it is not uncommon to encounter sets of data just as large as these that arrive at your program unsorted, or in an order other than the one you need. A good grasp of the established algorithms helps you tackle this type of problem.
Sor ting Fundamentals
Sorting data into some kind of meaningful order requires a data structure that is capable of maintaining the order of its contents. As you learned in Chapter 4, this is the distinguishing feature of a list, so we will be using lists as the data structure on which the sorting algorithms operate.
After the objects to be sorted are contained in a list, all of the sorting algorithms are built upon two fundamental operations:
Comparing items to determine whether they are out of order
Moving items into sorted position
The advantages and disadvantages of each sorting algorithm are based on how many times these fundamental operations need to be performed and how expensive these operations are in performance terms. The task of comparing objects to determine whether they are sorted is a larger topic than you might at first imagine, so we will deal with it in the following section on comparators. The list data structure supports several methods for moving the objects — namely, get(), set(), insert(), and delete(). These operations are covered in detail in Chapter 3.
Understanding Comparators
In Java, as in many other languages, when you wish to compare two integers, you can do something like the following:
int x, y;
...
if (x < y) {
...
}
This works fine for primitive types, but things get more difficult when dealing with more complex objects. For example, when you look at a list of files on your computer, you might typically look at them sorted by their filename. Sometimes, however, you might want to look at them in the order they were created, or the order in which they were modified, or even by the type of file they happen to be.
It is important to support different orderings without having to write a whole new algorithm. This is where comparators come in. A comparator is responsible for imposing a specific ordering on objects, so
116

Basic Sorting
when you’re trying to sort files, you might have one comparator for filenames, one for file types, and yet another for modification times. All these comparators would enable a single sorting algorithm to sort a list of file objects in different ways.
This is an example of an important design principle known as separation of concerns. In this case, you separate the concern of how to compare two individual objects (the comparator) from the concern of how to efficiently sort a large list of objects (the algorithm). This enables you to extend the usefulness of an algorithm by plugging in comparators that you had not imagined when creating it, and enables you to reuse a given comparator across multiple algorithm implementations to compare their performance.
Comparator Operations
A comparator consists of a single operation that enables you to compare two objects for relative order. It returns a negative integer, zero, or a positive integer, depending on whether the first argument is less than, equal to, or greater than the second, respectively. It throws a ClassCastException if the type of either object prevents them from being compared.
The Comparator Interface
A comparator is very simple — it has a single method that enables you to compare two objects to determine whether the first object is less than, equal to, or greater than the second object. The following code shows the Comparator interface:
public interface Comparator {
public int compare(Object left, Object right);
}
The compare operation takes two arguments: left and right. We have chosen to label them as such because, in this context, they are conceptually rather like the left-side and right-side arguments when comparing primitive values. When calling compare, if left comes before right (left < right), the result is an integer less than zero (usually –1); if left comes after right (left > right), the result is an integer greater than zero (usually 1); and if left equals right, the result of the comparison is zero.
Some Standard Comparators
In addition to the many custom comparators you will create, there are also a few standard comparators that will greatly simplify your application code. Each one is simple in concept and implementation yet quite powerful when used with some of the more complex algorithms discussed later in the book.
Working with the Natural Comparator
Many data types, especially primitives such as strings, integers, and so on, have a natural sort order: A comes before B, B comes before C, and so on. A natural comparator is simply a comparator that supports this natural ordering of objects. You will see that it is possible to create a single comparator that can sort any object that has a natural sorting order by basing it on a convention established by the Java language itself. Java has the concept of Comparable — an interface that can be implemented by any class you are using to provide a natural sort order.
117

Chapter 6
The Comparable Interface
The Comparable interface is simple, consisting of the single method shown here:
public interface Comparable {
public int compareTo(Object other);
}
Similar to a Comparator, it returns a negative integer, a positive integer, or zero to indicate that one object comes before, after, or is equal to another, respectively. The difference between a Comparator and a Comparable object is that a Comparator compares two objects with each other, whereas a Comparable object compares another object with itself.
Sometimes you may want to have your own classes implement Comparable to give them a natural sort order. A Person class, for example, may be defined as sorting by name. The fact that this concept is reflected in the standard Java language enables you to create a generic Comparator for sorting based on the natural ordering of a type. You can create a Comparator that will work for any class that implements Comparable. The fact that many of the commonly used classes in the java.lang package implement this interface makes it a handy comparator to start with.
When you think about the desired behavior of the NaturalComparator, you can see that there are three possible scenarios to handle, one for each of the three possible types of comparison result. You already know that strings in Java implement Comparable, so you can use strings as test data. In the next Try It Out, you test and then implement the NaturalComparator.
Try It Out |
Testing the Natural Comparator |
You first test whether a negative integer results when the left argument falls before the right when sorting:
public void testLessThan() { assertTrue(NaturalComparator.INSTANCE.compare(“A”, “B”) < 0);
}
Next, you determine whether a positive integer results when the left argument sorts after the right argument:
public void testGreaterThan() { assertTrue(NaturalComparator.INSTANCE.compare(“B”, “A”) > 0);
}
Finally, when the two arguments are equal, you determine whether the result is zero:
public void testEqualTo() { assertTrue(NaturalComparator.INSTANCE.compare(“A”, “A”) == 0);
}
How It Works
The test case contains one test method for each of the three cases we identified above. Each test method assumes that the NaturalComparator provides a single static instance that you can use without needing to instantiate it. Each test method uses two simple character strings as test data to validate that the NaturalComparator behaves as expected.
118

Basic Sorting
Try It Out |
Implementing the Natural Comparator |
Because the NaturalComparator has no state, you only need one instance of it:
public final class NaturalComparator implements Comparator { public static final NaturalComparator INSTANCE =
new NaturalComparator();
private NaturalComparator() {
}
...
}
To ensure this, you mark the constructor as private to prevent instantiation and instead provide a publicly accessible static variable holding the single instance of the class. You must also be sure to mark the class as final to prevent it from being extended erroneously.
Next you implement compare(). Because you are implementing this on top of the Comparable interface, most of the actual work will be performed by the arguments themselves, making the implementation almost trivial:
public int compare(Object left, Object right) { assert left != null : “left can’t be null”;
return ((Comparable) left).compareTo(right);
}
After first ensuring you haven’t been passed a NULL argument, you cast the left argument to a Comparable and call the defined compareTo() method, passing the right argument.
You never check to see whether the left argument is actually an instance of Comparable because the Comparator interface specifically allows a ClassCastException to be thrown, meaning you can perform the cast without the additional check.
How It Works
The NaturalComparator is designed to compare two objects that implement the Comparable interface. Many built-in Java objects implement this interface, and classes you create are free to implement it as well. The code only needs to cast the left operand to the Comparable interface so that it can call the compareTo() method, passing in the right operand for the comparison to be performed by the left operand itself. The comparator here is not actually required to implement any comparison logic because it is all handled by the objects themselves.
Working with the Reverse Comparator
Often, you will want to sort things in reverse order. For example, when looking at a list of files on your computer, you may want to see the files from smallest to largest, or in reverse order from largest to smallest. One way to achieve a reverse version of the NaturalComparator described previously is to copy its implementation and reimplement the compare() method, as shown here:
public int compare(Object left, Object right) { assert right != null : “right can’t be null”;
return ((Comparable) right).compareTo(left);
}
119

Chapter 6
You swap the right and left arguments, confirming that the right argument is not null and then passing the left argument to its compare() method.
Although this approach works perfectly well in this particular case, it isn’t very extensible. For each complex type, such as Person or File, you always end up creating two comparators: one to sort ascending, and one to sort descending.
A better approach, which you take in the next Try It Out, is to create a generic comparator that wraps (or “decorates”) another comparator and reverse the result. This way, you only need one comparator for each complex type you wish to sort. You use the generic ReverseComparator to sort in the opposite direction.
Try It Out |
Testing the Reverse Comparator |
As with NaturalComparator, there are three possible scenarios to handle, matching the three possible types of comparison result. For these tests, you use the previously defined NaturalComparator to enable you to compare simple string values.
If the left argument would normally sort before the right, you want the ReverseComparator to cause the opposite to occur; that is, if the underlying comparator returns a negative integer, indicating
that the left argument is less than the right argument, you need to ensure that the result from the ReverseComparator is a positive integer:
public void testLessThanBecomesGreaterThan() { ReverseComparator comparator =
new ReverseComparator(NaturalComparator.INSTANCE);
assertTrue(comparator.compare(“A”, “B”) > 0);
}
If the underlying comparator returns a positive integer, indicating that the left argument would normally sort after the right, the result should be a negative integer:
public void testGreaterThanBecomesLessThan() { ReverseComparator comparator =
new ReverseComparator(NaturalComparator.INSTANCE);
assertTrue(comparator.compare(“B”, “A”) < 0);
}
If the two arguments are equal, then the result must be zero:
public void testEqualsRemainsUnchanged() { ReverseComparator comparator =
new ReverseComparator(NaturalComparator.INSTANCE);
assertTrue(comparator.compare(“A”, “A”) == 0);
}
120

Basic Sorting
How It Works
The preceding code works by instantiating ReverseComparator objects and passing to them a NaturalComparator to which the comparison logic can be delegated. The first two test methods then make what look like nonsensical assertions: You know that A comes before B, but the opposite is true in this case, and the first test method makes sure this is the case. The second test method is similarly counterintuitive. The final test method ensures that objects that are equal remain equal when the
ReverseComparator is used.
In the following Try It Out, you implement your ReverseComparator.
Try It Out |
Implementing the Reverse Comparator |
Implement the generic ReverseComparator with a few lines of code:
package com.wrox.algorithms.sorting;
public class ReverseComparator implements Comparator { private final Comparator _comparator;
public ReverseComparator(Comparator comparator) {
assert comparator != null : “comparator can’t be null”; _comparator = comparator;
}
...
}
You start, of course, by implementing the Comparator interface and defining a constructor that accepts the underlying Comparator to which you will eventually delegate the compare call.
Then comes the actual implementation of compare:
public int compare(Object left, Object right) { return _comparator.compare(right, left);
}
How It Works
At first glance, the code looks rather innocuous, simply delegating to the underlying comparator, but if you look carefully at the code, you will see that the two arguments are reversed before you pass them. If the ReverseComparator was called with (A, B), then the underlying comparator would be passed (B, A), thereby inducing the opposite result.
Because you don’t actually need to access any of the attributes for either argument, this solution is completely generic; you need only implement it once to have a solution for all situations. You can now start to build your first sorting algorithm, the bubble sort algorithm.
Understanding Bubble Sort
Before implementing the bubble sort algorithm, you need to define some test cases for the implementation to pass. Because all of the sorting algorithms need to pass the same basic test (that is, prove that they actually sort objects correctly), you establish a base class for your unit tests to extend for each
121
Chapter 6
specific implementation. Each of the algorithms implements an interface so that they can be replaced easily. This means that you can use a single test case to prove any sorting algorithm’s basic features, even one you haven’t thought of yet!
Try It Out |
Performing a Bubble Sort |
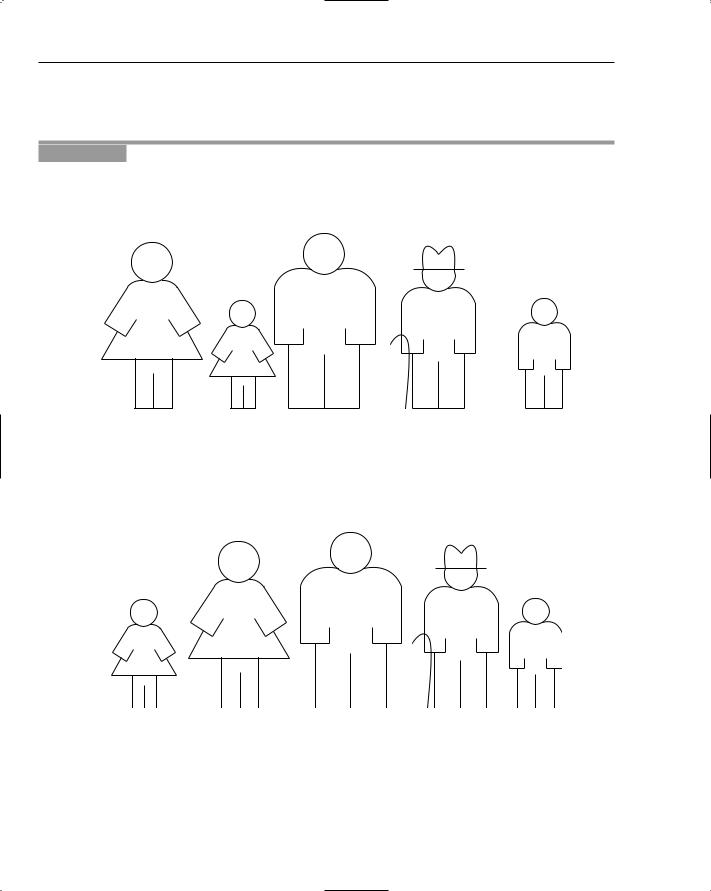
Imagine you are at a family gathering and you want to take a photograph of everyone there. You decide you’d like the family members to be arranged in age order, from youngest to oldest, but right now they’re arranged randomly, as shown in Figure 6-1.
Figure 6-1: Randomly arranged family members.
To apply a bubble sort to this problem, turn your attention to the two people at the left of the line of family members. Ask them which one is older. If the one on the right of the pair is older, then do nothing, as they are sorted relative to each other. If the one on the left is older, then ask them to swap positions. In this case, the swap needed to happen. Figure 6-2 shows the family after this first swap has taken place.
Figure 6-2: The first swap has taken place.
Now move your attention along the line one place to address the second and third people in the line. The second person has just been compared with the first person and is now about to be compared with the third person. Repeat the same procedure as before, asking them which one is older and swapping them if they are out of order.
122
Basic Sorting
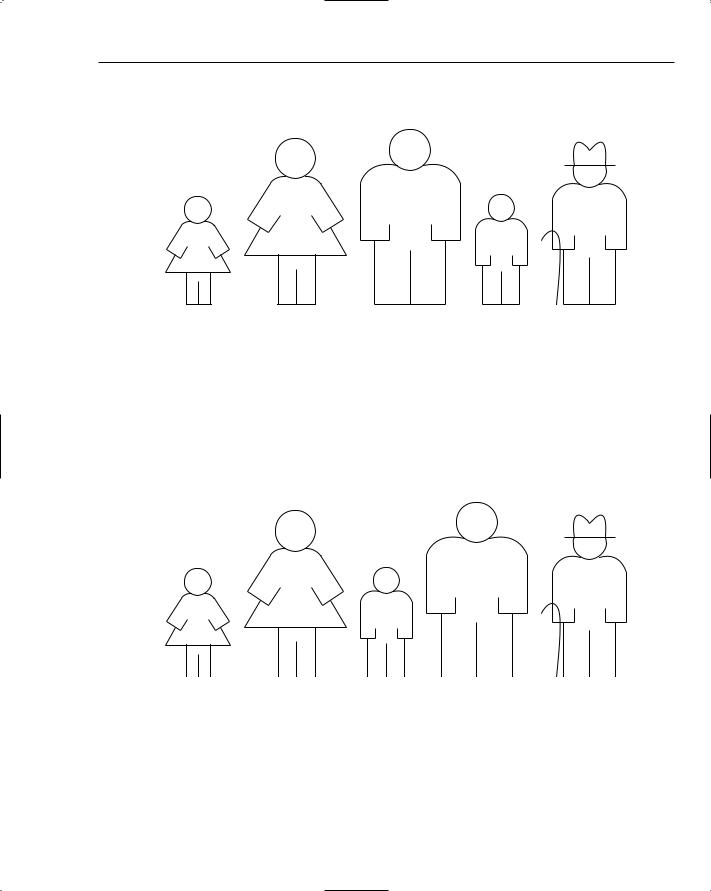
By the time you get to the last pair on the line of people and perform any necessary swaps, what will have happened? Figure 6-3 shows the family group after this first pass.
Figure 6-3: The family after the first pass — the oldest person is at the far right.
The group is by no means sorted, but the oldest person has bubbled up to the end of the line and is now in final sorted position. It probably seems like that was a lot of comparing and swapping just to get one person sorted, and that’s true. Algorithms you’ll see later have improved efficiency, but don’t worry about that for now.
The next pass in the bubble sort algorithm is exactly the same as the first except you ignore the person at the right end of the line, as that person is already sorted. Starting at the far left again, do the same compare/swap process until the second oldest person is at the second rightmost position in the line, as shown in Figure 6-4.
Figure 6-4: The second oldest person is at the second rightmost position after the second pass.
Continue in this way, gradually sorting the smaller and smaller remaining groups until the whole group is sorted. Now you can take your picture (see Figure 6-5).
123
