Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

Интегрированные системы управления и проектирования

Файл:

Сандаков Начала тензорного исчисления Методические рекомендации 2009

.pdf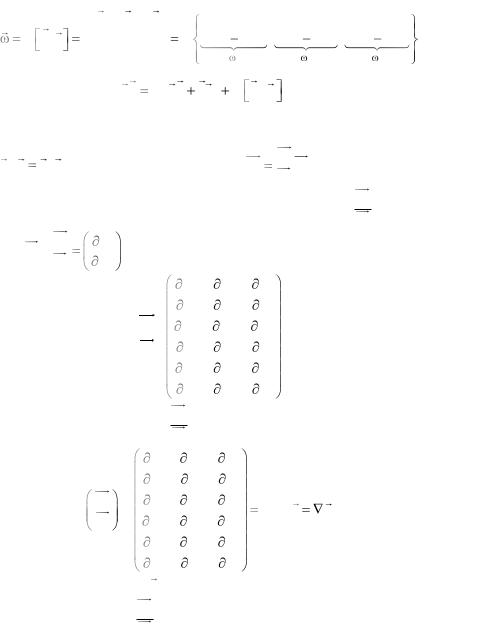

Скачиваний:

Добавлен:

17.08.2013

Размер:

1.91 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

1		1	e1	e1			e1		1
1		1	1		2			3	1		2		3		2		3	1	3	3	1	2	1	1	2
	b, a		b b			b				b		a		a		b		;a b		a b ;a			b a b			.
2	b, a	2	b b			b			2	b		a		a		b		;a b		a b ;a			b a b			.
2		2	a1	a2		a3			2					1						2				3
Таким образом,				ab			1		ab	ba				1	b, a .
Таким образом,				ab		2			ab	ba				2	b, a .
						2								2

Пример 7 (тензор относительных смещений). Рассмотрим де-

формированное состояние тела. Пусть a	– вектор смещения точки
r : a a r . Приращение вектора a : da		da	dr – тензор относи-

		dr

тельных смещений – скалярное произведение тензора da на век-

тор dr,

, его матрица:

x j

Тензор, сопряженный с da dr

		a1	a2	a3
		x1	x1	x1
da	*:	a1	a2	a3	grad a	a .
	*:	x2	x2	x2	grad a	a .
dr		x2	x2	x2
		a1	a2	a3
		x3	x3	x3

Таким образом, grad a – это тензор.

Разложим тензор da на симметричный и антисимметричный. dr

Симметричный тензор

–

тензор деформации.

Антисимметричный тензор

1 da

1 a1

1 a2

2 dr

2 x2

2 x3

где

rot a , т.е.

;

1 a2

2 x2

2 x3

2 x1

Если вектор

есть вектор смещения частиц упругого тела, то

тензор

, где D – тензор деформации;

– тензор относи-

тельного поворота.

В потенциальном поле rot a 0 , следовательно, относительные смещения происходят за счет чистой деформации. Если тело не деформируемо, то относительные смещения происходят за счет чистого поворота.

Таким образом, тензор относительных смещений

	da	da		dr	Ddr		dr Ddr	1	rot a, dr ,
	da			dr	Ddr		dr Ddr	2	rot a, dr ,
		dr						2
			e1		e2	e3
			e1		e2	e3
так как	, dr		1		2	3	dr.
			1		2	3
			dx1		dx2	dx3

§ 9. Дифференцирование тензора по скалярному аргументу

Рассмотрим случай, когда независимой переменной является скалярный аргумент, например время t. Задание тензора T (t) осу-

ществляется			или			с	помощью		задания		его		матрицы
	t1	t1	t1
	1	2	3
T (t)	t 2	t 2	t 2	,	или в диадной форме					T (t)	T e .	Убедимся в
	1	2	3								i i
	t3	t3	t3
	1	2	3
том,	что всякий тензор T						ti	можно представить в виде суммы
							k
трех диад
	t1				t1			t1		t1	0	0
	1				2			3		1
T e :	t2	1 0	0		t2	0	1 0	t2	0 0 1	t2	0	0	... ti .
i i	1				2			3		1			k
	t3				t3			t3		t3	0	0
	1				2			3		1

Заметим, что понятия непрерывности тензора, предела и т.п. могут быть введены так же, как непрерывность и предел функции.

Определение. Производной тензора T (t) по аргументу t называ-


ется lim	T (t		t)	T (t) dT			, если этот предел существует. Таким
			t			dt
t 0
образом,		dT	ti	или	dT		T e . Мы всегда будем предполагать,

		dt	k		dt		i i

что этот предел существует и непрерывен. Все основные свойства

производных функций сохраняются и для производных от тензора,

например

d T1 T2

dT1

dT2

d mT

, если m –

скалярная функция от t. Если T – тензор,

– вектор, зависящие от

t, то

d Ta

;

d T1T2

dT1

dT2

. Выведем фор-

мулу для дифференцирования обратного тензора. Если существует

такой тензор A, что AT I ( I – единичный тензор),	то тензор A
называется обратным для тензора T и обозначается	T 1. Не для

всякого тензора существует обратный тензор. Действительно, если

D A	– определитель матрицы тензора A, D T	– определитель
матрицы тензора T, то D(A)D(T ) D(I ) , а D(I )		1 , следовательно,
D(T )	должен быть отличным от нуля, т.е. тензор должен быть

полным. Полнота тензора является необходимым и достаточным условием существования обратного тензора T 1. Пусть T t – полный переменный тензор, так что определитель этого тензора

D T

0 .

Пусть

T 1 –

обратный

тензор, так

что TT 1 I .

1 T

dT 1

0 , так

как

I –

постоянный

тензор, отсюда

dT 1

Умножая обе части этого равенства слева на

T 1,

получим

T 1

1. Иногда приходится решать диф-

ференциальные уравнения, где неизвестными являются тензоры. Пример 6.

UX ,

(7)

где

X (t) – искомый тензор; U – заданный постоянный тензор. Ес-

ли

бы

мы

имели

обыкновенное дифференциальное

уравнение

(

– постоянное), то решением была бы

функция

e t

2t2

3t3

... Проверим, не будет ли сумма ряда

тензоров

X1(t)

U 2t2

U 3t3

...

решением

тензорного

уравнения (7). Обозначим X (t)

eUt ,

дифференцируем

(t) по t:

dX1

U 2t U 3t

... U I

Ut U

... UX1 (t ) , напом-

ним, что I – тензор с матрицей

. Мы показали, что функ-

ция	X1(t) eUt		удовлетворяет уравнению						dX	UX . Предполага-
									dt

лось,	что ряд	I	Ut		U 2t		2	... сходится и его можно почленно
				1!		2!

дифференцировать. Это легко доказывается. Ищем теперь общее

решение уравнения (7). Пусть

X (t) X1(t)Y (t) ,

где Y (t)

–

новая

неизвестная

функция:

dX1

но

dX1

UX1 ,

UX Y

0 ,

(t)

eUt

1 dt

имеет

обратный

тензор

e Ut ,

т.е.

является

полным,

тогда

C –

постоянный тензор. Таким образом, общим ре-

шением уравнения (7) является

X (t)

eUtC ,

где С – постоянный

тензор,

eUt определяется

рядом

X1(t)

U 2t2

U 3t3

... .

Положим в формуле

X (t)

eUtC

0 и так как

X1(0)

eU 0

I ,

получаем,

что

X (0)

C. Таким образом,

С –

начальное значение

тензора X (t) .

Замечание. Обратим внимание на

подчеркнутое

равенство

0 .

Из равенства

нулю

произведения

двух тензоров

не

следует,

что

хотя

бы

один

из

них

является

нулевым.

Действительно,						рассмотрим			тензор			A	e1e2 с матрицей:
1	0	0	0	1		0	0	1	0
0	1	0	0	0		0	0	0	0	e2 ,	A	–	ненулевой тензор,
0	0	0	0	0		0	0	0	0
	0	1		0	0	1	0	0	0	0
AA	0	0		0	0	0	0	0	0	0	– нулевой тензор. Если же в
	0	0		0	0	0	0	0	0	0

равенстве AB

0 один из тензоров является полным

det A 0 , то

другой тензор равен нулю. Получим

0 , X1

– полный тен-

U 2t2

U 3t3

зор,

X1(t) I

... ,

I –

тензор

с матрицей

0 .

§ 10. Дифференцирование тензора по координатам

Рассмотрим тензор T tki и вектор r			x1, x2 , x3 . Производ-
				ti
ной тензора T называется совокупность величин				k	(в трехмер-
ной тензора T называется совокупность величин				x j	(в трехмер-
				x j
	dT	ti
ном пространстве их будет 27).		k	. При дифференциро-
ном пространстве их будет 27).	dr	x j	. При дифференциро-

вании ранг тензора увеличивается на единицу. Для этого достаточно доказать, что при переходе к новому базису координаты тензора

k преобразуются по базисному закону. x j

Действительно, в новом базисе

cl bi

x j

k h xm

(xs )

cl chcm

i s

x j

i j

sj 1,s

ранг тензора увеличился на единицу.

(csm xs )

x j

tlh

§ 11. Приведение симметричного тензора 2-го ранга к главным осям

Будем интерпретировать аффинный ортогональный тензор как

линейный оператор	Ta b	ti	ak	bi .	Если вектор b	коллинеа-
рен вектору a , т.е.		k		после преобразования с помо-
рен вектору a , т.е.	если вектор		a	после преобразования с помо-
щью линейного оператора T изменяет только свою величину, не

изменяя направления, то направление вектора a называется глав-
ным направлением тензора T. Если b					a , то величина	называ-

ется главным значением тензора T. Оно показывает, во сколько раз тензор T увеличивает векторы, направленные по главным осям тензора, направление главных осей тензор не меняет. Найдем главные значения и главные оси тензора. Уравнение Ta a равносильно трем уравнениям:

t1a1	t1a2	t1a3	a1	t1ai
1	2	3		i
t2a1	t2a2	t2a3	a2	t 2ai
1	2	3		i
t3a1	t3a2	t3a3	a3	t3ai
1	2	3		i

a1; a2 ; a3 ,

или tk ai	ak , k 1, 2, 3. Имеем три линейных однородных урав-
i
нения относительно a1,		a2 , a3 :
	t1	a1	t1a2	t1a3	0;
	1		2	3
	t2a1	t2	a2	t2a3	0;	(8)
	1	2		3
	t3a1	t3a2	t3	a3	0,
	1	2	3

Эта система имеет ненулевое решение, если ее определитель равен нулю.

t1		t1	t1
1		2	3
t2	t2		t2	0 .
1	2		3
t3		t3	t3
1		2	3

Это уравнение называется характеристическим(вековым). Из

него определяем – главное значение тензора.	При данном из
системы (8) находим отношение a1 : a2 : a3, т.е.	главное направле-
ние тензора, отвечающее главному значению .	Если тензор сим-
метричен, т.е. если его матрица в каждом базисе	e симметрична,

то все корни характеристического уравнения вещественны. Можно так выбрать нормированные собственные векторы e1, e2 , e3, отве-

чающие собственным значениям 1, 2 , 3 , чтобы они представ-

ляли ортогональный нормированный базис (ОНБ) и в этом ОНБ матрица тензора T будет иметь диагональную форму, так как из-

вестно, что линейный оператор задается в базисе e диагональной

матрицей тогда и только тогда, когда векторы этого базиса являются собственными векторами линейного оператора.

Таким образом, в этом ОНБ все элементы тензора, кроме диагональных, обращаются в нуль и сам тензор принимает простейший

1	0	0
1

вид T	0	2	0	. Преобразование вектора b Ta имеет про-
		2
	0	0	3
			3
стой вид b1		a1,		b2	2	a2 ,	b3	3	a3. Для симметричного тен-
		1			2			3
зора направления			осей		e1, e2		, e3,	являются главными направле-
ниями, а величины				1,	2 , 3 – главными значениями. Таким обра-

зом, в случае симметричного тензора существуют три главных направления и три главных значения. Выбор базиса e , в котором

матрица тензора имеет диагональную форму, называется приведением тензора к главным осям.

Глава III. ПОЛЕ ТЕНЗОРА

§ 12. Дивергенция тензора

Если каждой точке M некоторой области D пространства ставится в соответствие тензор T ~ tik , то говорят, что в области D задано поле тензора T. Обобщим определение вектора и дадим оп-

ределение аффинного ортогонального тензора в пространстве E3 в такой же форме.

Определение. Если в каждом ОНБ дана упорядоченная совокуп-

ность трех чисел x1, x2 , x3 ,		которые при переходе к новому бази-
су преобразуются по закону		xi bi x k	или xi ck xk	(так как в
		k	i
евклидовом	пространстве bi	ck ), то	совокупность	этих чисел
	k	i
(x1, x2 , x3 )	называют аффинным ортогональным вектором x .

Введем понятие тензора, обобщив это определение. Если в каж-

дом ОНБ дана совокупность векторов T1,	T2 , T3 , которые при пе-
реходе к новому базису преобразуются по закону T			CkT , то со-
		i	i k
вокупность этих трех векторов T1, T2 , T3	называется ортогональ-
ным тензором второго ранга. Векторы T1,	T2 ,	T3 можно называть
составляющими тензора T по осям e1, e2	, e3 .	Иногда аффинные

ортогональные тензоры 2-го ранга называют аффинорами. Разло-

жим векторы T1, T2 , T3	по базису					e .
T	t1e		t	2e			t3e		tie ;
1	1	1	1		2		1	3	1	i
			T			ti e ;
			2			2	i
			T			ti e .
			3			3	i

Определим дивергенцию тензора T с составляющими T1, T2 , T3 . Предположим, что T C1(D) , т.е. tki C1(D) (координаты тензора являются функциями координат точки M (x1, x2 , x3 ) ). Дивергенцией тензора T называется вектор

div T	T1	T2	T3
div T	dx1	dx2	dx3
	dx1	dx2	dx3

div T

1 e

div T

2 e

div T 3 e

Таким образом,

div T

– вектор

e .

dxi

	t2					t3
2			e		2		e
			e				e
	x2	2				x2	3
	x2					x2
	t2					t3
	i		e			i	e
			e				e
	xi	2				xi	3
	xi					xi
				i				tk
	div T					e		i	e .
	div T					e			e .
						i			k
								xi

§ 13. Формула Гаусса – Остроградского для поля тензора

Пусть t k			– координаты тензора T, которые принадлежат классу
	i
C1 D . По аналогии с вектором тензор можно представить в виде
суммы T		T1e1		T2e2	T3e3 , т.е. в виде суммы трех диад: Tiei . Дей-
ствительно,
	t1		t1	t1	t1		0 0	0 t1	0	0 0 t1
	1		2	3	1			2			3
T	t	2	t2	t2	t2		0 0	0 t2	0	0 0 t2
	1		2	3	1			2			3
	t	3	t3	t3	t3		0 0	0 t3	0	0 0 t3
	1		2	3	1			2			3
	t1				t1			t1
	1					2		3
	t2		1 0 0		t	2	0 1 0	t2	0 0 1		ti .
	1					2		3			k
	t3				t	3		t3
	1					2		3
Определим в каждой точке поля для каждого направления n
вектор	Tn		Tn	T1 cos	n, x1		T2 cos	n, x2	T3 cos	n, x3 . Рассмот-
рим интеграл				TndS и применим к нему формулу Гаусса – Остро-
			S
градского:

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в предмете Интегрированные системы управления и проектирования