1.2. Операции с числами
Задание 1.1. Вычислите указанное арифметическое выражение. Укажите последовательность нажатия клавиша. Сравните полученный результат с приведенным ответом.
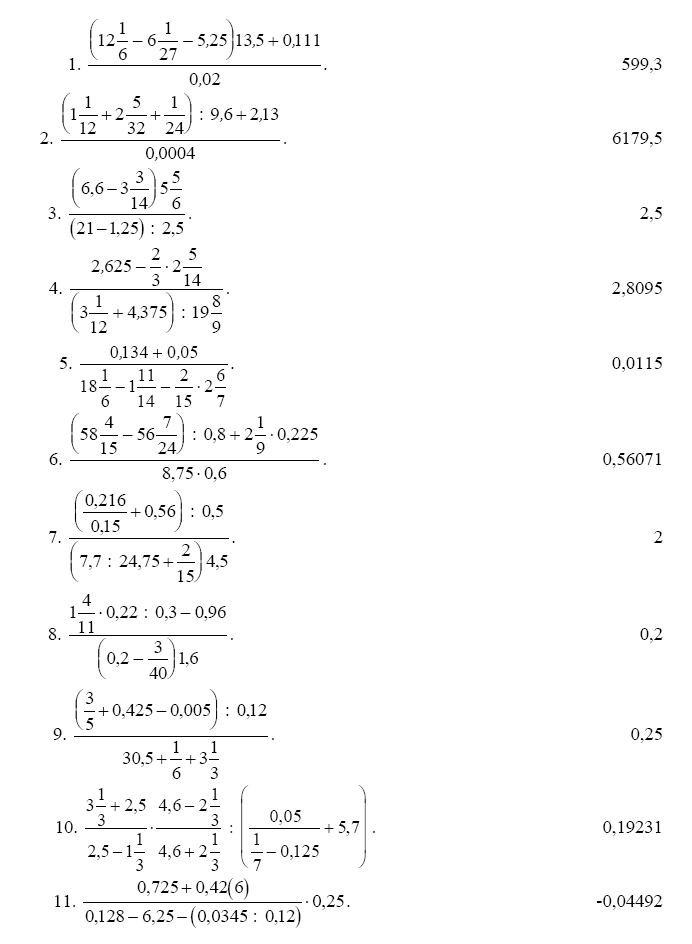
Задание 1.2. Проведите вычисления по заданной формуле при заданных значениях параметров. Укажите необходимую последовательность действий.
Сравните полученный результат с приведенным ответом.
Указание. В системе MatLAB несколько последних команд запоминаются.
Повторный вызов этих команд в командное окно осуществляется нажатием клавиш <↑ и <↓>. Используйте эту возможность для повторного обращения к набранной функции.
Задание 1.3. Выполните такие действия (см. таблицу 1.1):
а) число z1, заданное в алгебраической (экспоненциальной) форме, переведите в экспоненциальную (алгебраическую), проверьте и запишите результат;
б) число z2, заданное в экспоненциальной (алгебраической) форме, переве-
дите в алгебраическую (экспоненциальную), проверьте и запишите езультат;
в) вычислите заданное выражение; запишите результат экспоненциальной
форме, причем аргумент результата обеспечьте в границах между (-π) и +π.
Задание 1.4. Найдите корни квадратного уравнения
при заданных значениях коэффициентов a, b и c (см. таблицу 1.2).
|
Вариант |
а |
b |
c |
|
1 |
0.56 |
1.2е-4 |
4.08 |
|
2 |
1 |
0.1 |
100 |
|
3 |
4. 2e-3 |
8. 03e-4 |
1.06 |
|
4 |
7. 1e3 |
9. 4e4 |
8. 3e10 |
|
5 |
5.09 |
4.32 |
256 |
|
6 |
8.3 |
5.34 |
693 |
|
7 |
27 |
27 |
1276 |
|
8 |
3.08 |
0.2 |
30 |
|
9 |
5.3 |
10.6 |
876 |
|
10 |
0.45 |
0. 034 |
121 |
|
11 |
4.3 |
10.7 |
3. 4e3 |
|
12 |
13 |
0.8 |
287 |
|
13 |
6. 035 |
5.2 |
875 |
|
14 |
2.3 |
7.9 |
324 |
|
15 |
1 |
0.02 |
16.57 |
|
16 |
1.3 |
0.56 |
18.8 |
|
17 |
0.13 |
0. 056 |
18.8 |
|
18 |
17 |
12 |
956 |
|
19 |
0. 085 |
1 |
1. 3e3 |
|
20 |
1.2 |
0.32 |
15 |
|
21 |
7.1 |
6.4 |
256 |
|
22 |
0.2 |
0. 002 |
2.9 |
|
23 |
1. 4e-3 |
3.9 |
2. 6e2 |
|
24 |
0.86 |
3.2 |
5. 4e2 |
|
25 |
7. 3e3 |
8. 2e2 |
3. 5e8 |
1.3. Простейшие операции с векторами и матрицами
Задание 1.5. Вычислите значения функции f(x) на отрезке [a; b] с шагом h.
1.4. Функции прикладной численной математики
Задание 1.6.
1. Введите произвольную матрицу размером (4*6). Найдите сумму наибольших элементов ее строк.
2. Введите квадратную матрицу (5*5) с одним наименьшим элементом. Найдите сумму элементов строки, в которой размещен элемент с наименьшим значением.
3. Введите матрицу (6*9), в которой есть единственные наибольший и наименьшие элементы и они расположены в разных строках. Поменяйте местами строку с наибольшим элементом и строку с наименьшим элементом.
4. Введите матрицу (5*6) с разными значениями элементов. В каждой строке выберите элемент с наименьшим значением, из полученных чисел выберите наибольшее. Найдите индексы полученных элементов.
5. Введите матрицу (5*6). Найдите вектор, элементами которого являются наибольшие элементы соответствующей строки матрицы.
6. Введите матрицу (5*6). Постройте вектор, элементами которого являются суммы наибольшего и наименьшего элементов соответствующей строки матрицы.
7. Введите матрицу (5*6). Постройте вектор, элементами которого являются средние значения элементов соответствующей строки матрицы.
8. Введите матрицу (5*6). Постройте вектор, элементами которого являются среднеквадратичные отклонения элементов соответствующей строки матрицы от их среднего значения.
9. Введите матрицу (5*6). Постройте вектор, элементами которого являются средние арифметические наибольшего и наименьшего элементов соответствующей строки матрицы.
10. Введите матрицу (6*5). Постройте вектор, элементами которого являются суммы квадратов элементов соответствующего столбца матрицы.
11. Введите матрицу (5*5). Постройте векторы, элементами которых являются суммы элементов столбцов матрицы, произведения элементов столбцов и наименьшие значения элементов столбцов.
12. Введите матрицу (5*6). Найдите среднее арифметическое наибольших и наименьших ее элементов.
13. Введите матрицу (5*5). Постройте вектор, элементами которого являются элементы главной диагонали матрицы. Найдите след матрицы.
14. Введите две матрицы (4*4). Постройте новую матрицу размером (4*8), включая в первые 4 столбца строки первой матрицы, а в другие – столбцы второй матрицы.
15. Найдите сумму всех элементов матрицы размером (4*3).
Задание 1.7. Вычислите векторы:
а) модуля частотной передаточной функции (ЧПФ);
б) аргумента ЧПФ;
в) действительной части ЧПФ;
г) мнимой части ЧПФ по заданным числителю и знаменателю передаточной функции (табл).
Предварительно найдите корни знаменателя передаточной функции, определите наибольшую собственную частоту ωmax системы. Обеспечьте вычисление ЧПФ при 100 значениях частоты ω в диапазоне от 0 до 5ωmax .
Указание. Частотной передаточной функцией называют передаточную
функцию системы при мнимых значениях аргумента (p= j⋅ω ).
Собственные частоты системы - это значения модулей мнимых частей
корней характеристического уравнения системы (которое получается приравниванием нулю знаменателя передаточной функции).
Задача 1.8. Введите произвольную матрицу размером (5*5). Найдите:
1) определитель матрицы; в случае, если определитель окажется равным нулю, или слишком малым, измените некоторые элементы матрицы и повторите вычисления;
2) обратную матрицу; проверьте правильность путем обращения обратной матрицы;
3) характеристический полином матрицы;
4) корни характеристического полинома матрицы; рассортируйте корни по комплексно-спряженным парам и в порядке возрастания величин;
5) собственные значения матрицы; сравните с ранее найденными корнями характеристического полинома;
6) LU-разложение матрицы; проверьте его правильность;
7) QR-разложение матрицы; проверьте его правильность;
8) сингулярные числа матрицы; сравните их с получаемыми при svd-
разложении;
9) след матрицы;
10) число обусловленности матрицы;
11) экспоненту от матрицы;
12) логарифм от экспоненты матрицы; сравните с исходной матрицей.