
матан коллоквиум / 9.Производная параметрической неявной функции,правило Лапиталя
..docxПроизводная функции, заданной неявно. Производная параметрически заданной функции
В данной статье мы рассмотрим еще два типовых задания, которые часто встречаются в контрольных работах по высшей математике. Для того чтобы успешно освоить материал, необходимо уметь находить производные хотя бы на среднем уровне. Научиться находить производные практически с нуля можно на двух базовых уроках Как найти производную? Примеры решений и Производная сложной функции. Если с навыками дифференцирования всё в порядке, тогда поехали.
Производная функции, заданной неявно
Или короче – производная неявной функции. Что такое неявная функция? Поскольку мои уроки носят практическую направленность, я стараюсь избегать определений, формулировок теорем, но здесь это будет уместно сделать. А что такое вообще функция?
Функция
одной переменной ![]() – это
правило, по которому каждому значению
независимой переменной
– это
правило, по которому каждому значению
независимой переменной ![]() соответствует
одно и только одно значение функции
соответствует
одно и только одно значение функции ![]() .
.
Переменная ![]() называется независимой
переменной или аргументом.
Переменная
называется независимой
переменной или аргументом.
Переменная ![]() называется зависимой
переменной или функцией.
называется зависимой
переменной или функцией.
Грубо говоря, буковка «игрек» в данном случае – и есть функция.
До сих пор мы рассматривали функции, заданные в явном виде. Что это значит? Устроим разбор полётов на конкретных примерах.
Рассмотрим
функцию ![]()
Мы
видим, что слева у нас одинокий «игрек»
(функция), а справа – только
«иксы».
То есть, функция ![]() в
явном виде выражена
через независимую переменную
в
явном виде выражена
через независимую переменную ![]() .
.
Рассмотрим
другую функцию: ![]()
Здесь
переменные ![]() и
и ![]() расположены
«вперемешку». Причем никакими
способами невозможно выразить
«игрек» только через «икс». Что это за
способы? Перенос слагаемых из части в
часть со сменой знака, вынесение за
скобки, перекидывание множителей по
правилу пропорции и др. Перепишите
равенство
расположены
«вперемешку». Причем никакими
способами невозможно выразить
«игрек» только через «икс». Что это за
способы? Перенос слагаемых из части в
часть со сменой знака, вынесение за
скобки, перекидывание множителей по
правилу пропорции и др. Перепишите
равенство ![]() и
попробуйте выразить «игрек» в явном
виде:
и
попробуйте выразить «игрек» в явном
виде: ![]() .
Можно крутить-вертеть уравнение часами,
но у вас этого не получится.
.
Можно крутить-вертеть уравнение часами,
но у вас этого не получится.
Разрешите
познакомить: ![]() –
пример неявной
функции.
–
пример неявной
функции.
Правило
Бернулли-Лопита́ля —
метод нахождения пределов
функций, раскрывающий
неопределённости вида ![]() и
и ![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения ихпроизводных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения ихпроизводных.
Точная формулировка
Условия:
-
 либо
либо  ;
; -
 и
и  дифференцируемы
в проколотой окрестности
дифференцируемы
в проколотой окрестности  ;
; -
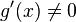 в
проколотой окрестности
в
проколотой окрестности  ;
; -
существует
 ,
,
тогда
существует ![]() .
.
Пределы также могут быть односторонними.
Доказательство
[править]Отношение бесконечно малых
Докажем
теорему для случая, когда пределы функций
равны нулю (то есть неопределённость
вида ![]() ).
).
Поскольку
мы рассматриваем функции ![]() и
и ![]() только
в правой проколотой полуокрестности
точки
только
в правой проколотой полуокрестности
точки ![]() ,
мы можем непрерывным
образом их
доопределить в этой точке: пусть
,
мы можем непрерывным
образом их
доопределить в этой точке: пусть ![]() .
Возьмём некоторый
.
Возьмём некоторый ![]() из
рассматриваемой полуокрестности и
применим к отрезку
из
рассматриваемой полуокрестности и
применим к отрезку ![]() теорему
Коши.
По этой теореме получим:
теорему
Коши.
По этой теореме получим:
![]() ,
,
но ![]() ,
поэтому
,
поэтому ![]() .
.
Дальше,
записав определение предела отношения производных и
обозначив последний через ![]() ,
из полученного равенства выводим:
,
из полученного равенства выводим:
 для
конечного предела и
для
конечного предела и
 для
бесконечного,
для
бесконечного,
что является определением предела отношения функций.
[править]Отношение бесконечно больших
Докажем
теорему для неопределённостей вида ![]() .
.
Пусть,
для начала, предел отношения производных
конечен и равен ![]() .
Тогда, при стремлении
.
Тогда, при стремлении ![]() к
к ![]() справа,
это отношение можно записать как
справа,
это отношение можно записать как ![]() ,
где
,
где ![]() — O(1).
Запишем это условие:
— O(1).
Запишем это условие:
![]() .
.
Зафиксируем ![]() из
отрезка
из
отрезка ![]() и
применим теорему
Коши ко
всем
и
применим теорему
Коши ко
всем ![]() из
отрезка
из
отрезка ![]() :
:
![]() ,
что можно привести к следующему виду:
,
что можно привести к следующему виду:
 .
.
Для ![]() ,
достаточно близких к
,
достаточно близких к ![]() ,
выражение имеет смысл; предел первого
множителя правой части равен единице
(так как
,
выражение имеет смысл; предел первого
множителя правой части равен единице
(так как ![]() и
и ![]() — константы,
а
— константы,
а ![]() и
и ![]() стремятся
к бесконечности). Значит, этот множитель
равен
стремятся
к бесконечности). Значит, этот множитель
равен ![]() ,
где
,
где ![]() —
бесконечно малая функция при
стремлении
—
бесконечно малая функция при
стремлении ![]() к
к ![]() справа.
Выпишем определение этого факта,
используя то же значение
справа.
Выпишем определение этого факта,
используя то же значение ![]() ,
что и в определении для
,
что и в определении для ![]() :
:
![]() .
.
Получили,
что отношение функций представимо в
виде ![]() ,
и
,
и  .
По любому данному
.
По любому данному ![]() можно
найти такое
можно
найти такое ![]() ,
чтобы модуль разности отношения функций
и
,
чтобы модуль разности отношения функций
и ![]() был
меньше
был
меньше ![]() ,
значит, предел отношения функций
действительно равен
,
значит, предел отношения функций
действительно равен ![]() .
.
Если
же предел ![]() бесконечен
(допустим, он равен плюс бесконечности),
то
бесконечен
(допустим, он равен плюс бесконечности),
то
![]() .
.
В
определении ![]() будем
брать
будем
брать ![]() ;
первый множитель правой части будет
больше 1/2 при
;
первый множитель правой части будет
больше 1/2 при ![]() ,
достаточно близких к
,
достаточно близких к ![]() ,
а тогда
,
а тогда  .
.
Для других баз доказательства аналогичны приведённым.
